High School Math 2011 Algebra 1(prentice Hall) Student Edition
High School Math 2011 Algebra 1(prentice Hall) Student Edition
11th Edition
ISBN: 9780133500400
Author: Prentice Hall
Publisher: Prentice Hall
bartleby

Videos

Question
Book Icon
Chapter 1.7, Problem 56PPE
To determine

To find: whether the functions f (x) and g(x) are identical are not

Expert Solution & Answer
Check Mark

Answer to Problem 56PPE

Not identical

Explanation of Solution

In order to compare f (x) and g(x), plot the graph of g(x) with given values and then compare the two graphs.

    Values of xValues of g(x)
    -11
    0-1
    1-3
    2-5
    3-7

After the values are plotted the graph of g(x) can be obtained.

Graph:

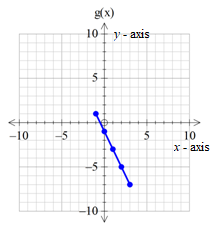
  High School Math 2011 Algebra 1(prentice Hall) Student Edition, Chapter 1.7, Problem 56PPE

Interpretation:

On comparing the graph of f (x) with g(x), it is clear that both the graphs are different.

Hence, the functions f (x) and g(x) are not identical.

Conclusion:

Therefore, given functions are not identical.

Previous
Chapter 1.7, Problem 55PPE
Next
Chapter 1.7, Problem 57PPE

Chapter 1 Solutions

High School Math 2011 Algebra 1(prentice Hall) Student Edition

Ch. 1.1 - Prob. 1PCh. 1.1 - Prob. 2PCh. 1.1 - Prob. 3PCh. 1.1 - Prob. 4PCh. 1.1 - Prob. 5PCh. 1.1 - Prob. 1LCCh. 1.1 - Prob. 2LCCh. 1.1 - Prob. 3LCCh. 1.1 - Prob. 4LCCh. 1.1 - Prob. 5LC
Ch. 1.1 - Prob. 6LCCh. 1.1 - Prob. 7LCCh. 1.1 - Prob. 8LCCh. 1.1 - Prob. 9PPECh. 1.1 - Prob. 10PPECh. 1.1 - Prob. 11PPECh. 1.1 - Prob. 12PPECh. 1.1 - Prob. 13PPECh. 1.1 - Prob. 14PPECh. 1.1 - Prob. 15PPECh. 1.1 - Prob. 16PPECh. 1.1 - Prob. 17PPECh. 1.1 - Prob. 18PPECh. 1.1 - Prob. 19PPECh. 1.1 - Prob. 20PPECh. 1.1 - Prob. 21PPECh. 1.1 - Prob. 22PPECh. 1.1 - Prob. 23PPECh. 1.1 - Prob. 24PPECh. 1.1 - Prob. 25PPECh. 1.1 - Prob. 26PPECh. 1.1 - Prob. 27PPECh. 1.1 - Prob. 28PPECh. 1.1 - Prob. 29PPECh. 1.1 - Prob. 30PPECh. 1.1 - Prob. 31PPECh. 1.1 - Prob. 32PPECh. 1.1 - Prob. 33PPECh. 1.1 - Prob. 34PPECh. 1.1 - Prob. 35PPECh. 1.1 - Prob. 36PPECh. 1.1 - Prob. 37PPECh. 1.1 - Prob. 38PPECh. 1.1 - Prob. 39PPECh. 1.1 - Prob. 40PPECh. 1.1 - Prob. 41PPECh. 1.1 - Prob. 1MPCh. 1.2 - Prob. 1PCh. 1.2 - Prob. 2PCh. 1.2 - Prob. 3PCh. 1.2 - Prob. 4PCh. 1.2 - Prob. 1LCCh. 1.2 - Prob. 2LCCh. 1.2 - Prob. 3LCCh. 1.2 - Prob. 4LCCh. 1.2 - Prob. 5LCCh. 1.2 - Prob. 6LCCh. 1.2 - Prob. 7LCCh. 1.2 - Prob. 8LCCh. 1.2 - Prob. 9PPECh. 1.2 - Prob. 10PPECh. 1.2 - Prob. 11PPECh. 1.2 - Prob. 12PPECh. 1.2 - Prob. 13PPECh. 1.2 - Prob. 14PPECh. 1.2 - Prob. 15PPECh. 1.2 - Prob. 16PPECh. 1.2 - Prob. 17PPECh. 1.2 - Prob. 18PPECh. 1.2 - Prob. 19PPECh. 1.2 - Prob. 20PPECh. 1.2 - Prob. 21PPECh. 1.2 - Prob. 22PPECh. 1.2 - Prob. 23PPECh. 1.2 - Prob. 24PPECh. 1.2 - Prob. 25PPECh. 1.2 - Prob. 26PPECh. 1.2 - Prob. 27PPECh. 1.2 - Prob. 28PPECh. 1.2 - Prob. 29PPECh. 1.2 - Prob. 30PPECh. 1.2 - Prob. 31PPECh. 1.2 - Prob. 32PPECh. 1.2 - Prob. 33PPECh. 1.2 - Prob. 34PPECh. 1.2 - Prob. 35PPECh. 1.2 - Prob. 36PPECh. 1.2 - Prob. 37PPECh. 1.2 - Prob. 38PPECh. 1.2 - Prob. 39PPECh. 1.2 - Prob. 40PPECh. 1.2 - Prob. 41PPECh. 1.2 - Prob. 42PPECh. 1.2 - Prob. 43PPECh. 1.2 - Prob. 44PPECh. 1.2 - Prob. 45PPECh. 1.2 - Prob. 46PPECh. 1.2 - Prob. 47PPECh. 1.2 - Prob. 48PPECh. 1.2 - Prob. 49PPECh. 1.2 - Prob. 50PPECh. 1.2 - Prob. 51PPECh. 1.2 - Prob. 52PPECh. 1.2 - Prob. 53PPECh. 1.2 - Prob. 54PPECh. 1.2 - Prob. 55PPECh. 1.2 - Prob. 56PPECh. 1.2 - Prob. 57PPECh. 1.2 - Prob. 58PPECh. 1.2 - Prob. 59PPECh. 1.2 - Prob. 60PPECh. 1.2 - Prob. 61STPCh. 1.2 - Prob. 62STPCh. 1.2 - Prob. 63STPCh. 1.2 - Prob. 64STPCh. 1.2 - Prob. 65MRCh. 1.2 - Prob. 66MRCh. 1.2 - Prob. 67MRCh. 1.2 - Prob. 68MRCh. 1.2 - Prob. 69MRCh. 1.2 - Prob. 70MRCh. 1.2 - Prob. 71MRCh. 1.2 - Prob. 72MRCh. 1.2 - Prob. 73MRCh. 1.2 - Prob. 74MRCh. 1.2 - Prob. 75MRCh. 1.2 - Prob. 76MRCh. 1.2 - Prob. 77MRCh. 1.2 - Prob. 78MRCh. 1.2 - Prob. 79MRCh. 1.2 - Prob. 80MRCh. 1.3 - Prob. 1PCh. 1.3 - Prob. 2PCh. 1.3 - Prob. 3PCh. 1.3 - Prob. 4PCh. 1.3 - Prob. 5PCh. 1.3 - Prob. 1LCCh. 1.3 - Prob. 2LCCh. 1.3 - Prob. 3LCCh. 1.3 - Prob. 4LCCh. 1.3 - Prob. 5LCCh. 1.3 - Prob. 6LCCh. 1.3 - Prob. 7LCCh. 1.3 - Prob. 8LCCh. 1.3 - Prob. 9PPECh. 1.3 - Prob. 10PPECh. 1.3 - Prob. 11PPECh. 1.3 - Prob. 12PPECh. 1.3 - Prob. 13PPECh. 1.3 - Prob. 14PPECh. 1.3 - Prob. 15PPECh. 1.3 - Prob. 16PPECh. 1.3 - Prob. 17PPECh. 1.3 - Prob. 18PPECh. 1.3 - Prob. 19PPECh. 1.3 - Prob. 20PPECh. 1.3 - Prob. 21PPECh. 1.3 - Prob. 22PPECh. 1.3 - Prob. 23PPECh. 1.3 - Prob. 24PPECh. 1.3 - Prob. 25PPECh. 1.3 - Prob. 26PPECh. 1.3 - Prob. 27PPECh. 1.3 - Prob. 28PPECh. 1.3 - Prob. 29PPECh. 1.3 - Prob. 30PPECh. 1.3 - Prob. 31PPECh. 1.3 - Prob. 32PPECh. 1.3 - Prob. 33PPECh. 1.3 - Prob. 34PPECh. 1.3 - Prob. 35PPECh. 1.3 - Prob. 36PPECh. 1.3 - Prob. 37PPECh. 1.3 - Prob. 38PPECh. 1.3 - Prob. 39PPECh. 1.3 - Prob. 40PPECh. 1.3 - Prob. 41PPECh. 1.3 - Prob. 42PPECh. 1.3 - Prob. 43PPECh. 1.3 - Prob. 44PPECh. 1.3 - Prob. 45PPECh. 1.3 - Prob. 46PPECh. 1.3 - Prob. 47PPECh. 1.3 - Prob. 48PPECh. 1.3 - Prob. 49PPECh. 1.3 - Prob. 50PPECh. 1.3 - Prob. 51PPECh. 1.3 - Prob. 52PPECh. 1.3 - Prob. 53PPECh. 1.3 - Prob. 54PPECh. 1.3 - Prob. 55PPECh. 1.3 - Prob. 56PPECh. 1.3 - Prob. 57PPECh. 1.3 - Prob. 58PPECh. 1.3 - Prob. 59PPECh. 1.3 - Prob. 60PPECh. 1.3 - Prob. 61PPECh. 1.3 - Prob. 62PPECh. 1.3 - Prob. 63PPECh. 1.3 - Prob. 64PPECh. 1.3 - Prob. 65PPECh. 1.3 - Prob. 66PPECh. 1.3 - Prob. 67PPECh. 1.3 - Prob. 68PPECh. 1.3 - Prob. 69PPECh. 1.3 - Prob. 70PPECh. 1.3 - Prob. 71PPECh. 1.3 - Prob. 72STPCh. 1.3 - Prob. 73STPCh. 1.3 - Prob. 74STPCh. 1.3 - Prob. 75MRCh. 1.3 - Prob. 76MRCh. 1.3 - Prob. 77MRCh. 1.3 - Prob. 78MRCh. 1.3 - Prob. 79MRCh. 1.3 - Prob. 80MRCh. 1.3 - Prob. 81MRCh. 1.3 - Prob. 82MRCh. 1.3 - Prob. 83MRCh. 1.3 - Prob. 84MRCh. 1.3 - Prob. 85MRCh. 1.4 - Prob. 1PCh. 1.4 - Prob. 2PCh. 1.4 - Prob. 3PCh. 1.4 - Prob. 4PCh. 1.4 - Prob. 1LCCh. 1.4 - Prob. 2LCCh. 1.4 - Prob. 3LCCh. 1.4 - Prob. 4LCCh. 1.4 - Prob. 5LCCh. 1.4 - Prob. 6LCCh. 1.4 - Prob. 7PPECh. 1.4 - Prob. 8PPECh. 1.4 - Prob. 9PPECh. 1.4 - Prob. 10PPECh. 1.4 - Prob. 11PPECh. 1.4 - Prob. 12PPECh. 1.4 - Prob. 13PPECh. 1.4 - Prob. 14PPECh. 1.4 - Prob. 15PPECh. 1.4 - Prob. 16PPECh. 1.4 - Prob. 17PPECh. 1.4 - Prob. 18PPECh. 1.4 - Prob. 19PPECh. 1.4 - Prob. 20PPECh. 1.4 - Prob. 21PPECh. 1.4 - Prob. 22PPECh. 1.4 - Prob. 23PPECh. 1.4 - Prob. 24PPECh. 1.4 - Prob. 25PPECh. 1.4 - Prob. 26PPECh. 1.4 - Prob. 27PPECh. 1.4 - Prob. 28PPECh. 1.4 - Prob. 29PPECh. 1.4 - Prob. 30PPECh. 1.4 - Prob. 31PPECh. 1.4 - Prob. 32PPECh. 1.4 - Prob. 33PPECh. 1.4 - Prob. 34PPECh. 1.4 - Prob. 35PPECh. 1.4 - Prob. 36PPECh. 1.4 - Prob. 37PPECh. 1.4 - Prob. 38PPECh. 1.4 - Prob. 39PPECh. 1.4 - Prob. 40PPECh. 1.4 - Prob. 41PPECh. 1.4 - Prob. 42PPECh. 1.4 - Prob. 43PPECh. 1.4 - Prob. 44PPECh. 1.4 - Prob. 45PPECh. 1.4 - Prob. 46PPECh. 1.4 - Prob. 47PPECh. 1.4 - Prob. 48PPECh. 1.4 - Prob. 49PPECh. 1.4 - Prob. 50PPECh. 1.4 - Prob. 51PPECh. 1.4 - Prob. 52PPECh. 1.4 - Prob. 53PPECh. 1.4 - Prob. 54PPECh. 1.4 - Prob. 55PPECh. 1.4 - Prob. 56PPECh. 1.4 - Prob. 57PPECh. 1.4 - Prob. 58STPCh. 1.4 - Prob. 59STPCh. 1.4 - Prob. 60STPCh. 1.4 - Prob. 61STPCh. 1.4 - Prob. 62RECh. 1.4 - Prob. 63RECh. 1.4 - Prob. 64RECh. 1.4 - Prob. 65RECh. 1.4 - Prob. 66RECh. 1.4 - Prob. 67RECh. 1.4 - Prob. 68RECh. 1.4 - Prob. 1MCQCh. 1.4 - Prob. 2MCQCh. 1.4 - Prob. 3MCQCh. 1.4 - Prob. 4MCQCh. 1.4 - Prob. 5MCQCh. 1.4 - Prob. 6MCQCh. 1.4 - Prob. 7MCQCh. 1.4 - Prob. 8MCQCh. 1.4 - Prob. 9MCQCh. 1.4 - Prob. 10MCQCh. 1.4 - Prob. 11MCQCh. 1.4 - Prob. 12MCQCh. 1.4 - Prob. 13MCQCh. 1.4 - Prob. 14MCQCh. 1.4 - Prob. 15MCQCh. 1.4 - Prob. 16MCQCh. 1.4 - Prob. 17MCQCh. 1.4 - Prob. 18MCQCh. 1.4 - Prob. 19MCQCh. 1.5 - Prob. 1PCh. 1.5 - Prob. 2PCh. 1.5 - Prob. 3PCh. 1.5 - Prob. 4PCh. 1.5 - Prob. 1LCCh. 1.5 - Prob. 2LCCh. 1.5 - Prob. 3LCCh. 1.5 - Prob. 4LCCh. 1.5 - Prob. 5LCCh. 1.5 - Prob. 6LCCh. 1.5 - Prob. 7LCCh. 1.5 - Prob. 8LCCh. 1.5 - Prob. 9LCCh. 1.5 - Prob. 10PPECh. 1.5 - Prob. 11PPECh. 1.5 - Prob. 12PPECh. 1.5 - Prob. 13PPECh. 1.5 - Prob. 14PPECh. 1.5 - Prob. 15PPECh. 1.5 - Prob. 16PPECh. 1.5 - Prob. 17PPECh. 1.5 - Prob. 18PPECh. 1.5 - Prob. 19PPECh. 1.5 - Prob. 20PPECh. 1.5 - Prob. 21PPECh. 1.5 - Prob. 22PPECh. 1.5 - Prob. 23PPECh. 1.5 - Prob. 24PPECh. 1.5 - Prob. 25PPECh. 1.5 - Prob. 26PPECh. 1.5 - Prob. 27PPECh. 1.5 - Prob. 28PPECh. 1.5 - Prob. 29PPECh. 1.5 - Prob. 30PPECh. 1.5 - Prob. 31PPECh. 1.5 - Prob. 32PPECh. 1.5 - Prob. 33PPECh. 1.5 - Prob. 34PPECh. 1.5 - Prob. 35PPECh. 1.5 - Prob. 36PPECh. 1.5 - Prob. 37PPECh. 1.5 - Prob. 38PPECh. 1.5 - Prob. 39PPECh. 1.5 - Prob. 40PPECh. 1.5 - Prob. 41PPECh. 1.5 - Prob. 42PPECh. 1.5 - Prob. 43PPECh. 1.5 - Prob. 44PPECh. 1.5 - Prob. 45PPECh. 1.5 - Prob. 46PPECh. 1.5 - Prob. 47PPECh. 1.5 - Prob. 48PPECh. 1.5 - Prob. 49PPECh. 1.5 - Prob. 50PPECh. 1.5 - Prob. 51PPECh. 1.5 - Prob. 52PPECh. 1.5 - Prob. 53PPECh. 1.5 - Prob. 54PPECh. 1.5 - Prob. 55PPECh. 1.5 - Prob. 56PPECh. 1.5 - Prob. 57PPECh. 1.5 - Prob. 58PPECh. 1.5 - Prob. 59PPECh. 1.5 - Prob. 60PPECh. 1.5 - Prob. 61PPECh. 1.5 - Prob. 62PPECh. 1.5 - Prob. 63PPECh. 1.5 - Prob. 64PPECh. 1.5 - Prob. 65PPECh. 1.5 - Prob. 66PPECh. 1.5 - Prob. 67PPECh. 1.5 - Prob. 68PPECh. 1.5 - Prob. 69PPECh. 1.5 - Prob. 70STPCh. 1.5 - Prob. 71STPCh. 1.5 - Prob. 72STPCh. 1.5 - Prob. 73STPCh. 1.5 - Prob. 74STPCh. 1.5 - Prob. 75MRCh. 1.5 - Prob. 76MRCh. 1.5 - Prob. 77MRCh. 1.5 - Prob. 78MRCh. 1.5 - Prob. 79MRCh. 1.5 - Prob. 80MRCh. 1.5 - Prob. 81MRCh. 1.5 - Prob. 82MRCh. 1.5 - Prob. 83MRCh. 1.5 - Prob. 84MRCh. 1.5 - Prob. 85MRCh. 1.6 - Prob. 1PCh. 1.6 - Prob. 2PCh. 1.6 - Prob. 3PCh. 1.6 - Prob. 4PCh. 1.6 - Prob. 1LCCh. 1.6 - Prob. 2LCCh. 1.6 - Prob. 3LCCh. 1.6 - Prob. 4LCCh. 1.6 - Prob. 5LCCh. 1.6 - Prob. 6LCCh. 1.6 - Prob. 7LCCh. 1.6 - Prob. 8PPECh. 1.6 - Prob. 9PPECh. 1.6 - Prob. 10PPECh. 1.6 - Prob. 11PPECh. 1.6 - Prob. 12PPECh. 1.6 - Prob. 13PPECh. 1.6 - Prob. 14PPECh. 1.6 - Prob. 15PPECh. 1.6 - Prob. 16PPECh. 1.6 - Prob. 17PPECh. 1.6 - Prob. 18PPECh. 1.6 - Prob. 19PPECh. 1.6 - Prob. 20PPECh. 1.6 - Prob. 21PPECh. 1.6 - Prob. 22PPECh. 1.6 - Prob. 23PPECh. 1.6 - Prob. 24PPECh. 1.6 - Prob. 25PPECh. 1.6 - Prob. 26PPECh. 1.6 - Prob. 27PPECh. 1.6 - Prob. 28PPECh. 1.6 - Prob. 29PPECh. 1.6 - Prob. 30PPECh. 1.6 - Prob. 31PPECh. 1.6 - Prob. 32PPECh. 1.6 - Prob. 33PPECh. 1.6 - Prob. 34PPECh. 1.6 - Prob. 35PPECh. 1.6 - Prob. 36PPECh. 1.6 - Prob. 37PPECh. 1.6 - Prob. 38PPECh. 1.6 - Prob. 39PPECh. 1.6 - Prob. 40PPECh. 1.6 - Prob. 41PPECh. 1.6 - Prob. 42PPECh. 1.6 - Prob. 43PPECh. 1.6 - Prob. 44PPECh. 1.6 - Prob. 45PPECh. 1.6 - Prob. 46PPECh. 1.6 - Prob. 47PPECh. 1.6 - Prob. 48PPECh. 1.6 - Prob. 49PPECh. 1.6 - Prob. 50PPECh. 1.6 - Prob. 51PPECh. 1.6 - Prob. 52PPECh. 1.6 - Prob. 53PPECh. 1.6 - Prob. 54PPECh. 1.6 - Prob. 55PPECh. 1.6 - Prob. 56PPECh. 1.6 - Prob. 57PPECh. 1.6 - Prob. 58PPECh. 1.6 - Prob. 59PPECh. 1.6 - Prob. 60PPECh. 1.6 - Prob. 61PPECh. 1.6 - Prob. 62PPECh. 1.6 - Prob. 63PPECh. 1.6 - Prob. 64PPECh. 1.6 - Prob. 65PPECh. 1.6 - Prob. 66PPECh. 1.6 - Prob. 67PPECh. 1.6 - Prob. 68PPECh. 1.6 - Prob. 69PPECh. 1.6 - Prob. 70STPCh. 1.6 - Prob. 71STPCh. 1.6 - Prob. 72STPCh. 1.6 - Prob. 73MRCh. 1.6 - Prob. 74MRCh. 1.6 - Prob. 75MRCh. 1.6 - Prob. 76MRCh. 1.6 - Prob. 77MRCh. 1.6 - Prob. 78MRCh. 1.6 - Prob. 1CBCh. 1.6 - Prob. 2CBCh. 1.6 - Prob. 3CBCh. 1.6 - Prob. 4CBCh. 1.6 - Prob. 5CBCh. 1.6 - Prob. 6CBCh. 1.6 - Prob. 7CBCh. 1.6 - Prob. 8CBCh. 1.6 - Prob. 9CBCh. 1.6 - Prob. 10CBCh. 1.6 - Prob. 11CBCh. 1.6 - Prob. 12CBCh. 1.6 - Prob. 13CBCh. 1.6 - Prob. 14CBCh. 1.6 - Prob. 15CBCh. 1.6 - Prob. 16CBCh. 1.6 - Prob. 17CBCh. 1.6 - Prob. 18CBCh. 1.7 - Prob. 1PCh. 1.7 - Prob. 2PCh. 1.7 - Prob. 3PCh. 1.7 - Prob. 4PCh. 1.7 - Prob. 5PCh. 1.7 - Prob. 1LCCh. 1.7 - Prob. 2LCCh. 1.7 - Prob. 3LCCh. 1.7 - Prob. 4LCCh. 1.7 - Prob. 5LCCh. 1.7 - Prob. 6LCCh. 1.7 - Prob. 7LCCh. 1.7 - Prob. 8LCCh. 1.7 - Prob. 9PPECh. 1.7 - Prob. 10PPECh. 1.7 - Prob. 11PPECh. 1.7 - Prob. 12PPECh. 1.7 - Prob. 13PPECh. 1.7 - Prob. 14PPECh. 1.7 - Prob. 15PPECh. 1.7 - Prob. 16PPECh. 1.7 - Prob. 17PPECh. 1.7 - Prob. 18PPECh. 1.7 - Prob. 19PPECh. 1.7 - Prob. 20PPECh. 1.7 - Prob. 21PPECh. 1.7 - Prob. 22PPECh. 1.7 - Prob. 23PPECh. 1.7 - Prob. 24PPECh. 1.7 - Prob. 25PPECh. 1.7 - Prob. 26PPECh. 1.7 - Prob. 27PPECh. 1.7 - Prob. 28PPECh. 1.7 - Prob. 29PPECh. 1.7 - Prob. 30PPECh. 1.7 - Prob. 31PPECh. 1.7 - Prob. 32PPECh. 1.7 - Prob. 33PPECh. 1.7 - Prob. 34PPECh. 1.7 - Prob. 35PPECh. 1.7 - Prob. 36PPECh. 1.7 - Prob. 37PPECh. 1.7 - Prob. 38PPECh. 1.7 - Prob. 39PPECh. 1.7 - Prob. 40PPECh. 1.7 - Prob. 41PPECh. 1.7 - Prob. 42PPECh. 1.7 - Prob. 43PPECh. 1.7 - Prob. 44PPECh. 1.7 - Prob. 45PPECh. 1.7 - Prob. 46PPECh. 1.7 - Prob. 47PPECh. 1.7 - Prob. 48PPECh. 1.7 - Prob. 49PPECh. 1.7 - Prob. 50PPECh. 1.7 - Prob. 51PPECh. 1.7 - Prob. 52PPECh. 1.7 - Prob. 53PPECh. 1.7 - Prob. 54PPECh. 1.7 - Prob. 55PPECh. 1.7 - Prob. 56PPECh. 1.7 - Prob. 57PPECh. 1.7 - Prob. 58PPECh. 1.7 - Prob. 59PPECh. 1.7 - Prob. 60PPECh. 1.7 - Prob. 61PPECh. 1.7 - Prob. 62PPECh. 1.7 - Prob. 63PPECh. 1.7 - Prob. 64PPECh. 1.7 - Prob. 65PPECh. 1.7 - Prob. 66PPECh. 1.7 - Prob. 67PPECh. 1.7 - Prob. 68PPECh. 1.7 - Prob. 69PPECh. 1.7 - Prob. 70PPECh. 1.7 - Prob. 71PPECh. 1.7 - Prob. 72PPECh. 1.7 - Prob. 73PPECh. 1.7 - Prob. 74PPECh. 1.7 - Prob. 75PPECh. 1.7 - Prob. 76PPECh. 1.7 - Prob. 77PPECh. 1.7 - Prob. 78PPECh. 1.7 - Prob. 79PPECh. 1.7 - Prob. 80PPECh. 1.7 - Prob. 81PPECh. 1.7 - Prob. 82PPECh. 1.7 - Prob. 83PPECh. 1.7 - Prob. 84PPECh. 1.7 - Prob. 85PPECh. 1.7 - Prob. 86PPECh. 1.7 - Prob. 87PPECh. 1.7 - Prob. 88PPECh. 1.7 - Prob. 89PPECh. 1.7 - Prob. 90PPECh. 1.7 - Prob. 1MPCh. 1.8 - Prob. 1PCh. 1.8 - Prob. 2PCh. 1.8 - Prob. 3PCh. 1.8 - Prob. 4PCh. 1.8 - Prob. 5PCh. 1.8 - Prob. 6PCh. 1.8 - Prob. 1LCCh. 1.8 - Prob. 2LCCh. 1.8 - Prob. 3LCCh. 1.8 - Prob. 4LCCh. 1.8 - Prob. 5LCCh. 1.8 - Prob. 6LCCh. 1.8 - Prob. 7PPECh. 1.8 - Prob. 8PPECh. 1.8 - Prob. 9PPECh. 1.8 - Prob. 10PPECh. 1.8 - Prob. 11PPECh. 1.8 - Prob. 12PPECh. 1.8 - Prob. 13PPECh. 1.8 - Prob. 14PPECh. 1.8 - Prob. 15PPECh. 1.8 - Prob. 16PPECh. 1.8 - Prob. 17PPECh. 1.8 - Prob. 18PPECh. 1.8 - Prob. 19PPECh. 1.8 - Prob. 20PPECh. 1.8 - Prob. 21PPECh. 1.8 - Prob. 22PPECh. 1.8 - Prob. 23PPECh. 1.8 - Prob. 24PPECh. 1.8 - Prob. 25PPECh. 1.8 - Prob. 26PPECh. 1.8 - Prob. 27PPECh. 1.8 - Prob. 28PPECh. 1.8 - Prob. 29PPECh. 1.8 - Prob. 30PPECh. 1.8 - Prob. 31PPECh. 1.8 - Prob. 32PPECh. 1.8 - Prob. 33PPECh. 1.8 - Prob. 34PPECh. 1.8 - Prob. 35PPECh. 1.8 - Prob. 36PPECh. 1.8 - Prob. 37PPECh. 1.8 - Prob. 38PPECh. 1.8 - Prob. 39PPECh. 1.8 - Prob. 40PPECh. 1.8 - Prob. 41PPECh. 1.8 - Prob. 42PPECh. 1.8 - Prob. 43PPECh. 1.8 - Prob. 44PPECh. 1.8 - Prob. 45PPECh. 1.8 - Prob. 46PPECh. 1.8 - Prob. 47PPECh. 1.8 - Prob. 48PPECh. 1.8 - Prob. 49PPECh. 1.8 - Prob. 50PPECh. 1.8 - Prob. 51PPECh. 1.8 - Prob. 52PPECh. 1.8 - Prob. 53PPECh. 1.8 - Prob. 54PPECh. 1.8 - Prob. 55PPECh. 1.8 - Prob. 56PPECh. 1.8 - Prob. 57PPECh. 1.8 - Prob. 58PPECh. 1.8 - Prob. 59PPECh. 1.8 - Prob. 60PPECh. 1.8 - Prob. 61PPECh. 1.8 - Prob. 62PPECh. 1.8 - Prob. 63PPECh. 1.8 - Prob. 64PPECh. 1.8 - Prob. 65PPECh. 1.8 - Prob. 66PPECh. 1.8 - Prob. 1MPCh. 1.8 - Prob. 1CBCh. 1.8 - Prob. 2CBCh. 1.9 - Prob. 1RCh. 1.9 - Prob. 2RCh. 1.9 - Prob. 3RCh. 1.9 - Prob. 4RCh. 1.9 - Prob. 1PCh. 1.9 - Prob. 2PCh. 1.9 - Prob. 3PCh. 1.9 - Prob. 1LCCh. 1.9 - Prob. 2LCCh. 1.9 - Prob. 3LCCh. 1.9 - Prob. 4LCCh. 1.9 - Prob. 5LCCh. 1.9 - Prob. 6LCCh. 1.9 - Prob. 7LCCh. 1.9 - Prob. 8PPECh. 1.9 - Prob. 9PPECh. 1.9 - Prob. 10PPECh. 1.9 - Prob. 11PPECh. 1.9 - Prob. 12PPECh. 1.9 - Prob. 13PPECh. 1.9 - Prob. 14PPECh. 1.9 - Prob. 15PPECh. 1.9 - Prob. 16PPECh. 1.9 - Prob. 17PPECh. 1.9 - Prob. 18PPECh. 1.9 - Prob. 19PPECh. 1.9 - Prob. 20PPECh. 1.9 - Prob. 21PPECh. 1.9 - Prob. 22PPECh. 1.9 - Prob. 23PPECh. 1.9 - Prob. 24PPECh. 1.9 - Prob. 25PPECh. 1.9 - Prob. 26PPECh. 1.9 - Prob. 27PPECh. 1.9 - Prob. 28PPECh. 1.9 - Prob. 29PPECh. 1.9 - Prob. 30PPECh. 1.9 - Prob. 31PPECh. 1.9 - Prob. 32PPECh. 1.9 - Prob. 33PPECh. 1.9 - Prob. 34PPECh. 1.9 - Prob. 35PPECh. 1.9 - Prob. 36STPCh. 1.9 - Prob. 37STPCh. 1.9 - Prob. 38STPCh. 1.9 - Prob. 39STPCh. 1.9 - Prob. 40MRCh. 1.9 - Prob. 41MRCh. 1.9 - Prob. 42MRCh. 1.9 - Prob. 43MRCh. 1.9 - Prob. 44MRCh. 1.9 - Prob. 45MRCh. 1.9 - Prob. 46MRCh. 1.9 - Prob. 47MRCh. 1.9 - Prob. 48MRCh. 1.9 - Prob. 49MRCh. 1.9 - Prob. 50MRCh. 1.9 - Prob. 51MRCh. 1.9 - Prob. 52MRCh. 1.9 - Prob. 53MRCh. 1.9 - Prob. 54MRCh. 1 - Prob. 1GRCh. 1 - Prob. 2GRCh. 1 - Prob. 3GRCh. 1 - Prob. 4GRCh. 1 - Prob. 5GRCh. 1 - Prob. 6GRCh. 1 - Prob. 7GRCh. 1 - Prob. 8GRCh. 1 - Prob. 9GRCh. 1 - Prob. 10GRCh. 1 - Prob. 11GRCh. 1 - Prob. 12GRCh. 1 - Prob. 13GRCh. 1 - Prob. 14GRCh. 1 - Prob. 15GRCh. 1 - Prob. 16GRCh. 1 - Prob. 17GRCh. 1 - Prob. 18GRCh. 1 - Prob. 19GRCh. 1 - Prob. 20GRCh. 1 - Prob. 21GRCh. 1 - Prob. 22GRCh. 1 - Prob. 23GRCh. 1 - Prob. 24GRCh. 1 - Prob. 25GRCh. 1 - Prob. 26GRCh. 1 - Prob. 27GRCh. 1 - Prob. 1CRCh. 1 - Prob. 2CRCh. 1 - Prob. 3CRCh. 1 - Prob. 4CRCh. 1 - Prob. 5CRCh. 1 - Prob. 6CRCh. 1 - Prob. 7CRCh. 1 - Prob. 8CRCh. 1 - Prob. 9CRCh. 1 - Prob. 10CRCh. 1 - Prob. 11CRCh. 1 - Prob. 12CRCh. 1 - Prob. 13CRCh. 1 - Prob. 14CRCh. 1 - Prob. 15CRCh. 1 - Prob. 16CRCh. 1 - Prob. 17CRCh. 1 - Prob. 18CRCh. 1 - Prob. 19CRCh. 1 - Prob. 20CRCh. 1 - Prob. 21CRCh. 1 - Prob. 22CRCh. 1 - Prob. 23CRCh. 1 - Prob. 24CRCh. 1 - Prob. 25CRCh. 1 - Prob. 26CRCh. 1 - Prob. 27CRCh. 1 - Prob. 28CRCh. 1 - Prob. 29CRCh. 1 - Prob. 30CRCh. 1 - Prob. 31CRCh. 1 - Prob. 32CRCh. 1 - Prob. 33CRCh. 1 - Prob. 34CRCh. 1 - Prob. 35CRCh. 1 - Prob. 36CRCh. 1 - Prob. 37CRCh. 1 - Prob. 38CRCh. 1 - Prob. 39CRCh. 1 - Prob. 40CRCh. 1 - Prob. 41CRCh. 1 - Prob. 42CRCh. 1 - Prob. 43CRCh. 1 - Prob. 44CRCh. 1 - Prob. 45CRCh. 1 - Prob. 46CRCh. 1 - Prob. 47CRCh. 1 - Prob. 48CRCh. 1 - Prob. 49CRCh. 1 - Prob. 50CRCh. 1 - Prob. 51CRCh. 1 - Prob. 52CRCh. 1 - Prob. 53CRCh. 1 - Prob. 54CRCh. 1 - Prob. 55CRCh. 1 - Prob. 56CRCh. 1 - Prob. 57CRCh. 1 - Prob. 58CRCh. 1 - Prob. 59CRCh. 1 - Prob. 60CRCh. 1 - Prob. 61CRCh. 1 - Prob. 62CRCh. 1 - Prob. 63CRCh. 1 - Prob. 64CRCh. 1 - Prob. 65CRCh. 1 - Prob. 66CRCh. 1 - Prob. 67CRCh. 1 - Prob. 68CRCh. 1 - Prob. 69CRCh. 1 - Prob. 70CRCh. 1 - Prob. 71CRCh. 1 - Prob. 72CRCh. 1 - Prob. 73CRCh. 1 - Prob. 74CRCh. 1 - Prob. 75CRCh. 1 - Prob. 76CRCh. 1 - Prob. 77CRCh. 1 - Prob. 78CRCh. 1 - Prob. 79CRCh. 1 - Prob. 80CRCh. 1 - Prob. 81CRCh. 1 - Prob. 82CRCh. 1 - Prob. 83CRCh. 1 - Prob. 84CRCh. 1 - Prob. 85CRCh. 1 - Prob. 86CRCh. 1 - Prob. 87CRCh. 1 - Prob. 88CRCh. 1 - Prob. 89CRCh. 1 - Prob. 90CRCh. 1 - Prob. 91CRCh. 1 - Prob. 92CRCh. 1 - Prob. 93CRCh. 1 - Prob. 94CRCh. 1 - Prob. 95CRCh. 1 - Prob. 96CRCh. 1 - Prob. 97CRCh. 1 - Prob. 98CRCh. 1 - Prob. 99CRCh. 1 - Prob. 1CTCh. 1 - Prob. 2CTCh. 1 - Prob. 3CTCh. 1 - Prob. 4CTCh. 1 - Prob. 5CTCh. 1 - Prob. 6CTCh. 1 - Prob. 7CTCh. 1 - Prob. 8CTCh. 1 - Prob. 9CTCh. 1 - Prob. 10CTCh. 1 - Prob. 11CTCh. 1 - Prob. 12CTCh. 1 - Prob. 13CTCh. 1 - Prob. 14CTCh. 1 - Prob. 15CTCh. 1 - Prob. 16CTCh. 1 - Prob. 17CTCh. 1 - Prob. 18CTCh. 1 - Prob. 19CTCh. 1 - Prob. 20CTCh. 1 - Prob. 21CTCh. 1 - Prob. 22CTCh. 1 - Prob. 23CTCh. 1 - Prob. 24CTCh. 1 - Prob. 1CCSRCh. 1 - Prob. 2CCSRCh. 1 - Prob. 3CCSRCh. 1 - Prob. 4CCSRCh. 1 - Prob. 5CCSRCh. 1 - Prob. 6CCSRCh. 1 - Prob. 7CCSRCh. 1 - Prob. 8CCSRCh. 1 - Prob. 9CCSRCh. 1 - Prob. 10CCSRCh. 1 - Prob. 11CCSRCh. 1 - Prob. 12CCSRCh. 1 - Prob. 13CCSRCh. 1 - Prob. 14CCSRCh. 1 - Prob. 15CCSRCh. 1 - Prob. 16CCSRCh. 1 - Prob. 17CCSRCh. 1 - Prob. 18CCSRCh. 1 - Prob. 19CCSRCh. 1 - Prob. 20CCSRCh. 1 - Prob. 21CCSRCh. 1 - Prob. 22CCSRCh. 1 - Prob. 23CCSRCh. 1 - Prob. 24CCSR

Additional Math Textbook Solutions

Find more solutions based on key concepts
In the following exercises, divide. Then check by multiplying. 864

PREALGEBRA

In each of Exercises 21–30, draw a linear graph to represent the given information. Be sure to label and number...

Elementary Algebra: Concepts and Applications (10th Edition)

1. combination of numbers, variables, and operation symbols is called an algebraic______.

Algebra and Trigonometry (6th Edition)

Problems Prove that f(gh)=(fg)h.

Differential Equations and Linear Algebra (4th Edition)

Solve each formula for the given letter . [2.3] What percent of 60 is 42? [2.4]

Elementary and Intermediate Algebra: Concepts and Applications (7th Edition)

Practice Exercises In Exercises 1—20, find all numbers for which each rational expression is undefined. If th...

Introductory and Intermediate Algebra for College Students (5th Edition)

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Text book image
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
Text book image
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
Introduction to Integers,Maths - What are integers - English; Author: Mathispower4u;https://www.youtube.com/watch?v=04pURxo-iu0;License: Standard YouTube License, CC-BY
Integers-Middle School Math; Author: MooMooMath and Science;https://www.youtube.com/watch?v=DGWcWtqM_yk;License: Standard YouTube License, CC-BY