Chapter 17, Problem 17.13QAP

Interpretation Introduction

(a)

Interpretation:

For an angle of incidence of 45⁰, the effective penetration depth of the evanescent wave should be determined. Penetration depth if the angle changed to 60⁰ should be determined.

Concept introduction:

The effective penetration depth can be calculated as follows:

$d_p=\frac{{\lambda }_c}{2\pi {\left[{\sin }^2\theta -{\left(n_s/n_c\right)}^2\right]}^{1/2}}$

Here,

$\begin{array}{l}{d}_p-\text{ effective penetration depth}\\ {\lambda }_c-\text{ Wavelength of the beam}\\ \theta -\text{ incident angle}\\ n_s-\text{ refractive index of the sample}\\ n_c-\text{refractive index of the crystal}\end{array}$

Answer to Problem 17.13QAP

When the angle of incidence = 45⁰

$d_p=1.64\times {10}^{-6}\text{ m}$

When the angle of incidence = 60⁰

$d_p=1.14\times {10}^{-6}\text{ m}$

Explanation of Solution

When the angle of incidence = 45⁰

$\begin{array}{l}{d}_p=\frac{\left(1/2000\right)\times {10}^{-2}}{2\times 3.14{\left[{\sin }^{2}45-{\left(1.03/2.00\right)}^2\right]}^{1/2}}\\ d_p=\frac{5\times {10}^{-6}}{2\times 3.14{\left[0.5-0.265\right]}^{1/2}}\\ d_p=1.64\times {10}^{-6}\text{ m}\end{array}$

When the angle of incidence = 60⁰

$\begin{array}{l}{d}_p=\frac{\left(1/2000\right)\times {10}^{-2}}{2\times 3.14{\left[{\sin }^{2}60-{\left(1.03/2.00\right)}^2\right]}^{1/2}}\\ d_p=\frac{5\times {10}^{-6}}{2\times 3.14{\left[0.75-0.265\right]}^{1/2}}\\ d_p=1.14\times {10}^{-6}\text{ m}\end{array}$

Interpretation Introduction

(b)

Interpretation:

The penetration depths for sample refractive indexes varying from 1.00 to 1.70 in steps of 0.10 should be determined. Penetration depth should be plotted as a function of refractive index. The refractive index for which the penetration depth becomes zero should be determined.

Concept introduction:

$\begin{array}{l}{d}_p=\frac{{\lambda }_c}{2\pi {\left[{\sin }^2\theta -{\left(n_s/n_c\right)}^2\right]}^{1/2}}\\ d_p-\text{ effective penetration depth}\\ {\lambda }_c-\text{ Wavelength of the beam}\\ \theta -\text{ incident angle}\\ n_s-\text{ refractive index of the sample}\\ n_c-\text{refractive index of the crystal}\end{array}$

Answer to Problem 17.13QAP

The plot is represented as follows:

Explanation of Solution

The data given is as follows:

Refractive index of sample	dp, m
1.00	1.12597E-06
1.10	1.19018E-06
1.20	1.27491E-06
1.30	1.39125E-06
1.40	1.56143E-06
1.50	1.8387E-06
1.60	2.40057E-06
1.70	4.80114E-06

The plot for the data is represented as follows:

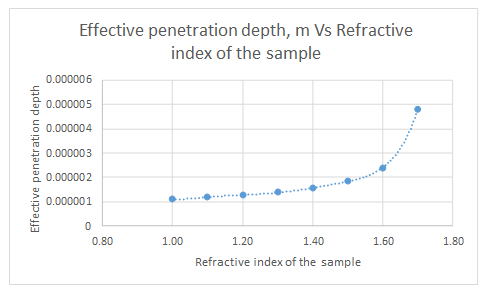
From the graph, it can be seen that the refractive index never approaches zero.

Interpretation Introduction

(c)

Interpretation:

For a sample with a refractive index 1.37 at 2000 cm-1 and incident angle of 45⁰, the penetration depth versus the ATR crystal refractive index should be plotted.

Concept introduction:

The effective penetration depth can be calculated as follows:

$d_p=\frac{{\lambda }_c}{2\pi {\left[{\sin }^2\theta -{\left(n_s/n_c\right)}^2\right]}^{1/2}}$

Here,

$\begin{array}{l}{d}_p-\text{ effective penetration depth}\\ {\lambda }_c-\text{ Wavelength of the beam}\\ \theta -\text{ incident angle}\\ n_s-\text{ refractive index of the sample}\\ n_c-\text{refractive index of the crystal}\end{array}$

Answer to Problem 17.13QAP

Ge crystal will give smaller penetration depth as a refractive index of the crystal increases, the effective penetration depth decreases.

Explanation of Solution

The data given is as follows:

Refractive index of Crystal	dp, m
2.00	4.53849E-06
2.25	2.21456E-06
2.50	1.78166E-06
2.75	1.58661E-06
3.00	1.47477E-06
3.25	1.40242E-06
3.50	1.35201E-06
3.75	1.31509E-06
4.00	1.28702E-06

The plot is represented as follows:

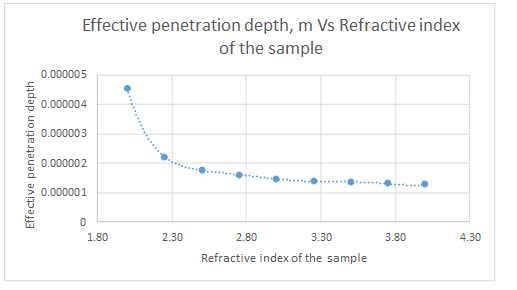
Ge crystal will give smaller penetration depth as a refractive index of the crystal increases, the effective penetration depth decreases.

Interpretation Introduction

(d)

Interpretation:

The effective penetration depth at 3000 cm-1, 2000 cm-1 and 2000 cm-1 should be determined.

Concept introduction:

The effective penetration depth can be calculated as follows:

$d_p=\frac{{\lambda }_c}{2\pi {\left[{\sin }^2\theta -{\left(n_s/n_c\right)}^2\right]}^{1/2}}$

Here,

$\begin{array}{l}{d}_p-\text{ effective penetration depth}\\ {\lambda }_c-\text{ Wavelength of the beam}\\ \theta -\text{ incident angle}\\ n_s-\text{ refractive index of the sample}\\ n_c-\text{refractive index of the crystal}\end{array}$

Answer to Problem 17.13QAP

At 3000 cm-1

$d_p=8.69\times {10}^{-7}\text{m}$

At 2000 cm-1

$d_p=1.31\times {10}^{-6}\text{m}$

At 1000 cm-1

$d_p=2.61\times {10}^{-6}\text{m}$

Explanation of Solution

At 3000 cm-1

$\begin{array}{l}{d}_p=\frac{\left(1/3000\right)\times {10}^{-2}\text{ m}}{2\times 3.14{\left[{\sin }^{2}45-{\left(1.003/2.8\right)}^2\right]}^{1/2}}\\ d_p=\frac{3.33\times {10}^{-6}}{3.83}\\ d_p=8.69\times {10}^{-7}\text{m}\end{array}$

At 2000 cm-1

$\begin{array}{l}{d}_p=\frac{\left(1/2000\right)\times {10}^{-2}\text{ m}}{2\times 3.14{\left[{\sin }^{2}45-{\left(1.003/2.8\right)}^2\right]}^{1/2}}\\ d_p=\frac{5\times {10}^{-6}}{3.83}\\ d_p=1.31\times {10}^{-6}\text{m}\end{array}$

At 1000 cm-1

$\begin{array}{l}{d}_p=\frac{\left(1/1000\right)\times {10}^{-2}\text{ m}}{2\times 3.14{\left[{\sin }^{2}45-{\left(1.003/2.8\right)}^2\right]}^{1/2}}\\ d_p=\frac{1\times {10}^{-5}}{3.83}\\ d_p=2.61\times {10}^{-6}\text{m}\end{array}$

In case of analyzing aqueous samples, pouring shallow amount over the surface of the crystal is sufficient. Since trace amounts are used to analyze, absorption by the aqueous solvent is not a problem.

Interpretation Introduction

(e)

Interpretation:

The principles of the new method to obtain a depth profile of a sample surface using ATR spectroscopy should be described.

Concept introduction:

In ATR spectroscopy through the ATR crystal, an infrared beam is passed such that it reflects off the internal surface at least once when in contact with the sample. This reflection results in an evanescent wave which goes into the sample. The penetration depth is determined by the wavelength of IR beam, angle of incidence, refractive indexes of sample and the crystal.

Explanation of Solution

A new depth profiling method using multiple-angle ATR/FT-IR spectroscopy has been developed.

First, a profile frequency is defined then the stratified medium is defined. Matrix A is generated from interpolated absorptances and matrix E is generated from estimated mean square electric fields. Linear equations of absorptance by SVD method is solved and the first estimated refractive index profile from matrix X is calculated. Nonlinear fittings of the reflectances are determined by Levenberg-Marquadt method. Finally, complex refractive index profile is obtained.