
Concept explainers
PRINTED BY: 92248ddb24ccbc6@placeholder.10274.edu. Printing is for personal, private use only. No part of this book may be reproduced or transmitted without publisher's prior permission. Violators will be prosecuted.
A construction project has indirect costs totaling $40,000 per week. Major activities in the project and their expected times in weeks are shown in this precedence diagram.
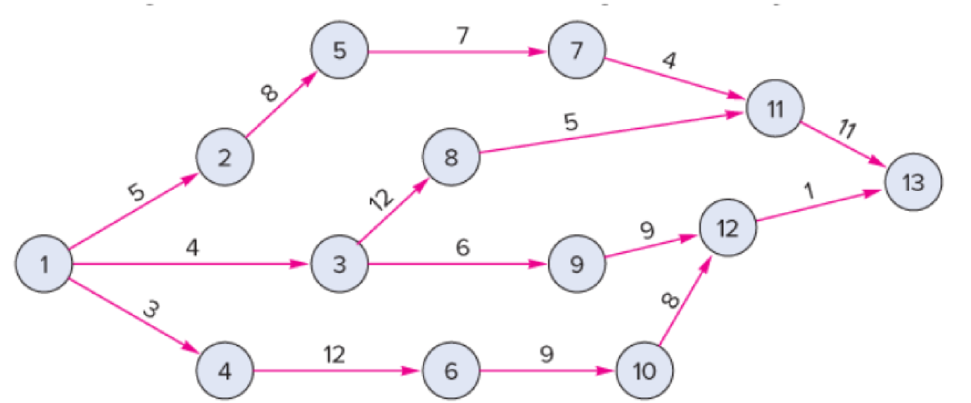
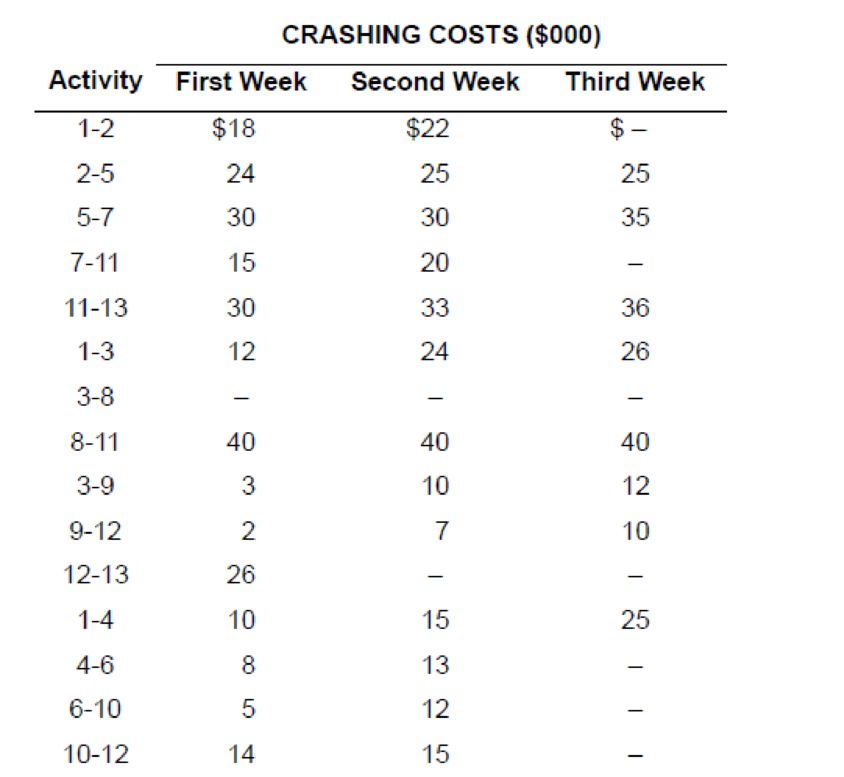
Crashing costs for each activity are:
a. Determine the optimum time–cost crashing plan.
b. Plot the total-cost curve that describes the least expensive crashing
a)
To determine: The optimum cost-saving plan.
Introduction:
Project crashing:
It is method to shorten the total time taken for a project by reducing the time taken for one or more activities on the critical path. The reduction in the normal time taken is known as crashing.
Answer to Problem 15P
Explanation of Solution
Given information:
- Indirect cost is $40,000 per week.
| Activity | Crash cost first week ($000) | Crash cost second week ($000) | Crash cost third week ($000) |
| 1 to 2 | 18 | 22 | |
| 2 to 5 | 24 | 25 | 25 |
| 5 to 7 | 30 | 30 | 35 |
| 7 to 11 | 15 | 20 | |
| 11 to 13 | 30 | 33 | 36 |
| 1 to 3 | 12 | 24 | 26 |
| 3 to 8 | |||
| 8 to 11 | 40 | 40 | 40 |
| 3 to 9 | 3 | 10 | 12 |
| 9 to 12 | 2 | 7 | 10 |
| 12 to 13 | 26 | ||
| 1 to 4 | 10 | 15 | 25 |
| 4 to 6 | 8 | 13 | |
| 6 to 10 | 5 | 12 | |
| 10 to 12 | 14 | 15 |
Project crashing:
Calculation of expected duration of each path:
Path 1-2-5-7-11-13:
Path 1-3-8-11-13:
Path 1-3-9-12-13:
Path 1-4-6-10-12-13:
Step 1:
Critical path is 1-2-5-7-11-13.
The activities are ranked according to the cost per week to crash.
| Activity | Cost ($) |
| 7-11 | 15 |
| 1-2 | 18 |
| 2-5 | 24 |
| 5-7 | 30 |
| 11-13 | 30 |
Activity 7-11 will be crashed first by 1 week since it has the lowest crashing cost ($15) and this cost is ≤ 40. Path 1-2-5-7-11-13 will decrease by 1 week.
Step 2:
The paths and new expected duration are:
| Path | Expected Duration |
| 1-2-5-7-11-13 | 34 |
| 1-3-8-11-13 | 32 |
| 1-3-9-12-13 | 20 |
| 1-4-6-10-12-13 | 33 |
Critical path is 1-2-5-7-11-13.
The activities are ranked according to the cost per week to crash.
| Activity | Cost ($) |
| 1-2 | $18 |
| 7-11 | $20 |
| 2-5 | $24 |
| 5-7 | $30 |
| 11-13 | $30 |
Activity 1-2 will be crashed first by 1 week since it has the lowest crashing cost ($18) and this cost is ≤ 40. Path 1-2-5-7-11-13 will decrease by 1 week.
Step 3:
The paths and new expected duration are:
| Path | Expected Duration |
| 1-2-5-7-11-13 | 33 |
| 1-3-8-11-13 | 32 |
| 1-3-9-12-13 | 20 |
| 1-4-6-10-12-13 | 33 |
Critical path is 1-2-5-7-11-13 and 1-4-6-10-12-13.
The activities are ranked according to the cost per week to crash.
| Path | Activity | Cost ($) |
| 1-2-5-7-11-13 | 7-11 | $20 |
| 1-2 | $22 | |
| 2-5 | $24 | |
| 5-7 | $30 | |
| 11-13 | $30 | |
| 1-4-6-10-12-13 | 6-10 | $5 |
| 4-6 | $8 | |
| 1-4 | $10 | |
| 10-12 | $14 | |
| 12-13 | $26 |
Activity 7-11 will be crashed first by 1 week since it has the lowest crashing cost ($20). Path 1-2-5-7-11-13 will decrease by 1 week.
Activity 6-10 will be crashed first by 1 week since it has the lowest crashing cost ($5). Path 1-4-6-10-12-13 will decrease by 1 week.
The combined crash cost ($25) is ≤ $40.
Step 4:
The paths and new expected duration are:
| Path | Expected Duration |
| 1-2-5-7-11-13 | 32 |
| 1-3-8-11-13 | 32 |
| 1-3-9-12-13 | 20 |
| 1-4-6-10-12-13 | 32 |
Critical path is 1-2-5-7-11-13, 1-3-8-11-13, and 1-4-6-10-12-13.
The activities are ranked according to the cost per week to crash.
| Path | Activity | Cost ($) |
| 1-2-5-7-11-13 | 1-2 | $22 |
| 2-5 | $24 | |
| 5-7 | $30 | |
| 11-13 | $30 | |
| 1-3-8-11-13 | 1-3 | $12 |
| 11-13 | $30 | |
| 8-11 | $40 | |
| 1-4-6-10-12-13 | 4-6 | $8 |
| 1-4 | $10 | |
| 6-10 | $12 | |
| 10-12 | $14 | |
| 12-13 | $26 |
Activity 11-13 will be crashed first by 1 week since it has the lowest crashing cost ($30). Paths 1-2-5-7-11-13 and 1-3-8-11-13 will decrease by 1 week.
Activity 4-6 will be crashed first by 1 week since it has the lowest crashing cost ($8). Path 1-4-6-10-12-13 will decrease by 1 week.
The combined crash cost ($38) is ≤ $40.
Step 5:
The paths and new expected duration are:
| Path | Expected Duration |
| 1-2-5-7-11-13 | 31 |
| 1-3-8-11-13 | 31 |
| 1-3-9-12-13 | 20 |
| 1-4-6-10-12-13 | 31 |
Critical path is 1-2-5-7-11-13, 1-3-8-11-13, and 1-4-6-10-12-13.
The activities are ranked according to the cost per week to crash.
| Path | Activity | Cost ($) |
| 1-2-5-7-11-13 | 1-2 | $22 |
| 2-5 | $24 | |
| 5-7 | $30 | |
| 11-13 | $33 | |
| 1-3-8-11-13 | 1-3 | $12 |
| 11-13 | $33 | |
| 8-11 | $40 | |
| 1-4-6-10-12-13 | 1-4 | $10 |
| 6-10 | $12 | |
| 4-6 | $13 | |
| 10-12 | $14 | |
| 12-13 | $26 |
Activity 11-13 could be crashed first by 1 week since it has the lowest crashing cost ($33). Paths 1-2-5-7-11-13 and 1-3-8-11-13 will decrease by 1 week.
Activity 1-4 could be crashed first by 1 week since it has the lowest crashing cost ($10). Path 1-4-6-10-12-13 will decrease by 1 week.
The combined crash cost ($43) is ≥ $40.
Since the marginal cost of crashing is greater than the marginal benefit of crashing, crashing will be stopped at step 4.
The final project duration time is 31 weeks. The activities that are crashed are:
Activity 7-11 (First week)
Activity 7-11 (Second week)
Activity 1-2
Activity 6-10
Activity 11-13
Activity 4-6
Calculation of total crashing cost:
The total crashing cost is calculated by summing the crashing cost involved all the steps and the indirect costs every week.
The activities to be crashed are: 7-11, 1-2, 6-10, 11-13, and 4-6. The total crashing cost is $1,336,000.
b)
To Plot: The cost curve with the least expensive crashing which will reduce the project by 6 weeks.
Introduction:
Project crashing:
It is method to shorten the total time taken for a project by reducing the time taken for one or more activities on the critical path. The reduction in the normal time taken is known as crashing.
Answer to Problem 15P
Cost curve:
Explanation of Solution
Given information:
- Indirect cost is $40,000 per week.
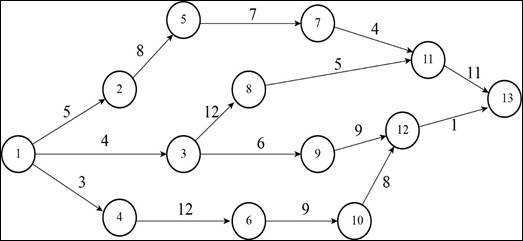
| Activity | Crash cost first week ($000) | Crash cost second week ($000) | Crash cost third week ($000) |
| 1 to 2 | 18 | 22 | |
| 2 to 5 | 24 | 25 | 25 |
| 5 to 7 | 30 | 30 | 35 |
| 7 to 11 | 15 | 20 | |
| 11 to 13 | 30 | 33 | 36 |
| 1 to 3 | 12 | 24 | 26 |
| 3 to 8 | |||
| 8 to 11 | 40 | 40 | 40 |
| 3 to 9 | 3 | 10 | 12 |
| 9 to 12 | 2 | 7 | 10 |
| 12 to 13 | 26 | ||
| 1 to 4 | 10 | 15 | 25 |
| 4 to 6 | 8 | 13 | |
| 6 to 10 | 5 | 12 | |
| 10 to 12 | 14 | 15 |
Project crashing:
Calculation of expected duration of each path:
Path 1-2-5-7-11-13:
Path 1-3-8-11-13:
Path 1-3-9-12-13:
Path 1-4-6-10-12-13:
Step 1:
Critical path is 1-2-5-7-11-13.
The activities are ranked according to the cost per week to crash.
| Activity | Cost ($) |
| 7-11 | 15 |
| 1-2 | 18 |
| 2-5 | 24 |
| 5-7 | 30 |
| 11-13 | 30 |
Activity 7-11 will be crashed first by 1 week since it has the lowest crashing cost ($15) and this cost is ≤ 40. Path 1-2-5-7-11-13 will decrease by 1 week.
Step 2:
The paths and new expected duration are:
| Path | Expected Duration |
| 1-2-5-7-11-13 | 34 |
| 1-3-8-11-13 | 32 |
| 1-3-9-12-13 | 20 |
| 1-4-6-10-12-13 | 33 |
Critical path is 1-2-5-7-11-13.
The activities are ranked according to the cost per week to crash.
| Activity | Cost ($) |
| 1-2 | $18 |
| 7-11 | $20 |
| 2-5 | $24 |
| 5-7 | $30 |
| 11-13 | $30 |
Activity 1-2 will be crashed first by 1 week since it has the lowest crashing cost ($18) and this cost is ≤ 40. Path 1-2-5-7-11-13 will decrease by 1 week.
Step 3:
The paths and new expected duration are:
| Path | Expected Duration |
| 1-2-5-7-11-13 | 33 |
| 1-3-8-11-13 | 32 |
| 1-3-9-12-13 | 20 |
| 1-4-6-10-12-13 | 33 |
Critical path is 1-2-5-7-11-13 and 1-4-6-10-12-13.
The activities are ranked according to the cost per week to crash.
| Path | Activity | Cost ($) |
| 1-2-5-7-11-13 | 7-11 | $20 |
| 1-2 | $22 | |
| 2-5 | $24 | |
| 5-7 | $30 | |
| 11-13 | $30 | |
| 1-4-6-10-12-13 | 6-10 | $5 |
| 4-6 | $8 | |
| 1-4 | $10 | |
| 10-12 | $14 | |
| 12-13 | $26 |
Activity 7-11 will be crashed first by 1 week since it has the lowest crashing cost ($20). Path 1-2-5-7-11-13 will decrease by 1 week.
Activity 6-10 will be crashed first by 1 week since it has the lowest crashing cost ($5). Path 1-4-6-10-12-13 will decrease by 1 week.
The combined crash cost ($25) is ≤ $40.
Step 4:
The paths and new expected duration are:
| Path | Expected Duration |
| 1-2-5-7-11-13 | 32 |
| 1-3-8-11-13 | 32 |
| 1-3-9-12-13 | 20 |
| 1-4-6-10-12-13 | 32 |
Critical path is 1-2-5-7-11-13, 1-3-8-11-13, and 1-4-6-10-12-13.
The activities are ranked according to the cost per week to crash.
| Path | Activity | Cost ($) |
| 1-2-5-7-11-13 | 1-2 | $22 |
| 2-5 | $24 | |
| 5-7 | $30 | |
| 11-13 | $30 | |
| 1-3-8-11-13 | 1-3 | $12 |
| 11-13 | $30 | |
| 8-11 | $40 | |
| 1-4-6-10-12-13 | 4-6 | $8 |
| 1-4 | $10 | |
| 6-10 | $12 | |
| 10-12 | $14 | |
| 12-13 | $26 |
Activity 11-13 will be crashed first by 1 week since it has the lowest crashing cost ($30). Paths 1-2-5-7-11-13 and 1-3-8-11-13 will decrease by 1 week.
Activity 4-6 will be crashed first by 1 week since it has the lowest crashing cost ($8). Path 1-4-6-10-12-13 will decrease by 1 week.
The combined crash cost ($38) is ≤ $40.
Step 5:
The paths and new expected duration are:
| Path | Expected Duration |
| 1-2-5-7-11-13 | 31 |
| 1-3-8-11-13 | 31 |
| 1-3-9-12-13 | 20 |
| 1-4-6-10-12-13 | 31 |
Critical path is 1-2-5-7-11-13, 1-3-8-11-13, and 1-4-6-10-12-13.
The activities are ranked according to the cost per week to crash.
| Path | Activity | Cost ($) |
| 1-2-5-7-11-13 | 1-2 | $22 |
| 2-5 | $24 | |
| 5-7 | $30 | |
| 11-13 | $33 | |
| 1-3-8-11-13 | 1-3 | $12 |
| 11-13 | $33 | |
| 8-11 | $40 | |
| 1-4-6-10-12-13 | 1-4 | $10 |
| 6-10 | $12 | |
| 4-6 | $13 | |
| 10-12 | $14 | |
| 12-13 | $26 |
Activity 11-13 will be crashed first by 1 week since it has the lowest crashing cost ($33). Paths 1-2-5-7-11-13 and 1-3-8-11-13 will decrease by 1 week.
Activity 1-4 will be crashed first by 1 week since it has the lowest crashing cost ($10). Path 1-4-6-10-12-13 will decrease by 1 week. The combined crash cost is ($43).
Step 6:
The paths and new expected duration are:
| Path | Expected Duration |
| 1-2-5-7-11-13 | 30 |
| 1-3-8-11-13 | 30 |
| 1-3-9-12-13 | 20 |
| 1-4-6-10-12-13 | 30 |
Critical path is 1-2-5-7-11-13, 1-3-8-11-13, and 1-4-6-10-12-13.
The activities are ranked according to the cost per week to crash.
| Path | Activity | Cost ($) |
| 1-2-5-7-11-13 | 1-2 | $22 |
| 2-5 | $24 | |
| 5-7 | $30 | |
| 11-13 | $36 | |
| 1-3-8-11-13 | 1-3 | $12 |
| 11-13 | $36 | |
| 8-11 | $40 | |
| 1-4-6-10-12-13 | 6-10 | $12 |
| 4-6 | $13 | |
| 10-12 | $14 | |
| 1-4 | $15 | |
| 12-13 | $26 |
Activity 1-2 will be crashed first by 1 week since it has the lowest crashing cost ($22). Path 1-2-5-7-11-13 will decrease by 1 week.
Activity 1-3 will be crashed first by 1 week since it has the lowest crashing cost ($12). Path 1-3-8-11-13 will decrease by 1 week.
Activity 6-10 will be crashed first by 1 week since it has the lowest crashing cost ($12). Path 1-4-6-10-12-13 will decrease by 1 week. The combined crash cost is ($436.
The final project duration time is 29 weeks. The activities that are crashed are:
Activity 7-11 (First week)
Activity 7-11 (Second week)
Activity 1-2 (First week)
Activity 1-2 (Second week)
Activity 11-13 (First week)
Activity 11-13 (Second week)
Activity 4-6
Activity 6-10
Activity 1-4
Activity 1-3
Calculation of total crashing cost:
The total crashing cost is calculated by summing the crashing cost involved all the steps and the indirect costs every week.
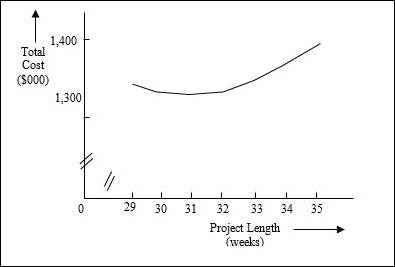
Summarization of total costs for different project lengths:
| Project Length | Cumulative Weeks shortened | Cumulative crash cost ($000) | Indirect cost ($000) | Total cost ($000) |
| A | B | C |
|
E = C+D |
| 35 | 0 | $ - | $ 1,400.00 | $ 1,400.00 |
| 34 | 1 | $ 15.00 | $ 1,360.00 | $ 1,375.00 |
| 33 | 2 | $ 33.00 | $ 1,320.00 | $ 1,353.00 |
| 32 | 3 | $ 58.00 | $ 1,280.00 | $ 1,338.00 |
| 31 | 4 | $ 96.00 | $ 1,240.00 | $ 1,336.00 |
| 30 | 5 | $ 139.00 | $ 1,200.00 | $ 1,339.00 |
| 29 | 6 | $ 185.00 | $ 1,160.00 | $ 1,345.00 |
Cost curve:
The cost curve is plotted by taking the project length on the X-axis and the total cost on the Y-axis.

Want to see more full solutions like this?
Chapter 17 Solutions
EBK OPERATIONS MANAGEMENT
- Can you guys help me with this? Thank you! Here's the question: Compared to the CONSTRAINT model, how has the network changed? How do you plan to add contingency to your network? Please answer this thoroughly Here's the what-if scenario: Assume that the LA warehouse becomes temporarily or even indefinitely disabled since facing a large-scale labor disruption. Re-optimize the network considering this new constraint. Here's the scenario comparison analysis: Scenario Constraint Scenario vs What-if Scenario Summary The Constraint Scenario exhibits a higher total cost of $7,424,575.45 compared to the What-if Scenario's total cost of $6,611,905.60, signifying a difference of approximately $812,669.85, which indicates a more expensive operation in the Constraint Scenario. The average service time is slightly higher in the Constraint Scenario (0.72 days vs. 0.70 days), suggesting that the What-if Scenario provides a marginally quicker service. Moreover, the average end-to-end service time…arrow_forwardCan you guys help me with this? Thank you! Here's the question: Compared to the CONSTRAINT model, how has the network changed? How do you plan to add contingency to your network? Please answer this throughly Here's the what-if scenario: Assume that Dallas plant has lost power. It cannot serve the DCs anymore and has to remain locked indefinitely. Re-optimize the network considering this new constraint. Here's the scenario comparison analysis: Scenario Constraint Scenario vs What-if Scenario Summary In comparing the Constraint Scenario to the What-if Scenario, a few key differences highlight the efficiencies evident in the supply chain. Firstly, the total cost in the Constraint Scenario is lower at $7,424,575.45, while the What-if Scenario incurs a total cost of $7,486,369.12, resulting in a cost delta of $61,793.67. Additionally, although both scenarios exhibit the same average service time of 0.72 days, the What-if Scenario has a more favorable average end-to-end service time of 2.41…arrow_forwardEmployee In-Service Training ASSIGNMENT: In-Service Training. The intern is required to plan and implement two in-service training sessions for employees. Each in-service should last at least 10 but not more than 30 minutes and should be given to all employees affected. The preceptor or supervisor/unit manager must approve all in-service topics. 1) One presentation should be related to a policy or procedure of any kind (e.g. proper use of equipment); 2) The second presentation must be related to sanitation or safety. For each in-service presentation, the intern must develop a written class plan and a visual aid (may be a handout, poster, PowerPoint slide presentation, etc.) appropriate to the life experiences, cultural diversity and educational background of the target audience. The intern must also measure behavior change. Note, this cannot be measured by a written pre- and post- test. That would be measuring knowledge. The intern mustactually observe and document that the learners…arrow_forward
- A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process – assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120 while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. Linear programming is to be used to develop a production schedule. Define the variables as follows: T = number of tables produced each week C= number of chairs produced each week According to the above information, what would the objective function be? (a) Maximize T+C (b) Maximize 120T + 80C (c) Maximize 200T+200C (d) Minimize 6T+5C (e) none of the above According to the information provided in Question 17, which of the following would be a necessary constraint in the problem? (a) T+C ≤ 40 (b) T+C ≤ 200 (c) T+C ≤ 180 (d) 120T+80C ≥ 1000…arrow_forwardAs much detail as possible. Dietary Management- Nursing Home Don't add any fill-in-the-blanksarrow_forwardMenu Planning Instructions Use the following questions and points as a guide to completing this assignment. The report should be typed. Give a copy to the facility preceptor. Submit a copy in your Foodservice System Management weekly submission. 1. Are there any federal regulations and state statutes or rules with which they must comply? Ask preceptor about regulations that could prescribe a certain amount of food that must be kept on hand for emergencies, etc. Is the facility accredited by any agency such as Joint Commission? 2. Describe the kind of menu the facility uses (may include standard select menu, menu specific to station, non-select, select, room service, etc.) 3. What type of foodservice does the facility have? This could be various stations to choose from, self-serve, 4. conventional, cook-chill, assembly-serve, etc. Are there things about the facility or system that place a constraint on the menu to be served? Consider how patients/guests are served (e.g. do they serve…arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,


