
Concept explainers
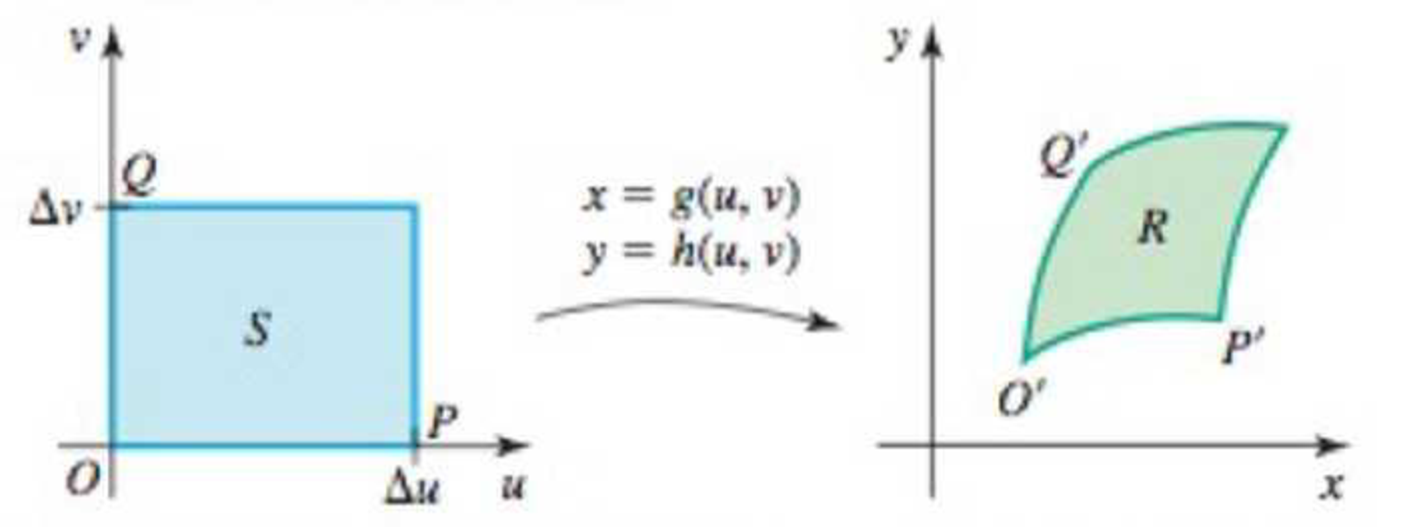
Meaning of the Jacobian The Jacobian is a magnification (or reduction) factor that relates the area of a small region near the point (u, v) to the area of the image of that region near the point (x,y).
a. Suppose S is a rectangle in the uv-plane with vertices O(0,0), P(Δu, 0), {Δu, Δv), and Q(0, Δv) (see figure). The image of S under the transformation x = g(u, v), y = h(u, v) is a region R in the xy-plane. Let O’ P’ and Q’ be the images of O, P, and Q, respectively, in the xy-plane, where O’ P’ and Q’ do not all lie on the same line. Explain why the coordinates of O’, P’, and Q’ are (g(0, 0), h(0, 0)), (g(Δu, 0), h(Δu, 0)), and (g(0, Δv), h(0, Δv)), respectively.
b. Use a Taylor series in both variables to show that
where gu (0,0) is
c. Consider the
d. Explain why the ratio of the area of R to the area of S is approximately |J(u, v)|.
Want to see the full answer?
Check out a sample textbook solution
Chapter 16 Solutions
Calculus Early Transcendentals 3rd.edition I.r.c.
Additional Math Textbook Solutions
College Algebra (7th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
College Algebra with Modeling & Visualization (5th Edition)
Pre-Algebra Student Edition
Algebra and Trigonometry (6th Edition)
Calculus: Early Transcendentals (2nd Edition)
- 17. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.2.050. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) du 4√3- -4² Need Help? Read It SUBMIT ANSWER 18. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.2.051. Evaluate the integral. (Use C for the constant of integration.) - 49 dx x² +3 Need Help? Read It Watch It SUBMIT ANSWER 19. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.2.057. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) 25+ x2 dxarrow_forwardLet (5,3,-7) and = (2, -3, -6). = Compute the following: u× u = -4(u xv) ux (-4v) (+v) × v=arrow_forwardLet a = (4, -2, -7) and 6 = (2,5, 3). (ã − ò) × (ã + b) =arrow_forward
- Use the graph of the function y = f (x) to find the value, if possible. f(x) 8 7 6 Q5 y 3 2 1 x -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 -1 -2 -3 -4 -5 -6 -7 -8+ Olim f(z) x-1+ O Limit does not exist.arrow_forwardIf h(x) = -2x-8 49x2-9 what is lim h(x)? x--00arrow_forwardQuestion Find the following limit. Select the correct answer below: ○ 0 ○ 3 ○ 6 ∞ 6x + 3e lim 00+2 x 2arrow_forward
- What is the limit as x → ∞ of t(x) = = √81x2 -3x+5arrow_forwardConsider the graphs of y = f(x) and y = g(x) in the given diagram y= f(x). y = g(x) Evaluate (f+g)(2) -5 Determine all for which g(x) < f(x) Determine all for which f(x) +3 = g(x)arrow_forwardI) For what value(s) of x does g(x) = -4? Separate multiple answers with commas as needed. J) Give the interval(s) of such that g(x) > 0. Use the union symbol between multiple intervals. K) Give the interval(s) of such that g(x) <0. Use the union symbol between multiple intervals.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,

