Chapter 16, Problem 78P

In a cylindrical pipe where area isn’t constant. Equation 16.5 takes the form H = −kA(dT/dr), where r is the radial coordinate measured from the pipe axis. Use this equation to show that the heat-loss rate from a cylindrical pipe of radius R₁ and length L is

$H=\frac{2\text{πkL}({\text{T}}_1-{\text{T}}_2)}{\ln ({\text{R}}_2/{\text{R}}_1)}$

where the pipe is surrounded by insulation of outer radius R₂ and thermal conductivity k and where T₁ and T₂ are the temperatures at the pipe surface and the outer surface of the insulation, respectively. (Hint: Consider the heat flow through a thin section of pipe, with thickness dr, as shown in Fig. 16.16. Then integrate.)

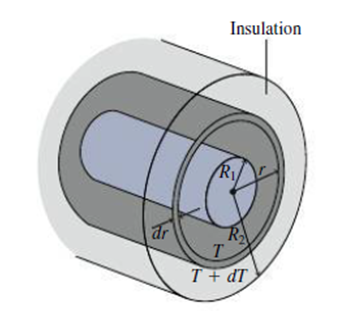
Figure 16.16 Problem 76