
Refer to the Baseball 2012 data, which report information on the 2012 Major League Baseball season.
- a. Rank the teams by the number of wins and their total team salary. Compute the coefficient of rank
correlation between the two variables. At the .01 significance level, can you conclude that it is greater than zero? - b. Assume that the distributions of team salaries for the American League and National League do not follow the
normal distribution . Conduct a test of hypothesis to see whether there is a difference in the two distributions. - c. Rank the 30 teams by attendance and by team salary. Determine the coefficient of rank correlation between these two variables. At the .05 significance level, is it reasonable to conclude the ranks of these two variables are related?
a.
Find the rank correlation coefficient between the number of Wins and total team salary.
Conduct a hypothesis test to see whether the rank correlation is greater than zero.
Answer to Problem 42DE
The rank correlation coefficient between the number of Wins and team salary is 0.105.
Explanation of Solution
Step-by-step procedure to obtain the rank correlation using Minitab software:
- Select Stat > Basic Statistics > Correlation.
- In Variables, select Wins, and team salary from the box on the left.
- Click OK.
Output obtained using Minitab is as follows:

Thus, the rank correlation coefficient between the number of Wins and team salary is 0.105.
Denote the population correlation as
The null and alternative hypotheses are stated as follows:
Null hypothesis:
That is, the correlation between the ranks of the number of wins and team salary.
Alternative hypothesis:
That is, there is positive correlation in the ranks of the number of wins and team salary.
Test statistic:
The test statistic is as follows:
Here, sample size is 30 and correlation coefficient is 0.105.
The test statistic is computed as follows:
Thus, the test statistic value is 0.559.
Degrees of freedom:
The level of significance is 0.01.
Step-by-step software procedure to obtain the critical value using EXCEL software is as follows:
- Open an EXCEL file.
- In cell A1, enter the formula “=T.INV (0.01, 12)”.
Output using the EXCEL is given as follows:
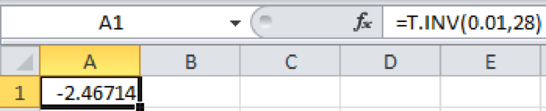
From the EXCEL output, the critical value for the right tailed test is 2.467
Decision rule:
Reject the null hypothesis H0 if,
Otherwise fail to reject H0.
Conclusion:
The value of test statistic is 0.559 and critical value is 2.467.
Here,
By the rejection rule, fail to reject the null hypothesis at the 0.01 significance level.
Thus, there is no sufficient evidence to conclude that there is a positive correlation in the ranks of the number of wins and team salary.
b.
Conduct a test of hypothesis to see whether there is a difference in the distribution of team salaries for the American League and National League.
Answer to Problem 42DE
There is no difference in the distributions of the team salaries for the American League and National League.
Explanation of Solution
The Mann-Whitney test is suitable for the comparison of two inpendent groups.
The null and alternative hypotheses are stated as follows:
Null hypothesis: There is no difference in the distributions of the team salaries for the American League and National League.
Alternative hypothesis: There is a difference in the distributions of the team salaries for the American League and National League.
Step-by-step procedure to obtain the test statistic using Excel MegaStat software is as follows:
- Choose MegaStat > Nonparametric Tests > Wilcoxon – Mann/Whitney Test.
- In Group 1, enter the column of American League.
- In Group 2, enter the second column of National League.
- Select on Continuity correction and Select the Alternative.
- Click OK
Output obtained using Excel Mega stat software is as follows:
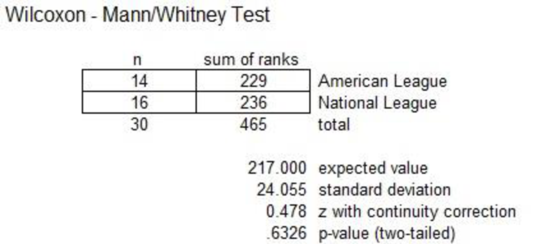
From the above output, the value of the test statistic is 0.478 and the p-value is 0.6326.
Conclusion:
Consider the significance level is 0.05.
Here, the p-value is greater than the significance level 0.05.
By the rejection rule, fail to reject the null hypothesis at the 0.05 significance level.
Therefore, there is no difference in the distributions of the team salaries for the American League and National League.
c.
Find the coefficient of rank correlation between attendance and team salary.
Check whether it is reasonable to conclude the ranks of these two variables are related.
Answer to Problem 42DE
The coefficient of rank correlation between attendance and team salary is 0.805.
Explanation of Solution
Step-by-step procedure to obtain the rank correlation using Minitab software:
- Select Stat > Basic Statistics > Correlation.
- In Variables, select Attendance, and team salary from the box on the left.
- Click OK.
Output obtained using Minitab is as follows:

From the above output, the coefficient of rank correlation between attendance and team salary is 0.805.
Denote the population correlation as
The null and alternative hypotheses are stated below:
Null hypothesis:
That is, there is no correlation between attendance and team salary.
Alternative hypothesis:
That is, there is a correlation between attendance and team salary.
Here, sample size is 30 and correlation coefficient is 0.805.
The test statistic is as follows:
Thus, the test statistic value is 7.18.
Degrees of freedom:
The level of significance is 0.05.
Step-by-step software procedure to obtain the critical value using EXCEL software is as follows:
- Open an EXCEL file.
- In cell A1, enter the formula “=T.INV.2T (0.05, 28)”.
Output using the EXCEL is given as follows:

From the EXCEL output, the critical value is 2.048
Conclusion:
The value of test statistic is 7.18 and critical value is 2.048.
Here,
By the rejection rule, reject the null hypothesis at the 0.05 significance level.
Therefore, it is reasonable to conclude that the ranks of these two variables are related.
Want to see more full solutions like this?
Chapter 16 Solutions
Statistical Techniques in Business and Economics
- Please answer the questionsarrow_forward30. An individual who has automobile insurance from a certain company is randomly selected. Let Y be the num- ber of moving violations for which the individual was cited during the last 3 years. The pmf of Y isy | 1 2 4 8 16p(y) | .05 .10 .35 .40 .10 a.Compute E(Y).b. Suppose an individual with Y violations incurs a surcharge of $100Y^2. Calculate the expected amount of the surcharge.arrow_forward24. An insurance company offers its policyholders a num- ber of different premium payment options. For a ran- domly selected policyholder, let X = the number of months between successive payments. The cdf of X is as follows: F(x)=0.00 : x < 10.30 : 1≤x<30.40 : 3≤ x < 40.45 : 4≤ x <60.60 : 6≤ x < 121.00 : 12≤ x a. What is the pmf of X?b. Using just the cdf, compute P(3≤ X ≤6) and P(4≤ X).arrow_forward
- 59. At a certain gas station, 40% of the customers use regular gas (A1), 35% use plus gas (A2), and 25% use premium (A3). Of those customers using regular gas, only 30% fill their tanks (event B). Of those customers using plus, 60% fill their tanks, whereas of those using premium, 50% fill their tanks.a. What is the probability that the next customer will request plus gas and fill the tank (A2 B)?b. What is the probability that the next customer fills the tank?c. If the next customer fills the tank, what is the probability that regular gas is requested? Plus? Premium?arrow_forward38. Possible values of X, the number of components in a system submitted for repair that must be replaced, are 1, 2, 3, and 4 with corresponding probabilities .15, .35, .35, and .15, respectively. a. Calculate E(X) and then E(5 - X).b. Would the repair facility be better off charging a flat fee of $75 or else the amount $[150/(5 - X)]? [Note: It is not generally true that E(c/Y) = c/E(Y).]arrow_forward74. The proportions of blood phenotypes in the U.S. popula- tion are as follows:A B AB O .40 .11 .04 .45 Assuming that the phenotypes of two randomly selected individuals are independent of one another, what is the probability that both phenotypes are O? What is the probability that the phenotypes of two randomly selected individuals match?arrow_forward
- 53. A certain shop repairs both audio and video compo- nents. Let A denote the event that the next component brought in for repair is an audio component, and let B be the event that the next component is a compact disc player (so the event B is contained in A). Suppose that P(A) = .6 and P(B) = .05. What is P(BA)?arrow_forward26. A certain system can experience three different types of defects. Let A;(i = 1,2,3) denote the event that the sys- tem has a defect of type i. Suppose thatP(A1) = .12 P(A) = .07 P(A) = .05P(A, U A2) = .13P(A, U A3) = .14P(A2 U A3) = .10P(A, A2 A3) = .011Rshelfa. What is the probability that the system does not havea type 1 defect?b. What is the probability that the system has both type 1 and type 2 defects?c. What is the probability that the system has both type 1 and type 2 defects but not a type 3 defect? d. What is the probability that the system has at most two of these defects?arrow_forwardThe following are suggested designs for group sequential studies. Using PROCSEQDESIGN, provide the following for the design O’Brien Fleming and Pocock.• The critical boundary values for each analysis of the data• The expected sample sizes at each interim analysisAssume the standardized Z score method for calculating boundaries.Investigators are evaluating the success rate of a novel drug for treating a certain type ofbacterial wound infection. Since no existing treatment exists, they have planned a one-armstudy. They wish to test whether the success rate of the drug is better than 50%, whichthey have defined as the null success rate. Preliminary testing has estimated the successrate of the drug at 55%. The investigators are eager to get the drug into production andwould like to plan for 9 interim analyses (10 analyzes in total) of the data. Assume thesignificance level is 5% and power is 90%.Besides, draw a combined boundary plot (OBF, POC, and HP)arrow_forward
- Please provide the solution for the attached image in detailed.arrow_forward20 km, because GISS Worksheet 10 Jesse runs a small business selling and delivering mealie meal to the spaza shops. He charges a fixed rate of R80, 00 for delivery and then R15, 50 for each packet of mealle meal he delivers. The table below helps him to calculate what to charge his customers. 10 20 30 40 50 Packets of mealie meal (m) Total costs in Rands 80 235 390 545 700 855 (c) 10.1. Define the following terms: 10.1.1. Independent Variables 10.1.2. Dependent Variables 10.2. 10.3. 10.4. 10.5. Determine the independent and dependent variables. Are the variables in this scenario discrete or continuous values? Explain What shape do you expect the graph to be? Why? Draw a graph on the graph provided to represent the information in the table above. TOTAL COST OF PACKETS OF MEALIE MEAL 900 800 700 600 COST (R) 500 400 300 200 100 0 10 20 30 40 60 NUMBER OF PACKETS OF MEALIE MEALarrow_forwardLet X be a random variable with support SX = {−3, 0.5, 3, −2.5, 3.5}. Part ofits probability mass function (PMF) is given bypX(−3) = 0.15, pX(−2.5) = 0.3, pX(3) = 0.2, pX(3.5) = 0.15.(a) Find pX(0.5).(b) Find the cumulative distribution function (CDF), FX(x), of X.1(c) Sketch the graph of FX(x).arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt


