Chapter 16, Problem 2SP

(a)

To determine

The position of first bright fringe appears on either side of the central fringe.

Answer to Problem 2SP

The position of first bright fringe is $36\text{mm}$ away from the center at each side.

Explanation of Solution

Given info: Wavelength of the light is $640\text{nm}$, order of bright fringe is 1, the distance of screen from slits is $1.8\text{m}$ and spacing between adjacent slits is $0.032\text{mm}$.

Write an expression for condition of maxima.

$y=\frac{n\lambda D}{d}$

Here,

$y$ is the distance of nth bright fringe from center

$n$ is the order of the bright fringe

$D$ is the screen’s distance from slit

$\lambda$ is the wavelength

$d$ is the slit separation

Substitute $580\text{nm}$ for $\lambda$, $1$ for $n$, $1.3\text{m}$ for $D$ and $0.044\text{mm}$ for $d$ to find $y$.

$\begin{array}{c}y=\frac{\left(1\right)\left(\left(640\text{nm}\right)\left(\frac{1\text{m}}{{10}^{-9}\text{nm}}\right)\right)\left(1.8\text{m}\right)}{\left(0.032\text{mm}\right)\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)}\\ =36\times {10}^{-3}\text{m}\\ =\left(36\times {10}^{-3}\text{m}\right)\left(\frac{1\text{mm}}{{10}^{-3}\text{m}}\right)\\ =36\text{mm}\end{array}$

Thus, the position of first bright fringe is $36\text{mm}$ away from the center at each side of the central maxima.

Conclusion:

Thus, position of first bright fringe is $36\text{mm}$ away from the center at each side of the central fringe.

(b)

To determine

The position of second bright fringe on either side of the central fringe.

Answer to Problem 2SP

The position of second bright fringe is $72\text{mm}$ away from the center at each side of the central fringe.

Explanation of Solution

Given info: Wavelength of the light is $640\text{nm}$, order of bright fringe is 2, the distance of screen from slits is $1.8\text{m}$ and spacing between adjacent slits is $0.032\text{mm}$.

Write an expression for condition of maxima.

$y=\frac{n\lambda D}{d}$

Here,

$y$ is the distance of nth bright fringe from center

$n$ is the order of the bright fringe

$D$ is the screen’s distance from slit

$\lambda$ is the wavelength

$d$ is the slit separation

Substitute $640\text{nm}$ for $\lambda$, $2$ for $n$, $1.8\text{m}$ for $D$ and $0.032\text{mm}$ for $d$ to find $y$.

$\begin{array}{c}y=\frac{\left(2\right)\left(\left(640\text{nm}\right)\left(\frac{1\text{m}}{{10}^{-9}\text{nm}}\right)\right)\left(1.8\text{m}\right)}{\left(0.032\text{mm}\right)\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)}\\ =72\times {10}^{-3}\text{m}\\ =\left(72\times {10}^{-3}\text{m}\right)\left(\frac{1\text{mm}}{{10}^{-3}\text{m}}\right)\\ =72\text{mm}\end{array}$

Thus, the position of second bright fringe is $72\text{mm}$ away from the center at each side of the central fringe.

Conclusion:

The position of second bright fringe is $72\text{mm}$ away from the center at each side of the central fringe.

(c)

To determine

The position of first dark bright fringe appeared on either side of the central fringe.

Answer to Problem 2SP

The position of first dark fringe is $54\text{mm}$ away from the center at each side of the central fringe.

Explanation of Solution

Given info: Wavelength of the light is $640\text{nm}$, order of dark fringe is 1, the distance of screen from slits is $1.8\text{m}$ and spacing between adjacent slits is $0.032\text{mm}$.

Write an expression for condition of minima.

$y=\left(n+\frac{1}{2}\right)\frac{\lambda D}{d}$

Here,

$y$ is the distance of nth dark fringe from center

$n$ is the order of the bright fringe

$D$ is the screen’s distance from slit

$\lambda$ is the wavelength

$d$ is the slit separation

Substitute $640\text{nm}$ for $\lambda$, $1$ for $n$, $1.8\text{m}$ for $D$ and $0.032\text{mm}$ for $d$ to find $y$.

$\begin{array}{c}y=\left(1+\frac{1}{2}\right)\frac{\left(\left(640\text{nm}\right)\left(\frac{1\text{m}}{{10}^{-9}\text{nm}}\right)\right)\left(1.8\text{m}\right)}{\left(0.032\text{mm}\right)\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)}\\ =54\times {10}^{-3}\text{m}\\ =\left(54\times {10}^{-3}\text{m}\right)\left(\frac{1\text{mm}}{{10}^{-3}\text{m}}\right)\\ =54\text{mm}\end{array}$

Thus, the position of first dark fringe is $54\text{mm}$ away from the center at each side.

Conclusion:

Thus, position of first dark fringe is $54\text{mm}$ away from the center at each side.

(d)

To determine

Sketch the diffraction pattern showing the position of the seven central fringes and mark the position of the fringes.

Answer to Problem 2SP

The diffraction pattern is given in figure 1.

Explanation of Solution

Write an expression for condition of minima.

$y=\left(n+\frac{1}{2}\right)\frac{\lambda D}{d}$

Here,

$y$ is the distance of nth dark fringe from center

$n$ is the order of the dark fringe

$D$ is the screen’s distance from slit

$\lambda$ is the wavelength

$d$ is the slit separation

Substitute $640\text{nm}$ for $\lambda$, $2$ for $n$, $1.8\text{m}$ for $D$ and $0.032\text{mm}$ for $d$ to find $y$.

$\begin{array}{c}y=\left(1+\frac{1}{2}\right)\frac{\left(\left(640\text{nm}\right)\left(\frac{1\text{m}}{{10}^{-9}\text{nm}}\right)\right)\left(1.8\text{m}\right)}{\left(0.032\text{mm}\right)\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)}\\ =90\times {10}^{-3}\text{m}\\ =\left(90\times {10}^{-3}\text{m}\right)\left(\frac{1\text{mm}}{{10}^{-3}\text{m}}\right)\\ =90\text{mm}\end{array}$

Thus, the position of second dark fringe is $90\text{mm}$ away from the center at each side.

Write an expression for condition of maxima.

$y=\frac{n\lambda D}{d}$

Here,

$y$ is the distance of nth bright fringe from center

$n$ is the order of the bright fringe

$D$ is the screen’s distance from slit

$\lambda$ is the wavelength

$d$ is the slit separation

Substitute $640\text{nm}$ for $\lambda$, 3 for $n$, $1.8\text{m}$ for $D$ and $0.032\text{mm}$ for $d$ to find $y$.

$\begin{array}{c}y=\frac{\left(3\right)\left(\left(640\text{nm}\right)\left(\frac{1\text{m}}{{10}^{-9}\text{nm}}\right)\right)\left(1.8\text{m}\right)}{\left(0.032\text{mm}\right)\left(\frac{1\text{m}}{{10}^3\text{mm}}\right)}\\ =108\times {10}^{-3}\text{m}\\ =\left(108\times {10}^{-3}\text{m}\right)\left(\frac{1\text{mm}}{{10}^{-3}\text{m}}\right)\\ =108\text{mm}\end{array}$

Thus, the position of third bright fringe is $108\text{mm}$ away from the center at each side of the central fringe.

Following figure gives the diffraction pattern.

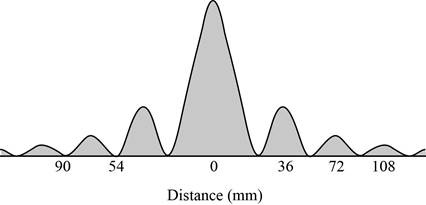
Figure 1

Here, the first, second and third order bright fringes will appear at distance of $36\text{mm}$, $72\text{mm}$ and $108\text{mm}$ from center respectively at each side of the central maxima. The dark fringes of order 1 and 2 will form distances $54\text{mm}$ and $90\text{mm}$ respectively.

Conclusion:

The diffraction pattern is given in figure 1.