
Concept explainers
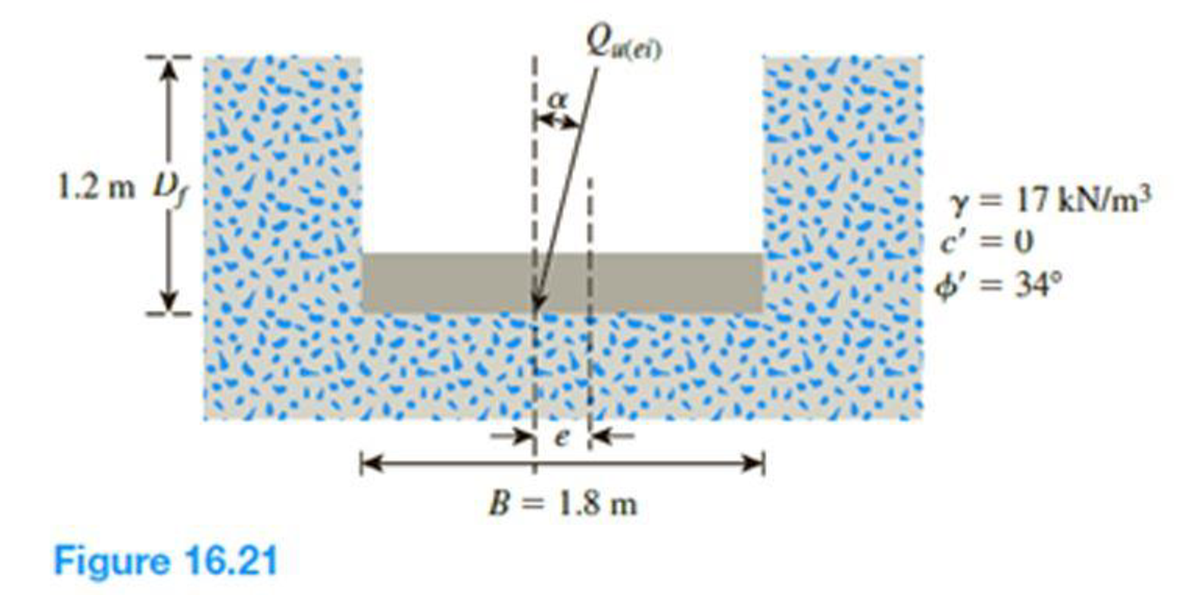
Figure 16.21 shows a continuous foundation with a width of 1.8 m constructed at a depth of 1.2 m in a granular soil. The footing is subjected to an eccentrically inclined loading with e = 0.3 m, and α = 10°. Determine the gross ultimate load, Qu(ei), that the footing can support using:
- a. Meyerhof (1963) method [Eq. (16.52)]
- b. Saran and Agarwal (1991) method [Eq. (16.53)]
- c. Patra et al. (2012) reduction factor method [Eq. (16.54)]
(a)
The gross ultimate load Qu(ei) that the footing can support by using Meyerhof method.
Answer to Problem 16.19P
The gross ultimate load Qu(ei) that the footing can support by using Meyerhof method is 984 kN/m_.
Explanation of Solution
Given information:
The unit weight of the soil γ is 17 kN/m3.
The value of cohesion c′ is 0.
The soil friction angle ϕ′ is 34°.
The location of depth of footing base Df is 1.2 m.
The width of the footing B is 1.8 m.
The value of eccentricity e is 0.3 m.
The inclined angle α is 10°.
Calculation:
Determine the effective width of the footing using the relation.
B′=B−2e
Substitute 1.8 m for B and 0.3 for e.
B′=1.8−2×0.3=1.2 m
For the continuous foundation, all shape factors are equal to one (λcs=λqs=λγs=1.0).
Determine the depth factor λcd using the relation.
λcd=1+0.4tan−1(DfB′)
Substitute 1.2 m for Df and 1.2 m for B′.
λcd=1+0.4(1.21.2)=1.4
Determine the depth factor λqd using the relation.
λqd=1+2tanϕ′(1−sinϕ′)2(DfB′)
Substitute 34° for ϕ′, 1.2 m for Df, and 1.2 m for B′.
λqd=1+2tan34°(1−sin34°)2(1.21.2)=1.262
Determine the inclination factor λqi using the relation.
λqi=(1−α90°)2
Substitute 10° for α.
λqi=(1−10°90°)2=0.79
Determine the inclination factor λγi using the relation.
λγi=(1−αϕ′)2
Substitute 10° for α and 34° for ϕ′.
λγi=(1−10°34°)2=0.498
Determine the ultimate bearing capacity of the soil (q′u) using the relation.
q′u=c′Ncλcsλcd+qNqλqsλqd+12γB′Nγλγsλγd=c′Ncλcsλcd+γDfNqλqsλqd+12γB′Nγλγsλγd (1)
Here, λγd is the depth factor and Nc, Nq, and Nγ are bearing-capacity factors.
Refer Table 16.2, “Bearing-capacity factors Nc, Nq, and Nγ” in the textbook.
For ϕ′=34°;
The values of Nc is 42.16, Nq is 29.44, and Nγ is 41.06.
Substitute 0 for c′, 42.16 for Nc, 1.0 for λcs, 1.4 for λcd, 17 kN/m3 for γ, 1.2 m for Df, 29.44 for Nq, 1.0 for λqs, 1.262 for λqd, 0.79 for λqi, 1.2 m for B′, 41.06 for Nγ, 1.0 for λγs, 1.0 for λγd, and 0.498 for λγi in Equation (1).
q′u={(0×42.16×1.0×1.4)+(17×1.2×29.44×1.0×1.262×0.79)+(12×17×1.2×41.06×1×1×0.498)}=807.33 kN/m2
Determine the gross ultimate load Qu(ei) using the relation.
Qu(ei)=q′uB′cosα
Substitute 807.33 kN/m2 for q′u, 1.2 m for B′, and 10° for α.
Qu(ei)=807.33×1.2cos10°=984 kN/m
Therefore, the gross ultimate load Qu(ei) that the footing can support by using Meyerhof method is 984 kN/m_.
(b)
The gross ultimate load Qu(ei) that the footing can support by using Saran and Agarwal method.
Answer to Problem 16.19P
The gross ultimate load Qu(ei) that the footing can support by using Saran and Agarwal method is 1,237 kN/m_.
Explanation of Solution
Given information:
The unit weight of the soil γ is 17 kN/m3.
The value of cohesion c′ is 0.
The soil friction angle ϕ′ is 34°.
The location of depth of footing base Df is 1.2 m.
The width of the footing B is 1.8 m.
The value of eccentricity e is 0.3 m.
The inclined angle α is 10°.
Calculation:
Determine the ratio of (eB).
Substitute 0.3 for e and 1.8 m for B.
(eB)=0.31.8=0.167
Determine the gross ultimate load Qu(ei) using the relation.
Qu(ei)=B[c′Nc(ei)+qNq(ei)+12γBNγ(ei)]=B[c′Nc(ei)+γDfNq(ei)+12γBNγ(ei)] (2)
Here, Nc(ei), Nq(ei), and Nγ(ei) are the bearing capacity factors.
Refer Figure 16.14, “Variation of Nc(ei)-(b)” in the textbook.
Take the Nc(ei) value as 24.0 for ϕ′ value of 34° and the (eB) value of 0.167.
Refer Figure 16.15, “Variation of Nq(ei)-(b)” in the textbook.
Take the Nq(ei) value as 22.8 for ϕ′ value of 34° and the (eB) value of 0.167.
Refer Figure 16.16, “Variation of Nγ(ei)-(b)” in the textbook.
Take the Nγ(ei) value as 14.5 for ϕ′ value of 34° and the (eB) value of 0.167.
Substitute 0 for c′, 24.0 for Nc(ei), 17 kN/m3 for γ, 1.2 m for Df, 22.8 for Nq(ei), 1.8 m for B, and 14.5 for Nγ(ei), in Equation (2).
Qu(ei)=1.8(0×24.0+17×1.2×22.8+12×17×1.8×14.5)=1,237 kN/m
Therefore, the gross ultimate load Qu(ei) that the footing can support by using Saran and Agarwal method is 1,237 kN/m_.
(c)
The gross ultimate load Qu(ei) that the footing can support by using Patra et al. reduction factor method.
Answer to Problem 16.19P
The gross ultimate load Qu(ei) that the footing can support by using Patra et al. reduction factor method is 1,006 kN/m_.
Explanation of Solution
Given information:
The unit weight of the soil γ is 17 kN/m3.
The value of cohesion c′ is 0.
The soil friction angle ϕ′ is 34°.
The location of depth of footing base Df is 1.2 m.
The width of the footing B is 1.8 m.
The value of eccentricity e is 0.3 m.
The inclined angle α is 10°.
Calculation:
For the continuous foundation, all shape factors are equal to one (λcs=λqs=λγs=1.0).
Determine the depth factor λcd using the relation.
λcd=1+0.4tan−1(DfB)
Substitute 1.2 m for Df and 1.8 m for B.
λcd=1+0.4(1.21.8)=1.26
Determine the depth factor λqd using the relation.
λqd=1+2tanϕ′(1−sinϕ′)2(DfB)
Substitute 34° for ϕ′, 1.2 m for Df, and 1.8 m for B.
λqd=1+2tan34°(1−sin34°)2(1.21.8)=1.175
Determine the ultimate bearing capacity of the soil (qu) using the relation.
qu=c′Ncλcsλcd+qNqλqsλqd+12γBNγλγsλγd=c′Ncλcsλcd+γDfNqλqsλqd+12γBNγλγsλγd (3)
Refer Table 16.2, “Bearing-capacity factors Nc, Nq, and Nγ” in the textbook.
Take the Nc as 42.16, Nq as 29.44, and Nγ as 41.06 for the ϕ′ value of 34°.
Substitute 0 for c′, 42.16 for Nc, 1.0 for λcs, 1.26 for λcd, 17 kN/m3 for γ, 1.2 m for Df, 29.44 for Nq, 1.0 for λqs, 1.175 for λqd, 1.8 m for B, 41.06 for Nγ, 1.0 for λγs, and 1.0 for λγd, in Equation (3).
qu={0×42.16×1.0×1.26+17×1.2×29.44×1.0×1.175+12×17×1.8×41.06×1×1}=1,333.89 kN/m2
Determine the gross ultimate load Qu(ei) using the relation.
Qu(ei)=Bqu[1−2(eB)](1−αϕ′)2−(Df/B)
Substitute 1.8 m for B, 1,333.89 kN/m2 for q′u, 0.3 m for e, 10° for α, 34° for ϕ′, and 1.2 m for Df.
Qu(ei)=1.8×1,333.89[1−2(0.31.8)](1−10°34°)2−(1.2/1.8)=1,006 kN/m
Therefore, the gross ultimate load Qu(ei) that the footing can support by using Patra et al. reduction factor method is 1,006 kN/m_.
Want to see more full solutions like this?
Chapter 16 Solutions
Principles Of Geotechnical Engineering, Si Edition
- From station A with center height for 1.4m in fill, the ground makes a uniform slope of 5% to station B whose center height is 2.8 m in cut. Assuming both sections to be level sections having a width of roadway of 14 m and a side slope of 2:1 for both cut and fill, compute the cross-sectional area of fill 48 m from station A. Distance from station A to station B is 60 m.arrow_forwardFrom station 10+100 with center heights of 2 m in fill, the ground line makes a uniform slope of 4.8% to station 10+150 whose center heights is 1.2 m in cut. 1. Determine the slope of a new roadway to be constructed. 2. Determine the distance from station 10+150, will the excavation extend. 3. Determine the area of fill 10 m from 10+100 if the width of roadway is 8 m and the side slope is 1:2.arrow_forwardFunding Plan How much funds required to reach to the next level of the venture? • ? How much have been bootstrapped? If not, why? • ? How much can be bootstrapped? • ? How much external funding required? If not, why? • ? Funds utilization strategy (Details) • ? • ? • ? • ? • ? • ? • • ? ? ? ? ? Place your logo herearrow_forward
- A semicircular 40 ft diameter− − tunnel is to be built under a150 ft deep− − , 800 ft long− − lake, as shown below. a) Determine the horizontal, vertical, and resulting hydrostatic forces acting on this tunnel. (Answer: 8 8 8 1.398 10 , 2.596 10 , 2.64 10H y netF lbf F lbf F lbf= × = × = × ) b) Calculate the hydrostatic force on the bottom of the lake if the tunnel was not there, and compare it with the total (resulting) hydrostatic force that you calculated in part (a). (Answer: 8 2.995 10VF lbf= × ) c) As the design engineer of this tunnel would you take the hydrostatic force on the bottom of the lake as a rough estimate of the resulting hydrostatic force acting on this tunnel. Discuss your decision.arrow_forward3.2 Consi parabolic equation (Eq. 3.1) 3.3 Again consider Example 3.4. Does this curve provide sufficient stopping sight distance for a speed of 60 mi/h? -tangent grade with a -1% final mi/h. The station of the 1203 ft. What is the elev 3.4 An equal-tangent crest vertical curve is designed for 70 mi/h. The high point is at elevation 1011.4 ft. The initial grade is +2% and the final grade is -1%. What is the elevation of the PVT? +00? 3.10 An equal-tangent w 2012 (to 2011 AASHTO of 70 mi/h to connec -2.1%. The curve is design speed in th technology has adv design deceleration value used to dev percentage of ol design reaction vehicles have b height is assun roadway obje 3.5 An equal-tangent crest curve has been designed for 70 mi/h to connect a +2% initial grade and a -1% final grade for a new vehicle that has a 3 ft driver's eye height; the curve was designed to avoid an object that is 1 ft high. Standard practical stopping distance design was used but, unlike current design standards,…arrow_forwardFactor of Safety Activity The lap joint is connected by three 20-mm diameter rivets. Assuming that the applied allowable load, P=50kN is distributed equally among the three rivets and a factor of safety of 1.5, find: (a) the failure shear stress in a rivet, and (b) failure bearing stress between the plate and rivet 25 mm 25 mmarrow_forward
- Draw the shear and moment diagrams of the beam CDE showing all calculations. Assume the support at A is a roller and B is a pin. There are fixed connected joints at D and E. Assume P equals 9.6 and w equals 0.36arrow_forwardFind the length of the diagonal on the x-z plane (square root of square of sides). Find angle between the vector F and its projection on x-z (the diagonal defined above). Find Horizontal Projection of F on x-z plane, Fh, and vertical component, FY. Find projections of Fh, to define in-plane components Fx and Fz. Show that results match those of Problem 2(a) above. (2,0,4) F₂ 100 N (5, 1, 1)arrow_forwardFor the control system Draw Nyquist Plot with Solution G(S)= 63.625 (S+1)(S+3) S(S+2)(5+65+18) (5+5)arrow_forward
- Q3: Find the support reactions at A: y mm A P=last 2 student's ID#+100 (N) 124N last 3 student's ID# (mm) 724mm 20 mm D B C X last 3 student's ID#+20 mm 744mm 40 mm 60 mmarrow_forwardA hoist trolley is subjected to the three forces shown. Knowing that α = 40°, determine (a) the required magnitude of the force P if the resultant of the three forces is to be vertical, (b) the corresponding magnißide of the resultant. α 724lb last 3 student's ID# lb α last 2 student's ID#+100 lb 124lb Parrow_forwardFive wood boards are bolted together to form the built-up beam shown in the figure. The beam is subjected to a shear force of V = 13 kips. Each bolt has a shear strength of Vbolt = 6 kips. [h₁ =4.25 in., t₁ = 0.5 in., h₂ = 6 in., t₂ = 1 in.] hi + hi/2 h:/2 h: 2 h + h/2 Determine the moment of inertia of the section. Determine the maximum allowable spacing of the bolts. Determine the shear flow in the section connected by fasteners.arrow_forward
 Principles of Geotechnical Engineering (MindTap C...Civil EngineeringISBN:9781305970939Author:Braja M. Das, Khaled SobhanPublisher:Cengage Learning
Principles of Geotechnical Engineering (MindTap C...Civil EngineeringISBN:9781305970939Author:Braja M. Das, Khaled SobhanPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning Fundamentals of Geotechnical Engineering (MindTap...Civil EngineeringISBN:9781305635180Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Fundamentals of Geotechnical Engineering (MindTap...Civil EngineeringISBN:9781305635180Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning



