
Concept explainers
Show that the Fourier coefficients of the triangular wave of Figure 16.7 are zero for n even and (−1)m32(2m+1)2π2(1−cos(2m+1)π8) for n odd.
Answer to Problem 16.10P
Showed that the Fourier coefficients of the triangular wave of Figure 16.7 are zero for n even and (−1)m32(2m+1)2π2(1−cos(2m+1)π8) for n odd.
Explanation of Solution
Consider the Figure shown below.
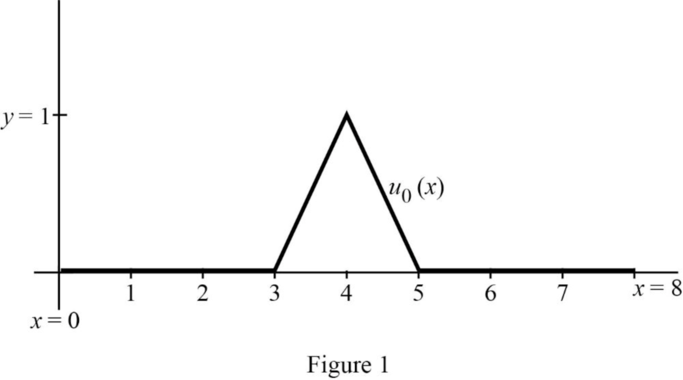
From the Figure, it is clear that, u0(x)=0 for 0<x<3&5<x<8, u0(x) is increasing in the interval x=3 to 4 from 0 to1, and decreasing from 1 to 0 in the interval x=4 to 5.
Write the equation 16.33.
Bn=2LL∫0u0(x)sinnπxLdx (I)
Divide the integral into four parts, use 8 for L, and solve.
Bn=28[3∫0u0(x)sinnπx8dx+4∫3u0(x)sinnπx8dx+5∫4u0(x)sinnπx8dx+8∫5u0(x)sinnπx8dx]=14[0+4∫3u0(x)sinnπx8dx+5∫4u0(x)sinnπx8dx+0]=14[4∫3u0(x)sinnπx8dx+5∫4u0(x)sinnπx8dx] (II)
Consider the enlarged view of triangle in the Figure 1 is shown below.
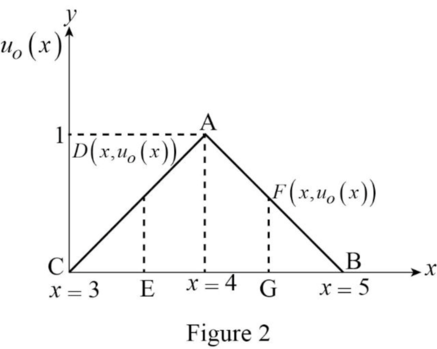
Let D is a point on straight line CA, the coordinate of this point is (x,uo(x)), E is the foot of the perpendicular of D on CB, then the triangle CAH of CDE are similar triangles. So the ratio of corresponding sides of the two triangles are equal.
DEAH=CECH (III)
From the Figure 2, use u0(x) for DE, 1 for AH, x−3 for CE, and 1 for CH.
u0(x)1=x−31u0(x)=x−3 for 3<x<4 (IV)
Let F is a point on straight line AB, the coordinate of this point is (x,uo(x)), G is the foot of the perpendicular of F on CB, then the triangle AHB of FGB are similar triangles. So the ratio of corresponding sides of the two triangles are equal.
FGAH=GBHB (V)
From the Figure 2, use u0(x) for FG, 1 for AH, 5−x for CE, and 1 for CH.
u0(x)1=5−x1u0(x)=5−x for 4<x<5 (VI)
Use equation (IV) and (VI) in the equation (II).
Bn=14[4∫3(x−3)sinnπx8dx+5∫4(5−x)sinnπx8dx] (VII)
Integrate the first part of the equation (VII).
4∫3(x−3)sinnπx8dx=4∫3xsinnπx8dx−34∫3sinnπx8dx={[x(−cosnπx8)nπ8]43−4∫31⋅(−cosnπx8)nπ8}−3[(−cosnπx8)nπ8]43=−8nπ(4cos4nπ8−3cos3nπ8)+8nπ4∫3cosnπx8dx+38nπ(cos4nπ8−cos3nπ8) (VIII)
Solve the equation (VIII).
4∫3(x−3)sinnπx8dx=−32nπcosnπ2+24nπcos3nπ8+8nπ(sin(nπx8)nπ8)43+24nπcosnπ2−24nπcos3nπ8=−8nπcosnπ2+(8nπ)2(sin4nπ8−sin3nπ8)=−8nπcosnπ2+(8nπ)2(sinnπ2−sin3nπ8) (IX)
Integrate the second part of the equation (VII).
4∫3(5−x)sinnπx8dx=5∫45sinnπx8dx−5∫4xsinnπx8dx=[(−cosnπx8)nπ8]54−{[x⋅(−cosnπx8)nπ8]54−5∫41⋅(−cosnπx8)nπ8dx}=−40nπ(cos5nπ8−cos4nπ8)+8nπ(5cos5nπ8−4cos4nπ8)−8nπ5∫4cosnπx8dx (X)
Solve the equation (X).
4∫3(5−x)sinnπx8dx=−40nπcos5nπ2+40nπcosnπ2+40nπcos5nπ8−32nπcosnπ2−8nπ(sin(nπx8)nπ8)54=8nπcosnπ2−(8nπ)2(sin5nπ8−sin4nπ8)=8nπcosnπ2−(8nπ)2(sin5nπ2−sinnπ2) (XI)
Use equation (X) and (XI) in (VII).
Bn=14[−8nπcosnπ2+(8nπ)2(sinnπ2−sin3nπ8)+8nπcosnπ2−(8nπ)2(sin5nπ2−sinnπ2)]=14[(8nπ)2(sinnπ2−sin3nπ8−sin5nπ2+sinnπ2)]=16n2π2(2sinnπ2−sin3nπ8−sin5nπ2)=16n2π2(2sinnπ2−[sin3nπ8+sin5nπ2]) (XII)
Solve equation (XII).
Bn=16n2π2(2sinnπ2−[sin3nπ8+sin5nπ2])=16n2π2(2sinnπ2−2sin(5nπ2+3nπ82)cos(5nπ2−3nπ82))=16n2π2(2sinnπ2−2sinnπ2cosnπ8)=16n2π22sinnπ2(1−cosnπ8)=32n2π2sinnπ2(1−cosnπ8) (XIII)
If n is even, sinnπx2=0, and if n is odd, sinnπx2=(−1)m where m=0,1,2... So equation (XIII) becomes zero for even n. Then the equation (XIII) can be written as for odd n
Bn=(−1)m32(2m+1)2π2[1−cos(2m+1)π8].
Conclusion:
Therefore, the Fourier coefficients of the triangular wave of Figure 16.7 are zero for n even and (−1)m32(2m+1)2π2(1−cos(2m+1)π8) for n odd.
Want to see more full solutions like this?
Chapter 16 Solutions
Classical Mechanics
- A particle with a charge of − 5.20 nC is moving in a uniform magnetic field of (B→=−( 1.22 T )k^. The magnetic force on the particle is measured to be(F→=−( 3.50×10−7 N )i^+( 7.60×10−7 N )j^. Calculate the scalar product v→F→. Work the problem out symbolically first, then plug in numbers after you've simplified the symbolic expression.arrow_forwardNeed help wity equilibrium qestionarrow_forwardneed answer asap please thanks youarrow_forward
- A man slides two boxes up a slope. The two boxes A and B have a mass of 75 kg and 50 kg, respectively. (a) Draw the free body diagram (FBD) of the two crates. (b) Determine the tension in the cable that the man must exert to cause imminent movement from rest of the two boxes. Static friction coefficient USA = 0.25 HSB = 0.35 Kinetic friction coefficient HkA = 0.20 HkB = 0.25 M₁ = 75 kg MB = 50 kg P 35° Figure 3 B 200arrow_forwardA golf ball is struck with a velocity of 20 m/s at point A as shown below (Figure 4). (a) Determine the distance "d" and the time of flight from A to B; (b) Determine the magnitude and the direction of the speed at which the ball strikes the ground at B. 10° V₁ = 20m/s 35º Figure 4 d Barrow_forwardThe rectangular loop of wire shown in the figure (Figure 1) has a mass of 0.18 g per centimeter of length and is pivoted about side ab on a frictionless axis. The current in the wire is 8.5 A in the direction shown. Find the magnitude of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane. Find the direction of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane.arrow_forward
- A particle with a charge of − 5.20 nC is moving in a uniform magnetic field of (B→=−( 1.22 T )k^. The magnetic force on the particle is measured to be (F→=−( 3.50×10−7 N )i^+( 7.60×10−7 N )j^. Calculate the y and z component of the velocity of the particle.arrow_forwardneed answer asap please thank youarrow_forward3. a. Determine the potential difference between points A and B. b. Why does point A have a higher potential energy? Q = +1.0 C 3.2 cm 4.8 cm Aarrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





