Calculus Early Transcendentals 3rd.edition I.r.c.
Calculus Early Transcendentals 3rd.edition I.r.c.
3rd Edition
ISBN: 9780134766843
Author: Briggs
Publisher: PEARSON
bartleby

Concept explainers

Minimization
In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…
Maxima and Minima
The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.
Derivatives
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …
Concavity
In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …
bartleby

Videos

Textbook Question
Book Icon
Chapter 15.3, Problem 86E

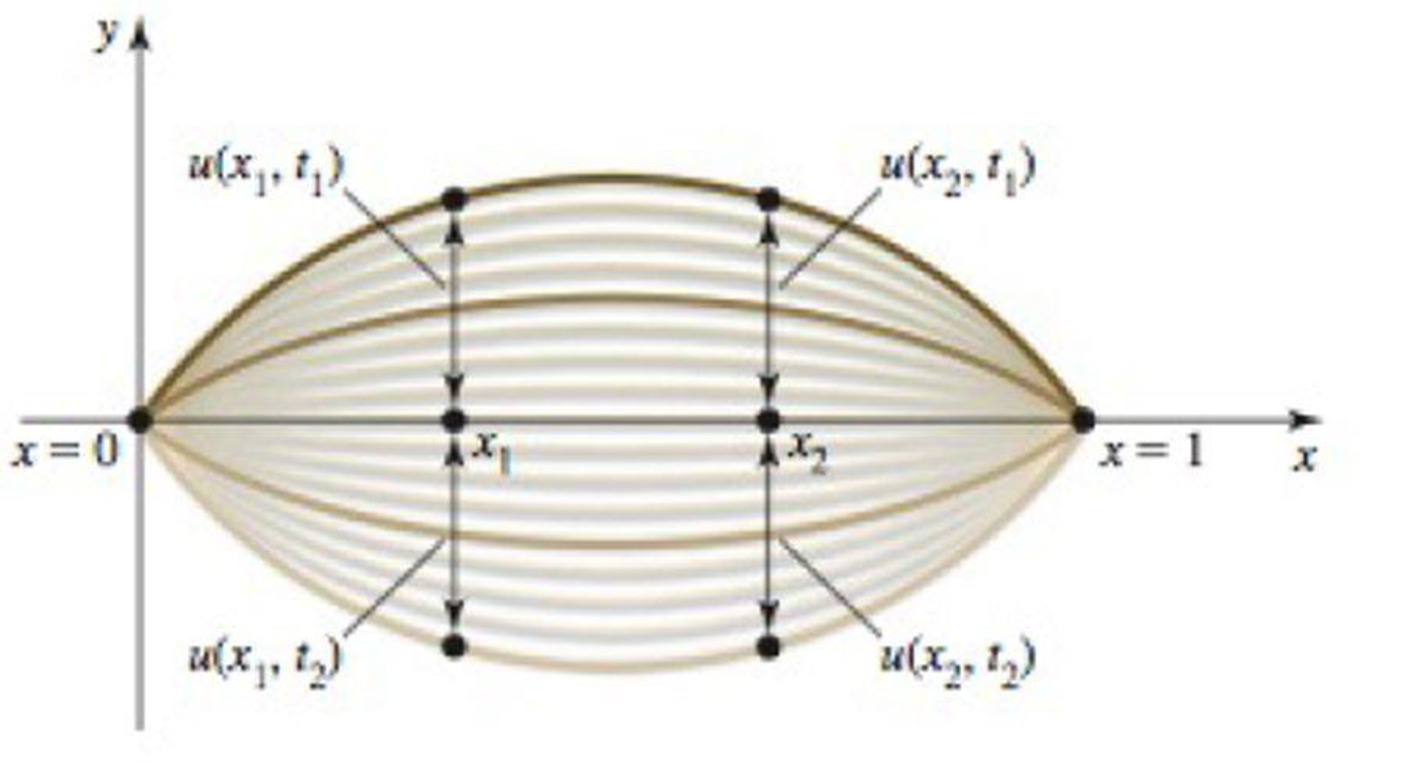
Wave on a string Imagine a string that is fixed at both ends (for example, a guitar string). When plucked, the string forms a standing wave. The displacement u of the string varies with position x and with time t. Suppose it is given by u = f(x, t) = 2 sin (πx) sin (πt/2), for 0 ≤ x ≤ 1 and t ≥ 0 (see figure). At a fixed point in time, the string forms a wave on [0, 1]. Alternatively, if you focus on a point on the string (fix a value of x), that point oscillates up and down in time.

 a.    What is the period of the motion in time?

 b.    Find the rate of change of the displacement with respect to time at a constant position (which is the vertical velocity of a point on the string).

 c.    At a fixed time, what point on the string is moving fastest?

 d.    At a fixed position on the string, when is the string moving fastest?

 e.    Find the rate of change of the displacement with respect to position at a constant time (which is the slope of the string).

 f.    At a fixed time, where is the slope of the string greatest?

Chapter 15.3, Problem 86E, Wave on a string Imagine a string that is fixed at both ends (for example, a guitar string). When

Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 15.3, Problem 85E
Next
Chapter 15.3, Problem 87E
Students have asked these similar questions
Let a = (-4, 5, 4) and 6 = (1,0, -1). Find the angle between the vector 1) The exact angle is cos 2) The approximation in radians is
Find the (exact) direction cosines and (rounded to 1 decimal place) direction angles of = (3,7,6)
Let a = (-1, -2, -3) and 6 = (-4, 0, 1). Find the component of b onto a.

Chapter 15 Solutions

Calculus Early Transcendentals 3rd.edition I.r.c.

Ch. 15.1 - Find the domains of f(x, y) = sin xy and g(x, y) =...Ch. 15.1 - Does the graph of a hyperboloid of one sheet...Ch. 15.1 - Find a function whose graph is the lower half of...Ch. 15.1 - Can two level curves of a function intersect?...Ch. 15.1 - Prob. 5QCCh. 15.1 - Prob. 6QCCh. 15.1 - Prob. 7QCCh. 15.1 - Prob. 8QCCh. 15.1 - What is the domain of the function w = f(x, y, z)...Ch. 15.1 - What is domain of f(x, y) = x2y xy2?
Ch. 15.1 - What is the domain of g(x, y) = 1/(xy)?Ch. 15.1 - What is the domain of h(x,y)=xy?Ch. 15.1 - How many axes (or how many dimensions) are needed...Ch. 15.1 - Explain how to graph the level curves of a surface...Ch. 15.1 - Given the function f(x, y) = 10x+y, evaluate f(2,...Ch. 15.1 - Prob. 8ECh. 15.1 - The function z = f(x, y) gives the elevation z (in...Ch. 15.1 - The function z = f(x, y) gives the elevation z (in...Ch. 15.1 - Describe in words the level curves of the...Ch. 15.1 - How many axes (or how many dimensions) are needed...Ch. 15.1 - The domain of Q = f(u, v, w, x, y, z) lies in n...Ch. 15.1 - Give two methods for graphically representing a...Ch. 15.1 - Domains Find the domain of the following...Ch. 15.1 - Prob. 16ECh. 15.1 - Domains Find the domain of the following...Ch. 15.1 - Domains Find the domain of the following...Ch. 15.1 - Domains Find the domain of the following...Ch. 15.1 - Domains Find the domain of the following...Ch. 15.1 - Domains Find the domain of the following...Ch. 15.1 - Domains Find the domain of the following...Ch. 15.1 - Domains Find the domain of the following...Ch. 15.1 - Domains Find the domain of the following...Ch. 15.1 - Graphs of familiar functions Use what you learned...Ch. 15.1 - Graphs of familiar functions Use what you learned...Ch. 15.1 - Graphs of familiar functions Use what you learned...Ch. 15.1 - Graphs of familiar functions Use what you learned...Ch. 15.1 - Graphs of familiar functions Use what you learned...Ch. 15.1 - Graphs of familiar functions Use what you learned...Ch. 15.1 - Graphs of familiar functions Use what you learned...Ch. 15.1 - Graphs of familiar functions Use what you learned...Ch. 15.1 - Graphs of familiar functions Use what you learned...Ch. 15.1 - Matching level curves with surfaces Match surfaces...Ch. 15.1 - Matching surfaces Match functions ad with surfaces...Ch. 15.1 - Level curves Graph several level curves of the...Ch. 15.1 - Level curves Graph several level curves of the...Ch. 15.1 - Level curves Graph several level curves of the...Ch. 15.1 - Level curves Graph several level curves of the...Ch. 15.1 - Level curves Graph several level curves of the...Ch. 15.1 - Level curves Graph several level curves of the...Ch. 15.1 - Level curves Graph several level curves of the...Ch. 15.1 - Level curves Graph several level curves of the...Ch. 15.1 - Earned run average A baseball pitchers earned run...Ch. 15.1 - Electric potential function The electric potential...Ch. 15.1 - Cobb-Douglas production function The output Q of...Ch. 15.1 - Resistors in parallel Two resistors wired in...Ch. 15.1 - Level curves of a savings account Suppose you make...Ch. 15.1 - Level curves of a savings plan Suppose you make...Ch. 15.1 - Domains of functions of three or more variables...Ch. 15.1 - Domains of functions of three or more variables...Ch. 15.1 - Domains of functions of three or more variables...Ch. 15.1 - Domains of functions of three or more variables...Ch. 15.1 - Domains of functions of three or more variables...Ch. 15.1 - Domains of functions of three or more variables...Ch. 15.1 - Prob. 56ECh. 15.1 - Explain why or why not Determine whether the...Ch. 15.1 - Quarterback passer ratings One measurement of the...Ch. 15.1 - Ideal Gas Law Many gases can be modeled by the...Ch. 15.1 - Water waves A snapshot of a water wave moving...Ch. 15.1 - Approximate mountains Suppose the elevation of...Ch. 15.1 - Graphing functions a.Determine the domain and...Ch. 15.1 - Prob. 63ECh. 15.1 - Prob. 64ECh. 15.1 - Graphing functions a.Determine the domain and...Ch. 15.1 - Graphing functions a.Determine the domain and...Ch. 15.1 - Prob. 67ECh. 15.1 - Prob. 68ECh. 15.1 - Prob. 69ECh. 15.1 - Prob. 70ECh. 15.1 - Peaks and valleys The following functions have...Ch. 15.1 - Prob. 72ECh. 15.1 - Prob. 73ECh. 15.1 - Level surfaces Find an equation for the family of...Ch. 15.1 - Level surfaces Find an equation for the family of...Ch. 15.1 - Level surfaces Find an equation for the family of...Ch. 15.1 - Level surfaces Find an equation for the family of...Ch. 15.1 - Prob. 78ECh. 15.1 - Challenge domains Find the domains of the...Ch. 15.1 - Prob. 80ECh. 15.1 - Prob. 81ECh. 15.1 - Prob. 82ECh. 15.2 - Which of the following limits exist? Ch. 15.2 - Give an example of a set that contains none of its...Ch. 15.2 - Can the limit be evaluated by direct...Ch. 15.2 - What is the analog of the Two-Path Test for...Ch. 15.2 - Prob. 5QCCh. 15.2 - Prob. 1ECh. 15.2 - Explain why f(x, y) must approach a unique number...Ch. 15.2 - What does it mean to say that limits of...Ch. 15.2 - Suppose (a, b) is on the boundary of the domain of...Ch. 15.2 - Explain how examining limits along multiple paths...Ch. 15.2 - Explain why evaluating a limit along a finite...Ch. 15.2 - What three conditions must be met for a function f...Ch. 15.2 - Let R be the unit disk {(x, y): x2 + y2 1} with...Ch. 15.2 - At what points of 2 is a rational function of two...Ch. 15.2 - Prob. 10ECh. 15.2 - Evaluate lim(x,y)(5,5)x2y2x+yCh. 15.2 - Let f(x)=x22xy2+1x22xy2+1 Use the Two-Path Test to...Ch. 15.2 - Limits of functions Evaluate the following limits....Ch. 15.2 - Limits of functions Evaluate the following limits....Ch. 15.2 - Limits of functions Evaluate the following limits....Ch. 15.2 - Limits of functions Evaluate the following limits....Ch. 15.2 - Limits of functions Evaluate the following limits....Ch. 15.2 - Limits of functions Evaluate the following limits....Ch. 15.2 - Limits of functions Evaluate the following limits....Ch. 15.2 - Limits of functions Evaluate the following limits....Ch. 15.2 - Prob. 21ECh. 15.2 - Limits at boundary points Evaluate the following...Ch. 15.2 - Limits at boundary points Evaluate the following...Ch. 15.2 - Limits at boundary points Evaluate the following...Ch. 15.2 - Limits at boundary points Evaluate the following...Ch. 15.2 - Prob. 26ECh. 15.2 - Limits at boundary points Evaluate the following...Ch. 15.2 - Prob. 28ECh. 15.2 - Prob. 29ECh. 15.2 - Prob. 30ECh. 15.2 - Nonexistence of limits Use the Two-Path Test to...Ch. 15.2 - Prob. 32ECh. 15.2 - Nonexistence of limits Use the Two-Path Test to...Ch. 15.2 - Nonexistence of limits Use the Two-Path Test to...Ch. 15.2 - Continuity At what points of 2 are the following...Ch. 15.2 - Continuity At what points of 2 are the following...Ch. 15.2 - Continuity At what points of 2 are the following...Ch. 15.2 - Continuity At what points of 2 are the following...Ch. 15.2 - Continuity At what points of 2 are the following...Ch. 15.2 - Continuity At what points of 2 are the following...Ch. 15.2 - Continuity At what points of 2 are the following...Ch. 15.2 - Continuity At what points of 2 are the following...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Continuity of composite functions At what points...Ch. 15.2 - Limits of functions of three variables Evaluate...Ch. 15.2 - Limits of functions of three variables Evaluate...Ch. 15.2 - Limits of functions of three variables Evaluate...Ch. 15.2 - Limits of functions of three variables Evaluate...Ch. 15.2 - Limits of functions of three variables Evaluate...Ch. 15.2 - Limits of functions of three variables Evaluate...Ch. 15.2 - Prob. 61ECh. 15.2 - Miscellaneous limits Use the method of your choice...Ch. 15.2 - Miscellaneous limits Use the method of your choice...Ch. 15.2 - Miscellaneous limits Use the method of your choice...Ch. 15.2 - Prob. 65ECh. 15.2 - Miscellaneous limits Use the method of your choice...Ch. 15.2 - Miscellaneous limits Use the method of your choice...Ch. 15.2 - Prob. 68ECh. 15.2 - Miscellaneous limits Use the method of your choice...Ch. 15.2 - Prob. 70ECh. 15.2 - Limits of composite functions Evaluate the...Ch. 15.2 - Limits of composite functions Evaluate the...Ch. 15.2 - Limits of composite functions Evaluate the...Ch. 15.2 - Prob. 74ECh. 15.2 - Prob. 75ECh. 15.2 - Prob. 76ECh. 15.2 - Piecewise function Let...Ch. 15.2 - Prob. 78ECh. 15.2 - Prob. 79ECh. 15.2 - Prob. 80ECh. 15.2 - Prob. 81ECh. 15.2 - Prob. 82ECh. 15.2 - Nonexistence of limits Show that...Ch. 15.2 - Prob. 84ECh. 15.2 - Prob. 85ECh. 15.2 - Limit proof Use the formal definition of a limit...Ch. 15.2 - Limit proof Use the formal definition of a limit...Ch. 15.2 - Proof of Limit Law 1 Use the formal definition of...Ch. 15.2 - Proof of Limit Law 3 Use the formal definition of...Ch. 15.3 - Compute fx and fy for f(x, y) = 2xy.Ch. 15.3 - Which of the following expressions are equivalent...Ch. 15.3 - Compute fxxx and f xxy for f(x, y) = x3y.Ch. 15.3 - Compute fxz and fzz for f(x, y, z) = xyz x2z +...Ch. 15.3 - Explain why, in Figure 15.33, the slopes of the...Ch. 15.3 - Suppose you are standing on the surface z = f(x,...Ch. 15.3 - Prob. 2ECh. 15.3 - Prob. 3ECh. 15.3 - Find fx and fy when f(x, y) = y8 + 2x6 + 2xy.Ch. 15.3 - Find fx and fy when f(x, y) = 3x2y + 2.Ch. 15.3 - Prob. 6ECh. 15.3 - Verify that fxy = fyx. for f(x, y) = 2x3 + 3y2 +...Ch. 15.3 - Verify that fxy = fyx, for f(x, y) = xey.Ch. 15.3 - Find fx,, fy, and fz, for f(x, y, z) = xy + xz +...Ch. 15.3 - The volume of a right circular cylinder with...Ch. 15.3 - Prob. 11ECh. 15.3 - Prob. 12ECh. 15.3 - Prob. 13ECh. 15.3 - Prob. 14ECh. 15.3 - Prob. 15ECh. 15.3 - Prob. 16ECh. 15.3 - Prob. 17ECh. 15.3 - Prob. 18ECh. 15.3 - Prob. 19ECh. 15.3 - Prob. 20ECh. 15.3 - Prob. 21ECh. 15.3 - Prob. 22ECh. 15.3 - Prob. 23ECh. 15.3 - Prob. 24ECh. 15.3 - Prob. 25ECh. 15.3 - Prob. 26ECh. 15.3 - Prob. 27ECh. 15.3 - Prob. 28ECh. 15.3 - Prob. 29ECh. 15.3 - Prob. 30ECh. 15.3 - Partial derivatives Find the first partial...Ch. 15.3 - Prob. 32ECh. 15.3 - Prob. 33ECh. 15.3 - Prob. 34ECh. 15.3 - Prob. 35ECh. 15.3 - Miscellaneous partial derivatives Compute the...Ch. 15.3 - Prob. 37ECh. 15.3 - Prob. 38ECh. 15.3 - Prob. 39ECh. 15.3 - Prob. 40ECh. 15.3 - Prob. 41ECh. 15.3 - Prob. 42ECh. 15.3 - Prob. 43ECh. 15.3 - Prob. 44ECh. 15.3 - Prob. 45ECh. 15.3 - Prob. 46ECh. 15.3 - Prob. 47ECh. 15.3 - Prob. 48ECh. 15.3 - Prob. 49ECh. 15.3 - Equality of mixed partial derivatives Verify that...Ch. 15.3 - Prob. 51ECh. 15.3 - Equality of mixed partial derivatives Verify that...Ch. 15.3 - Prob. 53ECh. 15.3 - Prob. 54ECh. 15.3 - Prob. 55ECh. 15.3 - Prob. 56ECh. 15.3 - Prob. 57ECh. 15.3 - Prob. 58ECh. 15.3 - Prob. 59ECh. 15.3 - Prob. 60ECh. 15.3 - Prob. 61ECh. 15.3 - Prob. 62ECh. 15.3 - Prob. 63ECh. 15.3 - Prob. 64ECh. 15.3 - Prob. 65ECh. 15.3 - Prob. 66ECh. 15.3 - Prob. 67ECh. 15.3 - Prob. 68ECh. 15.3 - Gas law calculations Consider the Ideal Gas Law PV...Ch. 15.3 - Body mass index The body mass index (BMI) for an...Ch. 15.3 - Resistors in parallel Two resistors in an...Ch. 15.3 - Spherical caps The volume of the cap of a sphere...Ch. 15.3 - Heat equation The flow of hear along a thin...Ch. 15.3 - Heat equation The flow of hear along a thin...Ch. 15.3 - Heat equation The flow of hear along a thin...Ch. 15.3 - Prob. 76ECh. 15.3 - Nondifferentiability? Consider the following...Ch. 15.3 - Nondifferentiability? Consider the following...Ch. 15.3 - Prob. 79ECh. 15.3 - Prob. 80ECh. 15.3 - Prob. 81ECh. 15.3 - Prob. 82ECh. 15.3 - Electric potential function The electric potential...Ch. 15.3 - Prob. 84ECh. 15.3 - Prob. 85ECh. 15.3 - Wave on a string Imagine a string that is fixed at...Ch. 15.3 - Wave equation Traveling waves (for example, water...Ch. 15.3 - Wave equation Traveling waves (for example, water...Ch. 15.3 - Wave equation Traveling waves (for example, water...Ch. 15.3 - Laplaces equation A classical equation of...Ch. 15.3 - Laplaces equation A classical equation of...Ch. 15.3 - Laplaces equation A classical equation of...Ch. 15.3 - Laplaces equation A classical equation of...Ch. 15.3 - Prob. 94ECh. 15.3 - Differentiability Use the definition of...Ch. 15.3 - Nondifferentiability? Consider the following...Ch. 15.3 - Nondifferentiability? Consider the following...Ch. 15.3 - Prob. 98ECh. 15.3 - Derivatives of an integral Let h be continuous for...Ch. 15.4 - Explain why Theorem 15.7 reduces to the Chain Rule...Ch. 15.4 - Suppose w = f(x, y, z), where x = g(s, t), y =...Ch. 15.4 - If Q is a function of w, x, y, and z, each of...Ch. 15.4 - Use the method of Example 5 to find dy/dx when...Ch. 15.4 - Suppose z = f(x, y), where x and y are functions...Ch. 15.4 - Let z be a function of x and y, while x and y are...Ch. 15.4 - Suppose w is a function of x, y and z, which are...Ch. 15.4 - Let z = f(x, y), x = g(s, t), and y = h(s, t)....Ch. 15.4 - Given that w = F(x, y, z), and x, y, and z are...Ch. 15.4 - Suppose F(x, y) = 0 and y is a differentiable...Ch. 15.4 - Evaluate dz/dt, where z = x2+y3, x = t2 and y = t,...Ch. 15.4 - Prob. 8ECh. 15.4 - Chain Rule with one independent variable Use...Ch. 15.4 - Chain Rule with one independent variable Use...Ch. 15.4 - Chain Rule with one independent variable Use...Ch. 15.4 - Chain Rule with one independent variable Use...Ch. 15.4 - Chain Rule with one independent variable Use...Ch. 15.4 - Chain Rule with one independent variable Use...Ch. 15.4 - Chain Rule with one independent variable Use...Ch. 15.4 - Chain Rule with one independent variable Use...Ch. 15.4 - Chain Rule with one independent variable Use...Ch. 15.4 - Chain Rule with one independent variable Use...Ch. 15.4 - Chain Rule with several independent variables Find...Ch. 15.4 - Chain Rule with several independent variables Find...Ch. 15.4 - Chain Rule with several independent variables Find...Ch. 15.4 - Chain Rule with several independent variables Find...Ch. 15.4 - Chain Rule with several independent variables Find...Ch. 15.4 - Prob. 24ECh. 15.4 - Chain Rule with several independent variables Find...Ch. 15.4 - Prob. 26ECh. 15.4 - Changing cylinder The volume of a right circular...Ch. 15.4 - Changing pyramid The volume of a pyramid with a...Ch. 15.4 - Derivative practice two ways Find the indicated...Ch. 15.4 - Derivative practice two ways Find the indicated...Ch. 15.4 - Making trees Use a tree diagram to write the...Ch. 15.4 - Prob. 32ECh. 15.4 - Prob. 33ECh. 15.4 - Prob. 34ECh. 15.4 - Implicit differentiation Given the following...Ch. 15.4 - Implicit differentiation Given the following...Ch. 15.4 - Implicit differentiation Given the following...Ch. 15.4 - Implicit differentiation Given the following...Ch. 15.4 - Implicit differentiation Given the following...Ch. 15.4 - Implicit differentiation Given the following...Ch. 15.4 - Prob. 41ECh. 15.4 - Prob. 42ECh. 15.4 - Prob. 43ECh. 15.4 - Prob. 44ECh. 15.4 - Prob. 45ECh. 15.4 - Prob. 46ECh. 15.4 - Prob. 47ECh. 15.4 - Prob. 48ECh. 15.4 - Prob. 49ECh. 15.4 - Derivative practice Find the indicated derivative...Ch. 15.4 - Derivative practice Find the indicated derivative...Ch. 15.4 - Derivative practice Find the indicated derivative...Ch. 15.4 - Derivative practice Find the indicated derivative...Ch. 15.4 - Prob. 54ECh. 15.4 - Change on a line Suppose w=(x,y,z) and is the line...Ch. 15.4 - Prob. 56ECh. 15.4 - Implicit differentiation with three variables Use...Ch. 15.4 - Prob. 58ECh. 15.4 - Prob. 59ECh. 15.4 - More than one way Let exyz = 2. Find zx and zy in...Ch. 15.4 - Walking on a surface Consider the following...Ch. 15.4 - Walking on a surface Consider the following...Ch. 15.4 - Walking on a surface Consider the following...Ch. 15.4 - Walking on a surface Consider the following...Ch. 15.4 - Conservation of energy A projectile with mass m is...Ch. 15.4 - Utility functions in economics Economists use...Ch. 15.4 - Constant volume tori The volume of a solid torus...Ch. 15.4 - Body surface area One of several empirical...Ch. 15.4 - The Ideal Gas Law The pressure, temperature, and...Ch. 15.4 - Prob. 70ECh. 15.4 - Prob. 71ECh. 15.4 - Change of coordinates Recall that Cartesian and...Ch. 15.4 - Change of coordinates continued An important...Ch. 15.4 - Prob. 75ECh. 15.4 - Prob. 76ECh. 15.4 - Prob. 77ECh. 15.5 - Explain Why, when u = 1, 0 in the definition of...Ch. 15.5 - In the parametric description x = a + su1 and y =...Ch. 15.5 - In Example 1, evaluate Du f(3, 2) and Dv f(3, 2)....Ch. 15.5 - Draw a circle in the xy-plane centered at the...Ch. 15.5 - Prob. 5QCCh. 15.5 - Prob. 6QCCh. 15.5 - Prob. 1ECh. 15.5 - How do you compute the gradient of the functions...Ch. 15.5 - Prob. 3ECh. 15.5 - Prob. 4ECh. 15.5 - Given a function f, explain the relationship...Ch. 15.5 - The level curves of the surface z=x2+y2 are...Ch. 15.5 - Suppose f is differentiable at (3, 4), f(3, 4) =...Ch. 15.5 - Suppose f is differentiable at (9, 9), f(9, 9) =...Ch. 15.5 - Suppose f is differentiable at (3, 4). Assume u,...Ch. 15.5 - Suppose f is differentiable at (1, 2) and ∇ f(1,...Ch. 15.5 - Directional derivatives Consider the function...Ch. 15.5 - Directional derivatives Consider the function...Ch. 15.5 - Computing gradients Compute the gradient of the...Ch. 15.5 - Computing gradients Compute the gradient of the...Ch. 15.5 - Computing gradients Compute the gradient of the...Ch. 15.5 - Computing gradients Compute the gradient of the...Ch. 15.5 - Computing gradients Compute the gradient of the...Ch. 15.5 - Computing gradients Compute the gradient of the...Ch. 15.5 - Computing gradients Compute the gradient of the...Ch. 15.5 - Computing gradients Compute the gradient of the...Ch. 15.5 - Computing directional derivatives with the...Ch. 15.5 - Computing directional derivatives with the...Ch. 15.5 - Prob. 23ECh. 15.5 - Computing directional derivatives with the...Ch. 15.5 - Computing directional derivatives with the...Ch. 15.5 - Prob. 26ECh. 15.5 - Computing directional derivatives with the...Ch. 15.5 - Computing directional derivatives with the...Ch. 15.5 - Computing directional derivatives with the...Ch. 15.5 - Computing directional derivatives with the...Ch. 15.5 - Direction of steepest ascent and descent Consider...Ch. 15.5 - Direction of steepest ascent and descent Consider...Ch. 15.5 - Direction of steepest ascent and descent Consider...Ch. 15.5 - Direction of steepest ascent and descent Consider...Ch. 15.5 - Direction of steepest ascent and descent Consider...Ch. 15.5 - Direction of steepest ascent and descent Consider...Ch. 15.5 - Interpreting directional derivatives A function f...Ch. 15.5 - Interpreting directional derivatives A function f...Ch. 15.5 - Interpreting directional derivatives A function f...Ch. 15.5 - Interpreting directional derivatives A function f...Ch. 15.5 - Interpreting directional derivatives A function f...Ch. 15.5 - Interpreting directional derivatives A function f...Ch. 15.5 - Directions of change Consider the following...Ch. 15.5 - Prob. 44ECh. 15.5 - Prob. 45ECh. 15.5 - 43-46. Directions of change Consider the following...Ch. 15.5 - Level curves Consider the paraboloid f(x, y) = 16 ...Ch. 15.5 - Level curves Consider the paraboloid f(x, y) = 16 ...Ch. 15.5 - Level curves Consider the paraboloid f(x, y) = 16 ...Ch. 15.5 - Level curves Consider the paraboloid f(x, y) = 16 ...Ch. 15.5 - Level curves Consider the upper half of the...Ch. 15.5 - Level curves Consider the upper half of the...Ch. 15.5 - Level curves Consider the upper half of the...Ch. 15.5 - Prob. 54ECh. 15.5 - Path of steepest descent Consider each of the...Ch. 15.5 - Path of steepest descent Consider each of the...Ch. 15.5 - Path of steepest descent Consider each of the...Ch. 15.5 - Path of steepest descent Consider each of the...Ch. 15.5 - Gradients in three dimensions Consider the...Ch. 15.5 - Gradients in three dimensions Consider the...Ch. 15.5 - Gradients in three dimensions Consider the...Ch. 15.5 - Gradients in three dimensions Consider the...Ch. 15.5 - Gradients in three dimensions Consider the...Ch. 15.5 - Gradients in three dimensions Consider the...Ch. 15.5 - Gradients in three dimensions Consider the...Ch. 15.5 - Gradients in three dimensions Consider the...Ch. 15.5 - Explain why or why not Determine whether the...Ch. 15.5 - Gradient of a composite function Consider the...Ch. 15.5 - Directions of zero change Find the directions in...Ch. 15.5 - Prob. 70ECh. 15.5 - Directions of zero change Find the directions in...Ch. 15.5 - Directions of zero change Find the directions in...Ch. 15.5 - Steepest ascent on a plane Suppose a long sloping...Ch. 15.5 - Gradient of a distance function Let (a, b) be a...Ch. 15.5 - Looking aheadtangent planes Consider the following...Ch. 15.5 - Prob. 76ECh. 15.5 - Looking aheadtangent planes Consider the following...Ch. 15.5 - Prob. 78ECh. 15.5 - Prob. 79ECh. 15.5 - Prob. 80ECh. 15.5 - Potential functions Potential functions arise...Ch. 15.5 - Potential functions Potential functions arise...Ch. 15.5 - Prob. 83ECh. 15.5 - Prob. 84ECh. 15.5 - Rules for gradients Use the definition of the...Ch. 15.5 - Prob. 86ECh. 15.5 - Prob. 87ECh. 15.5 - Prob. 88ECh. 15.5 - Using gradient rules Use the gradient rules of...Ch. 15.5 - Using gradient rules Use the gradient rules of...Ch. 15.5 - Prob. 91ECh. 15.6 - Write the function z = xy + x y in the form F(x,...Ch. 15.6 - Prob. 2QCCh. 15.6 - Prob. 3QCCh. 15.6 - Prob. 4QCCh. 15.6 - Suppose n is a vector normal to the tangent plane...Ch. 15.6 - Write the explicit function z = xy2 + x2y 10 in...Ch. 15.6 - Write an equation for the plane tangent to the...Ch. 15.6 - Prob. 4ECh. 15.6 - Explain how to approximate a function f at a point...Ch. 15.6 - Explain how to approximate the change in a...Ch. 15.6 - Write the approximate change formula for a...Ch. 15.6 - Write the differential dw for the function w =...Ch. 15.6 - Suppose f(1, 2) = 4, fx(1, 2) = 5, and fy(1, 2) =...Ch. 15.6 - Suppose f(l, 2) = 4, fx(1, 2) = 5, and fy(1, 2) =...Ch. 15.6 - Suppose F(0, 2, 1) = 0, Fx(0, 2, 1) = 3, Fy(0, 2,...Ch. 15.6 - Suppose F(0, 2, 1) = 0, Fx(0, 2, 1) = 3, Fy(0, 2,...Ch. 15.6 - Tangent planes for F(x,y,z) = 0 Find an equation...Ch. 15.6 - Tangent planes for F(x,y,z) = 0 Find an equation...Ch. 15.6 - Tangent planes for F(x,y,z) = 0 Find an equation...Ch. 15.6 - Tangent planes for F(x,y,z) = 0 Find an equation...Ch. 15.6 - Tangent planes for z = f (x, y) Find an equation...Ch. 15.6 - Tangent planes for z = f (x, y) Find an equation...Ch. 15.6 - Tangent planes for z = f (x, y) Find an equation...Ch. 15.6 - Tangent planes for z = f (x, y) Find an equation...Ch. 15.6 - Tangent planes for F(x,y,z) = 0 Find an equation...Ch. 15.6 - Tangent planes for F(x, y, z) = 0 Find an equation...Ch. 15.6 - Tangent planes for F(x, y, z) = 0 Find an equation...Ch. 15.6 - Tangent planes for F(x, y, z) = 0 Find an equation...Ch. 15.6 - Tangent planes for z = f (x, y) Find an equation...Ch. 15.6 - Prob. 26ECh. 15.6 - Tangent planes for z = f (x, y) Find an equation...Ch. 15.6 - Tangent planes for z = f (x, y) Find an equation...Ch. 15.6 - Tangent planes Find an equation of the plane...Ch. 15.6 - Tangent planes Find an equation of the plane...Ch. 15.6 - Tangent planes Find an equation of the plane...Ch. 15.6 - Tangent planes Find an equation of the plane...Ch. 15.6 - Linear approximation a.Find the linear...Ch. 15.6 - Linear approximation a.Find the linear...Ch. 15.6 - Linear approximation a.Find the linear...Ch. 15.6 - Linear approximation a.Find the linear...Ch. 15.6 - Linear Approximation a. Find the linear...Ch. 15.6 - Linear Approximation a. Find the linear...Ch. 15.6 - Approximate function change Use differentials to...Ch. 15.6 - Approximate function change Use differentials to...Ch. 15.6 - Approximate function change Use differentials to...Ch. 15.6 - Approximate function change Use differentials to...Ch. 15.6 - Changes in torus surface area The surface area of...Ch. 15.6 - Changes in cone volume The volume of a right...Ch. 15.6 - Area of an ellipse The area of an ellipse with...Ch. 15.6 - Volume of a paraboloid The volume of a segment of...Ch. 15.6 - Differentials with more than two variables Write...Ch. 15.6 - Differentials with more than two variables Write...Ch. 15.6 - Differentials with more than two variables Write...Ch. 15.6 - Differentials with more than two variables Write...Ch. 15.6 - Law of Cosines The side lengths of any triangle...Ch. 15.6 - Explain why or why not Determine whether the...Ch. 15.6 - Horizontal tangent planes Find the points at which...Ch. 15.6 - Horizontal tangent planes Find the points at which...Ch. 15.6 - Horizontal tangent planes Find the points at which...Ch. 15.6 - Horizontal tangent planes Find the points at which...Ch. 15.6 - Prob. 58ECh. 15.6 - Surface area of a cone A cone with height h and...Ch. 15.6 - Line tangent to an intersection curve Consider the...Ch. 15.6 - Water-level changes A conical tank with radius...Ch. 15.6 - Prob. 63ECh. 15.6 - Floating-point operations In general, real numbers...Ch. 15.6 - Probability of at least one encounter Suppose that...Ch. 15.6 - Two electrical resistors When two electrical...Ch. 15.6 - Three electrical resistors Extending Exercise 66,...Ch. 15.6 - Prob. 68ECh. 15.6 - Logarithmic differentials Let f be a...Ch. 15.7 - The parabola z = x2 + y2 4x + 2y + 5 has a local...Ch. 15.7 - Consider the plane tangent to a surface at a...Ch. 15.7 - Compute the discriminant D(x, y) of f(x, y) =...Ch. 15.7 - Does the linear function f(x, y) = 2x + 3y have an...Ch. 15.7 - Describe the appearance of a smooth surface with a...Ch. 15.7 - Describe the usual appearance of a smooth surface...Ch. 15.7 - What are the conditions for a critical point of a...Ch. 15.7 - If fx (a, b) = fy (a, b) = 0, does it follow the f...Ch. 15.7 - Consider the function z = f(x, y). What is the...Ch. 15.7 - Prob. 6ECh. 15.7 - What is an absolute minimum value of a function f...Ch. 15.7 - What is the procedure for locating absolute...Ch. 15.7 - Assume the second derivatives of fare continuous...Ch. 15.7 - Assume the second derivatives of fare continuous...Ch. 15.7 - Assume the second derivatives of fare continuous...Ch. 15.7 - Assume the second derivatives of fare continuous...Ch. 15.7 - Critical points Find all critical points of the...Ch. 15.7 - Critical points Find all critical points of the...Ch. 15.7 - Critical points Find all critical points of the...Ch. 15.7 - Critical points Find all critical points of the...Ch. 15.7 - Critical points Find all critical points of the...Ch. 15.7 - Critical points Find all critical points of the...Ch. 15.7 - Critical points Find all critical points of the...Ch. 15.7 - Critical points Find all critical points of the...Ch. 15.7 - Critical points Find all critical points of the...Ch. 15.7 - Critical points Find all critical points of the...Ch. 15.7 - Prob. 23ECh. 15.7 - Prob. 24ECh. 15.7 - Prob. 25ECh. 15.7 - Prob. 26ECh. 15.7 - Prob. 27ECh. 15.7 - Prob. 28ECh. 15.7 - Analyzing critical points Find the critical points...Ch. 15.7 - Prob. 30ECh. 15.7 - Analyzing critical points Find the critical points...Ch. 15.7 - Analyzing critical points Find the critical points...Ch. 15.7 - Prob. 33ECh. 15.7 - Prob. 34ECh. 15.7 - Analyzing critical points Find the critical points...Ch. 15.7 - Analyzing critical points Find the critical points...Ch. 15.7 - Prob. 37ECh. 15.7 - Prob. 38ECh. 15.7 - Analyzing critical points Find the critical points...Ch. 15.7 - Prob. 40ECh. 15.7 - Inconclusive tests Show that the Second Derivative...Ch. 15.7 - Inconclusive tests Show that the Second Derivative...Ch. 15.7 - Shipping regulations A shipping company handles...Ch. 15.7 - Cardboard boxes A lidless box is to be made using...Ch. 15.7 - Cardboard boxes A lidless cardboard box is to be...Ch. 15.7 - Optimal box Find the dimensions of the largest...Ch. 15.7 - Absolute maxima and minima Find the absolute...Ch. 15.7 - Absolute maxima and minima Find the absolute...Ch. 15.7 - Absolute maxima and minima Find the absolute...Ch. 15.7 - Absolute maxima and minima Find the absolute...Ch. 15.7 - Absolute maxima and minima Find the absolute...Ch. 15.7 - Absolute maxima and minima Find the absolute...Ch. 15.7 - Absolute maxima and minima Find the absolute...Ch. 15.7 - Absolute maxima and minima Find the absolute...Ch. 15.7 - Prob. 55ECh. 15.7 - Absolute maxima and minima Find the absolute...Ch. 15.7 - Pectin Extraction An increase in world production...Ch. 15.7 - Absolute extrema on open and / or unbounded...Ch. 15.7 - Absolute extrema on open and / or unbounded...Ch. 15.7 - Absolute extrema on open and / or unbounded...Ch. 15.7 - Absolute extrema on open and / or unbounded...Ch. 15.7 - Absolute extrema on open and/or unbounded regions...Ch. 15.7 - Lease distance What point on the plane x y + z =...Ch. 15.7 - Absolute extrema on open and/or unbounded regions...Ch. 15.7 - Absolute extrema on open and/or unbounded regions...Ch. 15.7 - Absolute extrema on open and / or unbounded...Ch. 15.7 - Explain why or why not Determine whether the...Ch. 15.7 - Prob. 68ECh. 15.7 - Extreme points from contour plots Based on the...Ch. 15.7 - Optimal box Find the dimensions of the rectangular...Ch. 15.7 - Magic triples Let x, y, and z be nonnegative...Ch. 15.7 - Maximum/minimum of linear functions Let R be a...Ch. 15.7 - Prob. 73ECh. 15.7 - Least squares approximation In its many guises,...Ch. 15.7 - Least squares approximation In its many guises,...Ch. 15.7 - Prob. 76ECh. 15.7 - Prob. 77ECh. 15.7 - Second Derivative Test Suppose the conditions of...Ch. 15.7 - Maximum area triangle Among all triangles with a...Ch. 15.7 - Slicing plane Find an equation of the plane...Ch. 15.7 - Solitary critical points A function of one...Ch. 15.7 - Two mountains without a saddle Show that the...Ch. 15.7 - Powers and roots Assume that x + y + z = 1 with x ...Ch. 15.7 - Ellipsoid inside a tetrahedron (1946 Putnam Exam)...Ch. 15.8 - It can be shown that the function f(x, y) = x2 +...Ch. 15.8 - Prob. 2QCCh. 15.8 - Prob. 3QCCh. 15.8 - In Figure 15.85, explain why, if you move away...Ch. 15.8 - Explain why, at a point that maximizes or...Ch. 15.8 - Describe the steps used to find the absolute...Ch. 15.8 - Prob. 3ECh. 15.8 - Prob. 4ECh. 15.8 - Graphical Lagrange multipliers The following...Ch. 15.8 - Graphical Lagrange multipliers The following...Ch. 15.8 - Lagrange multipliers in two variables Use Lagrange...Ch. 15.8 - Lagrange multipliers in two variables Use Lagrange...Ch. 15.8 - Lagrange multipliers in two variables Use Lagrange...Ch. 15.8 - Lagrange multipliers in two variables Use Lagrange...Ch. 15.8 - Lagrange multipliers in two variables Use Lagrange...Ch. 15.8 - Lagrange multipliers in two variables Use Lagrange...Ch. 15.8 - Lagrange multipliers Each function f has an...Ch. 15.8 - Lagrange multipliers Each function f has an...Ch. 15.8 - Lagrange multipliers Each function f has an...Ch. 15.8 - Lagrange multipliers Each function f has an...Ch. 15.8 - Lagrange multipliers in three variables Use...Ch. 15.8 - Lagrange multipliers in three variables Use...Ch. 15.8 - Lagrange multipliers in three variables Use...Ch. 15.8 - Lagrange multipliers in three variables Use...Ch. 15.8 - Lagrange multipliers Each function f has an...Ch. 15.8 - Lagrange multipliers in three variables Use...Ch. 15.8 - Lagrange multipliers in three variables Use...Ch. 15.8 - Lagrange multipliers Each function f has an...Ch. 15.8 - Lagrange multipliers Each function f has an...Ch. 15.8 - Lagrange multipliers in three variables Use...Ch. 15.8 - Applications of Lagrange multipliers Use Lagrange...Ch. 15.8 - Prob. 28ECh. 15.8 - Prob. 29ECh. 15.8 - Prob. 30ECh. 15.8 - Prob. 31ECh. 15.8 - Prob. 32ECh. 15.8 - Prob. 33ECh. 15.8 - Prob. 34ECh. 15.8 - Prob. 35ECh. 15.8 - Applications of Lagrange multipliers Use Lagrange...Ch. 15.8 - Maximizing utility functions Find the values of l...Ch. 15.8 - Maximizing utility functions Find the values of l...Ch. 15.8 - Maximizing utility functions Find the values of l...Ch. 15.8 - Maximizing utility functions Find the values of l...Ch. 15.8 - Explain why or why not Determine whether the...Ch. 15.8 - Prob. 42ECh. 15.8 - Alternative method Solve the following problem...Ch. 15.8 - Prob. 44ECh. 15.8 - Prob. 45ECh. 15.8 - Prob. 46ECh. 15.8 - Alternative method Solve the following problems...Ch. 15.8 - Prob. 48ECh. 15.8 - Absolute maximum and minimum values Find the...Ch. 15.8 - Prob. 50ECh. 15.8 - Absolute maximum and minimum values Find the...Ch. 15.8 - Extreme points on flattened spheres The equation...Ch. 15.8 - Production functions Economists model the output...Ch. 15.8 - Production functions Economists model the output...Ch. 15.8 - Production functions Economists model the output...Ch. 15.8 - Temperature of an elliptical plate The temperature...Ch. 15.8 - Maximizing a sum 57.Find the maximum value of x1 +...Ch. 15.8 - Prob. 58ECh. 15.8 - Prob. 59ECh. 15.8 - Geometric and arithmetic means Given positive...Ch. 15.8 - Problems with two constraints Given a...Ch. 15.8 - Prob. 62ECh. 15.8 - Two-constraint problems Use the result of Exercise...Ch. 15.8 - Two-constraint problems Use the result of Exercise...Ch. 15.8 - Check assumptions Consider the function f(x, y) =...Ch. 15 - Prob. 1RECh. 15 - Prob. 2RECh. 15 - Prob. 3RECh. 15 - Prob. 4RECh. 15 - Prob. 5RECh. 15 - Graphs Describe the graph of the following...Ch. 15 - Graphs Describe the graph of the following...Ch. 15 - Level curves Make a sketch of several level curves...Ch. 15 - Level curves Make a sketch of several level curves...Ch. 15 - Matching level curves with surfaces Match level...Ch. 15 - Prob. 11RECh. 15 - Prob. 12RECh. 15 - Prob. 13RECh. 15 - Prob. 14RECh. 15 - Prob. 15RECh. 15 - Prob. 16RECh. 15 - Prob. 17RECh. 15 - Prob. 18RECh. 15 - Prob. 19RECh. 15 - Prob. 20RECh. 15 - Prob. 21RECh. 15 - Prob. 22RECh. 15 - Prob. 23RECh. 15 - Prob. 24RECh. 15 - Prob. 25RECh. 15 - Prob. 26RECh. 15 - Prob. 27RECh. 15 - Prob. 28RECh. 15 - Prob. 29RECh. 15 - Laplaces equation Verify that the following...Ch. 15 - Prob. 31RECh. 15 - Chain Rule Use the Chain Rule to evaluate the...Ch. 15 - Chain Rule Use the Chain Rule to evaluate the...Ch. 15 - Chain Rule Use the Chain Rule to evaluate the...Ch. 15 - Prob. 35RECh. 15 - Implicit differentiation Find dy/dx for the...Ch. 15 - Implicit differentiation Find dy/dx for the...Ch. 15 - Walking on a surface Consider the following...Ch. 15 - Walking on a surface Consider the following...Ch. 15 - Constant volume cones Suppose the radius of a...Ch. 15 - Directional derivatives Consider the function f(x,...Ch. 15 - Computing gradients Compute the gradient of the...Ch. 15 - Computing gradients Compute the gradient of the...Ch. 15 - Computing gradients Compute the gradient of the...Ch. 15 - Computing gradients Compute the gradient of the...Ch. 15 - Computing directional derivatives Compute the...Ch. 15 - Computing directional derivatives Compute the...Ch. 15 - Direction of steepest ascent and descent a.Find...Ch. 15 - Prob. 49RECh. 15 - Level curves Let f(x, y) = 8 2x2 y2. For the...Ch. 15 - Level curves Let f(x, y) = 8 2x2 y2. For the...Ch. 15 - Prob. 52RECh. 15 - Prob. 53RECh. 15 - Tangent planes Find an equation of the plane...Ch. 15 - Tangent planes Find an equation of the plane...Ch. 15 - Prob. 56RECh. 15 - Tangent planes Find an equation of the plane...Ch. 15 - Tangent planes Find an equation of the plane...Ch. 15 - Tangent planes Find an equation of the plane...Ch. 15 - Linear approximation a.Find the linear...Ch. 15 - Linear approximation a.Find the linear...Ch. 15 - Changes in a function Estimate the change in the...Ch. 15 - Volume of a cylinder The volume of a cylinder with...Ch. 15 - Volume of an ellipsoid The volume of an ellipsoid...Ch. 15 - Water-level changes A hemispherical tank with a...Ch. 15 - Prob. 66RECh. 15 - Analyzing critical points Identify the critical...Ch. 15 - Analyzing critical points Identify the critical...Ch. 15 - Analyzing critical points Identify the critical...Ch. 15 - Absolute maxima and minima Find the absolute...Ch. 15 - Absolute maxima and minima Find the absolute...Ch. 15 - Prob. 72RECh. 15 - Absolute maxima and minima Find the absolute...Ch. 15 - Prob. 74RECh. 15 - Lagrange multipliers Use Lagrange multipliers to...Ch. 15 - Prob. 76RECh. 15 - Lagrange multipliers Use Lagrange multipliers to...Ch. 15 - Lagrange multipliers Use Lagrange multipliers to...Ch. 15 - Maximum perimeter rectangle Use Lagrange...Ch. 15 - Minimum surface area cylinder Use Lagrange...Ch. 15 - Minimum distance to a cone Find the point(s) on...Ch. 15 - Prob. 82RECh. 15 - Prob. 83RE

Additional Math Textbook Solutions

Find more solutions based on key concepts
A linear equation is solved by using the intersection of graphs method. Find the solution by interpreting the g...

College Algebra with Modeling & Visualization (5th Edition)

A pair of fair dice is rolled. What is the probability that the second die lands on a higher value than does th...

A First Course in Probability (10th Edition)

Mathematical Connections Explain why 25 cents is one-fourth of a dollar, yet 15 minutes is one-fourth of an hou...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

The given expression

Pre-Algebra Student Edition

Implicit differentiation Carry out the following steps. a. Use implicit differentiation to find dydx. b. Find t...

Calculus: Early Transcendentals (2nd Edition)

The table by using the given graph of h.

Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY