Physics for Scientists and Engineers, Volume 2
10th Edition
ISBN: 9781337553582
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 15.2, Problem 15.3QQ
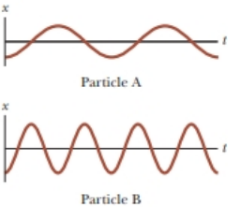
Figure 15.4 shows two curves representing particles undergoing
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
A physical pendulum consists of a disk of radius R = 2 m, whose mass is homogeneously distributed and is
equal to 6 kg, is suspended just at a point on its perimeter. The puck is displaced from its equilibrium position.
until it forms an angle θ = π/16 with respect to the vertical and is then released. find:
a) The period of the system.
b) Make a graph of angular position v/s time where the amplitude, initial phase and
system period.
A particle undergoes a simple harmonic motion with an amplitude A and a total
energy E. When the displacement is one-fourth the amplitude (x A/4), the
ratio of the kinetic energy, K. to the total energy, E, is:
O K/E = 15/16
O K/E= 3/4
O K/E = 1/4
O KE= 8/9
K/E 1/16
KE=1/9
Two blocks, with masses M1 = 2.10 kg and M2 = 9.20 kg, and a spring with spring constant k = 463 N/m are arranged on a horizontal, frictionless surface as shown in the Figure. The coefficient of static friction between the two blocks is 0.540. What is the maximum possible amplitude of the simple harmonic motion if no slippage is to occur between the blocks?
Chapter 15 Solutions
Physics for Scientists and Engineers, Volume 2
Ch. 15.1 - A block on the end of a spring is pulled to...Ch. 15.2 - Consider a graphical representation (Fig. 15.3) of...Ch. 15.2 - Figure 15.4 shows two curves representing...Ch. 15.2 - An object of mass m is hung from a spring and set...Ch. 15.4 - The ball in Figure 15.13 moves in a circle of...Ch. 15.5 - The grandfather clock in the opening storyline...Ch. 15 - A 0.60-kg block attached to a spring with force...Ch. 15 - A piston in a gasoline engine is in simple...Ch. 15 - The position of a particle is given by the...Ch. 15 - A 7.00-kg object is hung from the bottom end of a...
Ch. 15 - Review. A particle moves along the x axis. It is...Ch. 15 - A ball dropped from a height of 4.00 m makes an...Ch. 15 - A particle moving along the x axis in simple...Ch. 15 - The initial position, velocity, and acceleration...Ch. 15 - You attach an object to the bottom end of a...Ch. 15 - To test the resiliency of its bumper during...Ch. 15 - A particle executes simple harmonic motion with an...Ch. 15 - The amplitude of a system moving in simple...Ch. 15 - A simple harmonic oscillator of amplitude A has a...Ch. 15 - Review. A 65.0-kg bungee jumper steps off a bridge...Ch. 15 - Review. A 0.250-kg block resting on a...Ch. 15 - While driving behind a car traveling at 3.00 m/s,...Ch. 15 - A simple pendulum makes 120 complete oscillations...Ch. 15 - A particle of mass m slides without friction...Ch. 15 - A physical pendulum in the form of a planar object...Ch. 15 - A physical pendulum in the form of a planar object...Ch. 15 - Prob. 21PCh. 15 - Consider the physical pendulum of Figure 15.16....Ch. 15 - A watch balance wheel (Fig. P15.25) has a period...Ch. 15 - Show that the time rate of change of mechanical...Ch. 15 - Show that Equation 15.32 is a solution of Equation...Ch. 15 - As you enter a fine restaurant, you realize that...Ch. 15 - A 2.00-kg object attached to a spring moves...Ch. 15 - Considering an undamped, forced oscillator (b =...Ch. 15 - Prob. 29PCh. 15 - Prob. 30PCh. 15 - An object of mass m moves in simple harmonic...Ch. 15 - Review. This problem extends the reasoning of...Ch. 15 - An object attached to a spring vibrates with...Ch. 15 - Review. A rock rests on a concrete sidewalk. An...Ch. 15 - A pendulum of length L and mass M has a spring of...Ch. 15 - To account for the walking speed of a bipedal or...Ch. 15 - Review. A particle of mass 4.00 kg is attached to...Ch. 15 - People who ride motorcycles and bicycles learn to...Ch. 15 - A ball of mass m is connected to two rubber bands...Ch. 15 - Consider the damped oscillator illustrated in...Ch. 15 - Review. A lobstermans buoy is a solid wooden...Ch. 15 - Your thumb squeaks on a plate you have just...Ch. 15 - Prob. 43APCh. 15 - Prob. 44APCh. 15 - A block of mass m is connected to two springs of...Ch. 15 - Review. A light balloon filled with helium of...Ch. 15 - A particle with a mass of 0.500 kg is attached to...Ch. 15 - A smaller disk of radius r and mass m is attached...Ch. 15 - Review. A system consists of a spring with force...Ch. 15 - Review. Why is the following situation impassible?...Ch. 15 - A light, cubical container of volume a3 is...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Why doesnt Earths rotation provide a suitable time standard?
Essential University Physics (3rd Edition)
What is the maximum magnetic intensity in a plane electromagnetic wave whose maximum electric intensity is 100 ...
Introduction To Health Physics
1. What are the temperatures for freezing water on the Celsius and the Fahrenheit scales, respectively? For boi...
Conceptual Physical Science (6th Edition)
Check Your Understanding The changes of momentum for Philae and for Comet 67/P were equal (in magnitude). Were ...
University Physics Volume 1
56. Global Positioning System. Learn more about the global positioning system and its uses. Write a short repo...
The Cosmic Perspective (8th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- C, N A uniform plank of length L and mass M is balanced on a fixed, semicircular bowl of radius R (Fig. P16.19). If the plank is tilted slightly from its equilibrium position and released, will it execute simple harmonic motion? If so, obtain the period of its oscillation.arrow_forwardA simple harmonic oscillator has amplitude A and period T. Find the minimum time required for its position to change from x = A to x = A/2 in terms of the period T.arrow_forwardThe total energy of a simple harmonic oscillator with amplitude 3.00 cm is 0.500 J. a. What is the kinetic energy of the system when the position of the oscillator is 0.750 cm? b. What is the potential energy of the system at this position? c. What is the position for which the potential energy of the system is equal to its kinetic energy? d. For a simple harmonic oscillator, what, if any, are the positions for which the kinetic energy of the system exceeds the maximum potential energy of the system? Explain your answer. FIGURE P16.73arrow_forward
- A particle of mass m moving in one dimension has potential energy U(x) = U0[2(x/a)2 (x/a)4], where U0 and a are positive constants. (a) Find the force F(x), which acts on the particle. (b) Sketch U(x). Find the positions of stable and unstable equilibrium. (c) What is the angular frequency of oscillations about the point of stable equilibrium? (d) What is the minimum speed the particle must have at the origin to escape to infinity? (e) At t = 0 the particle is at the origin and its velocity is positive and equal in magnitude to the escape speed of part (d). Find x(t) and sketch the result.arrow_forwardFigure 12.4 shows two curves representing particles undergoing simple harmonic motion. The correct description of these two motions is that the simple harmonic motion of particle B is (a) of larger angular frequency and larger amplitude than that of particle A, (b) of larger angular frequency and smaller amplitude than that of particle A, (c) of smaller angular frequency and larger amplitude than that of particle A, or (d) of smaller angular frequency and smaller amplitude than that of particle A. Figure 12.4 (Quick Quiz 12.3) Two xt graphs for particles undergoing simple harmonic motion. The amplitudes and frequencies are different for the two particles.arrow_forwardProblem 1: A particle undergoes simple harmonic motion with a frequency of f, = 10 Hz. At t = 0 ; the position of the particle is x(0) = 0.25 m, and the velocity of the particle is v(0) = 0.1 m/s a- Calculate the angular frequency of the oscillation (wo = ??) b- Find the amplitude of the oscillation (A = ??) c- Determine the phase f from the initial conditions (f=??) d- Find the displacement x at any time t. (x(t) = ??)arrow_forward
- Two particles oscillate in simple harmonic motion with amplitude A about the centre of a common straight line of length 2A. Each particle has a period of 1.5 s, and their phase constants differ by 4 rad. (a) How far apart are the particles (in terms of A) 0.5 s after the lagging particle leaves one end of the path? Enter the exact answer in terms of A. ab sin (a) Ωarrow_forwardProvide a detailed explanation please.arrow_forwardA particle undergoes a simple harmonic motion with an amplitude A and a total energy E. When the displacement is one-fourth the amplitude (x = + A/4), the ratio of the kinetic energy, K, to the total energy, E, is: K/E = 8/9 K/E = 1/16 K/E = 1/4 K/E = 1/9 K/E = 15/16 O K/E = 3/4 A block-spring system is in simple harmonic motion on a frictionless horizontalarrow_forward
- the general solution to a harmonic oscillator are related. There are two common forms for the general solution for the position of a harmonic oscillator as a function of time t: 1. x(t) = A cos (wt + p) and 2. x(t) = C cos (wt) + S sin (wt). Either of these equations is a general solution of a second-order differential equation (F= mā); hence both must have at least two--arbitrary constants--parameters that can be adjusted to fit the solution to the particular motion at hand. (Some texts refer to these arbitrary constants as boundary values.) Part D Find analytic expressions for the arbitrary constants A and in Equation 1 (found in Part A) in terms of the constants C and Sin Equation 2 (found in Part B), which are now considered as given parameters. Express the amplitude A and phase (separated by a comma) in terms of C and S. ► View Available Hint(s) Α, φ = V ΑΣΦ ?arrow_forwardA physical pendulum composed of a solid sphere with radius R = 0.500m, is hanged from a ceiling by string of length equal to radius. What are the (a) angular frequency, (b) period, (c) frequency of the system for small angles of oscillation? For solid sphere Icm = 2/5 mr2. Also, why is the distance of the center of mass of the system from the point of oscillation 3R/2?arrow_forwardA 5.0 kg block is attached to a spring of spring constant k=4.00x10^2 N/m and undergoes simple harmonic motion along a frictionless, horizontal tabletop. A second 3.0 kg block sits on top of the first block as shown. The coeffcient of static friction between the two blocks is μs=0.25. What is the greatest amplitude the blocks can undergo without the second block sliding off ? Look at image for refrence. Show all work.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY