
Concept explainers
a.
Find the proportion of homes that have an attached garage.
Check whether people can conclude that more than 60% of the homes have an attached garage.
Find the p-value.
a.
Answer to Problem 62DA
The proportion of homes that have an attached garage is 0.7429.
Yes, people can conclude that more than 60% of the homes have an attached garage.
The p-value is 0.001.
Explanation of Solution
Calculation:
In this case, the test is to check whether more than 60% of the homes have an attached garage.
Let
The proportion of homes that have an attached garage is obtained as follows:
Thus, the proportion of homes that have an attached garage is 0.7429.
The level of significance is 0.05.
Therefore, the value of z score at 0.4500
Decision rule:
Reject the null hypothesis if z > 1.645.
The
Step-by-step procedure to find the test statistic using MINITAB software:
- Choose Stat > Basic Statistics > 1 Proportion.
- Choose Summarized data.
- In Number of events, enter 78. In Number of trials, enter 105.
- Enter Hypothesized proportion as 0.60.
- Check Options, enter Confidence level as 95.0.
- Choose greater than in alternative.
- Select Method as Normal approximation.
- Click OK in all dialogue boxes.
Output is obtained as follows:

Thus, the value of the test statistic is 2.99 and the p-value is 0.001.
In this case, the critical value is 1.645 and the test statistic is 2.99.
Here, the test statistic 2.99 is greater than the critical value 1.645.
That is, 2.99 > 1.645.
Therefore, reject the null hypothesis.
Therefore, people can conclude that more than 60% of the homes have an attached garage.
b.
Find the proportion of homes that have a pool.
Check whether people can conclude that more than 60% of the homes have a pool.
Find the p-value.
b.
Answer to Problem 62DA
The proportion of homes that have an attached garage is 0.6381.
Yes, people can conclude that more than 60% of the homes have a pool.
The p-value is 0.2119.
Explanation of Solution
Calculation:
In this case, the test is to check whether more than 60% of the homes have a pool.
Let
The proportion of homes that have an attached garage is obtained as follows:
Thus, the proportion of homes that have an attached garage is 0.6381.
The level of significance is 0.05.
Therefore, the value of z score at 0.4500
Decision rule:
Reject the null hypothesis if z > 1.645.
The sample size n is 100 and p is 0.60. Therefore, the number of events x is 78.
Step-by-step procedure to find the test statistic using MINITAB software:
- Choose Stat > Basic Statistics > 1 Proportion.
- Choose Summarized data.
- In Number of events, enter 67. In Number of trials, enter 105.
- Enter Hypothesized proportion as 0.60.
- Check Options, enter Confidence level as 95.0.
- Choose greater than in alternative.
- Select Method as Normal approximation.
- Click OK in all dialogue boxes.
Output is obtained as follows:

Thus, the value of the test statistic is 0.80 and the p-value is 0.213.
In this case, the critical value is 1.645 and the test statistic is 0.80.
Here, the test statistic 0.80 is less than the critical value 1.645.
That is, 0.80 < 1.645.
Therefore, do not reject the null hypothesis.
Therefore, people cannot conclude that more than 60% of the homes have a pool.
c.
Develop a
Check whether there is an association between the variables pool and township.
c.
Explanation of Solution
Calculation:
From the given information, the contingency table that shows whether a home has a pool and the township in which the house is located is shown below:
| Pool | Township | |||||
| 1 | 2 | 3 | 4 | 5 | Total | |
| No | 9 | 8 | 7 | 11 | 3 | 38 |
| Yes | 6 | 12 | 18 | 18 | 13 | 67 |
| Total | 15 | 20 | 25 | 29 | 16 | 105 |
The number of degrees of freedom is obtained as follows:
Therefore, the number of degrees of freedom is 4.
Step-by-step procedure to find the critical value using MINITAB software:
- Choose Graph > Probability Distribution Plot > View Probability > OK.
- From Distribution, choose ‘Chi-Square’ distribution.
- Enter Degrees of freedom is 4.
- Click the Shaded Area tab.
- Choose Probability and Right Tail for the region of the curve to shade.
- Enter the data value as 0.05.
- Click OK.
Output using MINITAB software is obtained as follows:
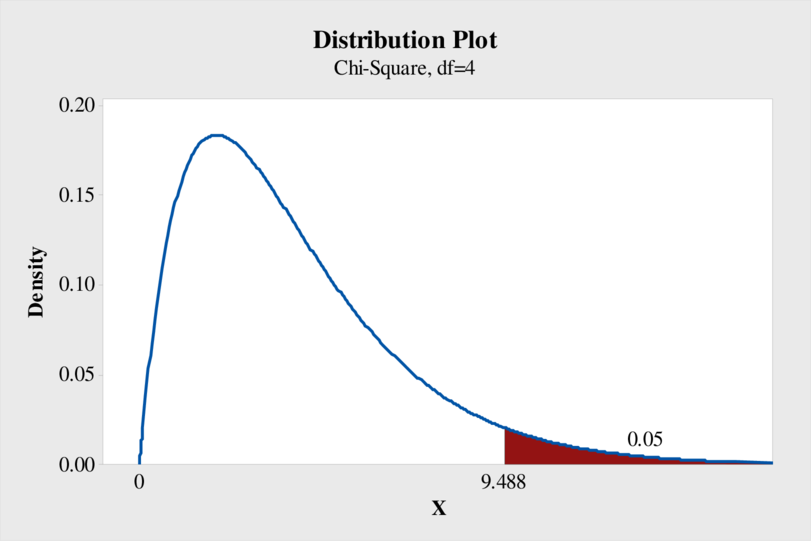
From the output, the critical value of chi-square is 9.488.
The general decision rule is reject the null hypothesis if
Therefore, the decision rule is reject the null hypothesis if
Test statistic:
Step-by-step procedure to find the test statistic using MINITAB software:
- Choose Stat > Tables > Chi-Square Test for Association.
- Choose Summarized data in a two-way table.
- In Columns containing the table, enter the columns of 1, 2, 3, 4 and 5.
- In Rows under Labels for the table, enter the column of Pool.
- Click OK.
Output is obtained as follows:
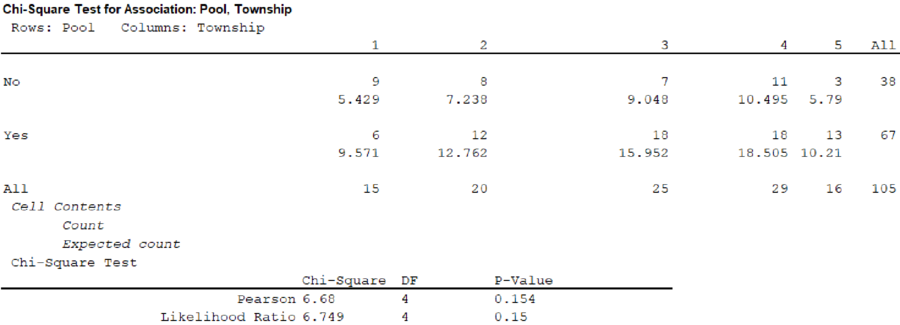
From the output, the test statistic is 6.68.
The critical value is 9.488.
Here, the test statistic is less than the critical value.
That is, 6.68 < 9.488.
Thus, do not reject the null hypothesis.
Therefore, there is no sufficient evidence to conclude that there is an association between the variables pool and township.
d.
Develop a contingency table that shows whether a home has an attached garage and the township in which the house is located.
Check whether there is an association between the variables attached garage and township.
d.
Explanation of Solution
Calculation:
From the given information, the contingency table that shows whether a home has an attached garage and the township in which the house is located is shown below:
| Garage | Township | |||||
| 1 | 2 | 3 | 4 | 5 | Total | |
| No | 6 | 6 | 6 | 6 | 3 | 27 |
| Yes | 9 | 14 | 19 | 23 | 13 | 78 |
| Total | 15 | 20 | 25 | 29 | 16 | 105 |
The number of degrees of freedom is obtained as follows:
Therefore, the number of degrees of freedom is 4.
Step-by-step procedure to find the critical value using MINITAB software:
- Choose Graph > Probability Distribution Plot > View Probability > OK.
- From Distribution, choose ‘Chi-Square’ distribution.
- Enter Degrees of freedom is 4.
- Click the Shaded Area tab.
- Choose Probability and Right Tail for the region of the curve to shade.
- Enter the data value as 0.05.
- Click OK.
Output using MINITAB software is obtained as follows:
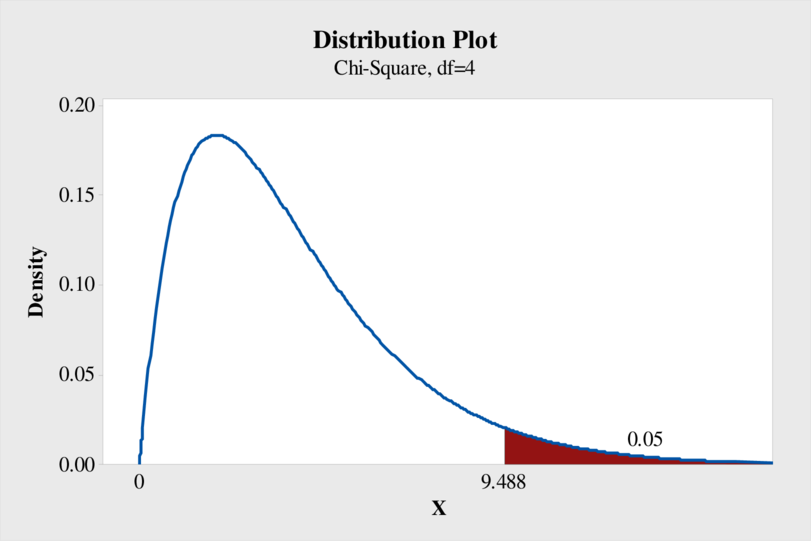
From the output, the critical value of chi-square is 9.488.
The general decision rule is reject the null hypothesis if
Therefore, the decision rule is reject the null hypothesis if
Test statistic:
Step-by-step procedure to find the test statistic using MINITAB software:
- Choose Stat > Tables > Chi-Square Test for Association.
- Choose Summarized data in a two-way table.
- In Columns containing the table, enter the columns of 1, 2, 3, 4 and 5.
- In Rows under Labels for the table, enter the column of Garage.
- Click OK.
Output is obtained as follows:

From the output, the test statistic is 2.623.
The critical value is 9.488.
Here, the test statistic is less than the critical value.
That is, 2.623 < 9.488.
Thus, do not reject the null hypothesis.
Therefore, there is no sufficient evidence to conclude that there is an association between the variables attached garage and township.
Want to see more full solutions like this?
Chapter 15 Solutions
STATISTICAL TECHNIQUES FOR BUSINESS AND
- A company found that the daily sales revenue of its flagship product follows a normal distribution with a mean of $4500 and a standard deviation of $450. The company defines a "high-sales day" that is, any day with sales exceeding $4800. please provide a step by step on how to get the answers in excel Q: What percentage of days can the company expect to have "high-sales days" or sales greater than $4800? Q: What is the sales revenue threshold for the bottom 10% of days? (please note that 10% refers to the probability/area under bell curve towards the lower tail of bell curve) Provide answers in the yellow cellsarrow_forwardFind the critical value for a left-tailed test using the F distribution with a 0.025, degrees of freedom in the numerator=12, and degrees of freedom in the denominator = 50. A portion of the table of critical values of the F-distribution is provided. Click the icon to view the partial table of critical values of the F-distribution. What is the critical value? (Round to two decimal places as needed.)arrow_forwardA retail store manager claims that the average daily sales of the store are $1,500. You aim to test whether the actual average daily sales differ significantly from this claimed value. You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. Showing the calculation is a must. If calculation is missing,so please provide a step by step on the answers Numerical answers in the yellow cellsarrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt






