
Concept explainers
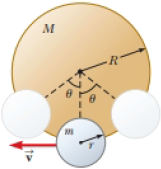
A smaller disk of radius r and mass m is attached rigidly to the face of a second larger disk of radius R and mass M as shown in Figure P15.48. The center of the small disk is located at the edge of the large disk. The large disk is mounted at its center on a frictionless axle. The assembly is rotated through a small angle θ from its equilibrium position and released. (a) Show that the speed of the center of the small disk as it passes through the equilibrium position is
(b) Show that the period of the motion is
Figure P15.48
(a)
The speed of the center of the small disk as it passes through the equilibrium position is
Answer to Problem 48CP
The speed of the center of the small disk as it passes through the equilibrium position is
Explanation of Solution
The radius of the smaller disk is
Consider the figure for the given situation.

Figure (1)
The loss in the potential energy at
Write the expression for the height of the smaller disk from the centre point
Here,
Substitute
Here,
Write the expression for the loss in potential energy.
Here,
Substitute
Write the expression for the moment of inertia of the larger disk about the cylinder axis.
Here,
Write the expression for the moment of inertia of the smaller disk about the cylinder axis.
Here,
Write the expression for the moment of inertia of the smaller disk about the diameter.
Here,
Write the expression for the net moment of inertia of the two disk system.
Here,
Substitute
Write the expression for the angular velocity of the disk.
Here,
The gain in kinetic energy of the system is equal to the sum of the center of mass of the small disk, the rotational energy of the larger disk and the rotational energy of the smaller disk about
Write the expression for the gain in kinetic energy of the system.
Here,
Substitute
Apply conservation law of energy.
Substitute
Further solve the above equation.
Conclusion:
Therefore, the speed of the center of the small disk as it passes through the equilibrium position is
(b)
The period of the motion is
Answer to Problem 48CP
The period of the motion is
Explanation of Solution
As the value of angle at which assembly is rotated is very small.
From the figure, write the expression for the equation of motion.
Substitute
Write the expression for the equation of motion.
Compare equations (1) and (2).
Formula to calculate the period of the motion is,
Here,
Substitute
Substitute
Conclusion:
Therefore, the period of the motion is
Want to see more full solutions like this?
Chapter 15 Solutions
PHYSICS FOR SCI.AND ENGR W/WEBASSIGN
Additional Science Textbook Solutions
Biology: Life on Earth with Physiology (11th Edition)
Principles of Anatomy and Physiology
Biochemistry: Concepts and Connections (2nd Edition)
Cosmic Perspective Fundamentals
Biology: Concepts and Investigations
Fundamentals of Anatomy & Physiology (11th Edition)
- Lab 8 Part 3 PHET Wave Interface simulation. I am having trouble with this part of the lab.arrow_forwardMick and Rick are twins born on Earth in the year 2175. Rick grows up to be an Earth-bound robotics technician while Mick becomes an intergalactic astronaut. Mick leaves the Earth on his first space mission in the year 2200 and travels, according to his clock, for 10 years at a speed of 0.75c. Unfortunately, at this point in his journey, the structure of his ship undergoes mechanical breakdown and the ship explodes. How old is Rick when his brother dies?arrow_forwardHi, I have canceled, why did you charge me again?arrow_forward
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning





