
(a)
The linear programming problem to maximize the profit if the factors are given as below,
| Resource | Regular | Premium | Supreme | Resource Availability |
| Raw gas | ||||
| Production time | ||||
| Storage | ||||
| Profit |
(a)
Answer to Problem 2P
Solution:
The linear programming problem to maximize the profit is,
Subject to the constraints:
Explanation of Solution
Given Information:
The factors are given as below,
| Resource | Regular | Premium | Supreme | Resource Availability |
| Raw gas | ||||
| Production time | ||||
| Storage | ||||
| Profit |
Assume x be the amount of regular resource, y be the amount of premium resource and z be the amount of supreme resource
Therefore, total amount of raw gas is
But the resource availability is
Now, the total production time from the provided table is
But the resource production time is
Now, regular resource can store up to 9 tones. Therefore,
And, premium resource can store up to 6 tones. Therefore,
Also, supreme resource can store up to 5 tones. Therefore,
Since, the amount of resource cannot be negative. Therefore, the positivity constraints are,
Now, the company makes profits of
Subject to the constraints:
(b)
The solution of the linear programming problem,
Subject to the constraints:
By the Simplex method.
(b)
Answer to Problem 2P
Solution:
The values of variables are
Explanation of Solution
Given Information:
The linear programming problem,
Subject to the constraints:
Consider the provided linear programming problem,
Subject to the constraints:
First convert the above problem to standard form by adding slack variables.
As the constraints are subjected to less than condition, non- negative slack variables are added to reach equality.
Let the slack variables be
Thus, the linear programming model would be:
Subject to the constraints:
The above linear programming models consist of three non-basic variables
Now the apply the Simplex method and solve the above problem as:
| Basic | x | y | z | Solution | Intercept |
||||||
| 1 | -150 | -175 | -250 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 7 | 11 | 15 | 1 | 0 | 0 | 0 | 0 | 154 | 10.2667 | |
| 0 | 10 | 8 | 12 | 0 | 1 | 0 | 0 | 0 | 80 | 6.66667 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 9 | ∞ | |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 6 | ∞ | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 5 | 5 |
The negative minimum, P is
The minimum ratio is 5 and it corresponds to basis variable S5. So, the leaving variable is S5.
Therefore, the pivot element is 1.
| Basic | x | y | z | Solution | Intercept |
||||||
| 1 | -150 | -175 | 0 | 0 | 0 | 0 | 0 | 250 | 1250 | ||
| 0 | 7 | 11 | 0 | 1 | 0 | 0 | 0 | -15 | 79 | 7.18182 | |
| 0 | 10 | 8 | 0 | 0 | 1 | 0 | 0 | -12 | 20 | 2.5 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 9 | ∞ | |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 6 | 6 | |
| z | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 5 | ∞ |
The negative minimum, P is
The minimum ratio is 2.5 and it corresponds to basis variable S2. So, the leaving variable is S2.
Therefore, the pivot element is 8.
| Basic | x | y | z | Solution | Intercept |
||||||
| 1 | 68.75 | 0 | 0 | 0 | 21.88 | 0 | 0 | -12.5 | 1687.5 | ||
| 0 | -6.75 | 0 | 0 | 1 | -1.375 | 0 | 0 | 1.5 | 51.5 | 34.3333 | |
| y | 0 | 1.25 | 1 | 0 | 0 | 0.125 | 0 | 0 | -1.5 | 2.5 | -1.66667 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 9 | ∞ | |
| 0 | -1.25 | 0 | 0 | 0 | -0.125 | 0 | 1 | 1.5 | 3.5 | 2.33333 | |
| z | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 5 | 5 |
The negative minimum, P is
The minimum positive ratio is 2.33333 and it corresponds to basis variable S4. So, the leaving variable is S4.
Therefore, the pivot element is 1.5.
| Basic | x | y | z | Solution | ||||||
| 1 | 58.3333 | 0 | 0 | 0 | 20.83 | 0 | 8.33 | 0 | 1716.7 | |
| 0 | -5.5 | 0 | 0 | 1 | -1.25 | 0 | -1 | 0 | 48 | |
| y | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 6 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 9 | |
| 0 | -0.8333 | 0 | 0 | 0 | -0.083 | 0 | 0.67 | 1 | 2.3333 | |
| z | 0 | 0.83333 | 0 | 1 | 0 | 0.083 | 0 | -0.67 | 0 | 2.6667 |
Since
Hence, the values of variables are
(c)
The solution of the linear programming problem,
Subject to the constraints:
By the use of software.
(c)
Answer to Problem 2P
Solution:
The maximum profit is 1716.7 with
Explanation of Solution
Given Information:
The linear programming problem,
Subject to the constraints:
Use excel solver as below, to solve the linear programming,
Step 1: Enter the coefficients of x, y and z for each constraint as below,
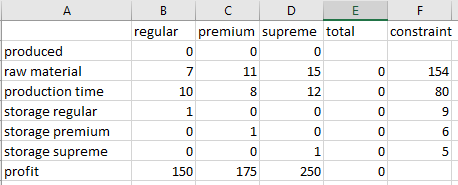
Step 2: Use formulas in column E to find total are as below,

Step 3: click on Solver button under the Data Ribbon. Set the values in the Solver dialogue box as below:
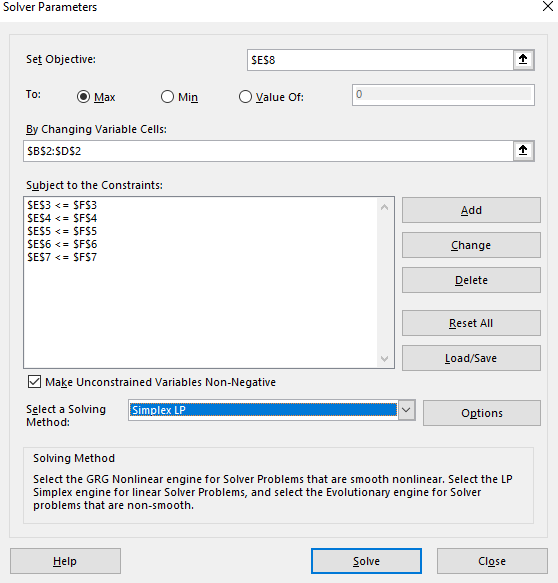
Step 4: Press the solve button.
The result obtained as,
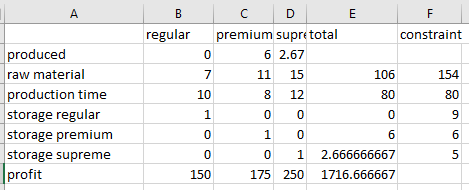
Hence, the maximum value profit is 1716.7 with
(d)
The constraint among increasing raw material, storage or production time that gives the maximum profit.
(d)
Answer to Problem 2P
Solution:
The increasing production time will give the maximum profit.
Explanation of Solution
Given Information:
The linear programming problem,
Subject to the constraints:
To obtain the maximum profit, the shadow price should be high.
Use excel as below to find the shadow price by generating the sensitivity report,
Follow same steps up to the step 4 of part (d) then select the report as sensitivity as below,
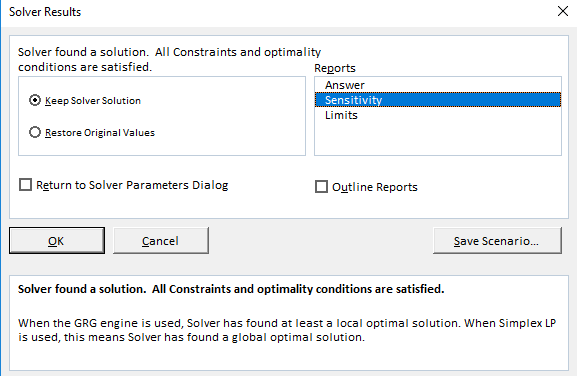
The sensitivity report for the linear programming problem is as follows,
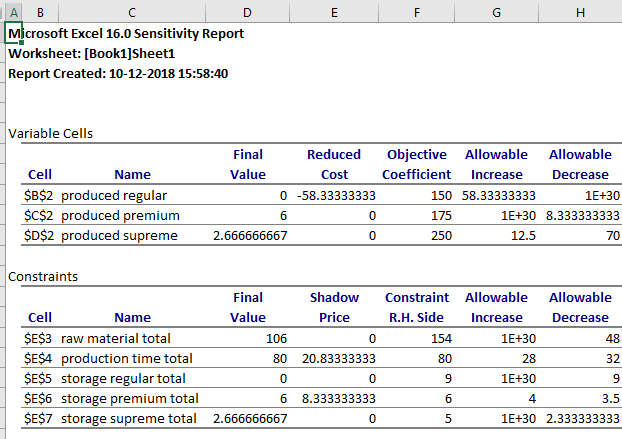
From the above sensitivity report, it is observed that the production time has a high shadow price.
Hence, the production time will give the maximum profit.
Want to see more full solutions like this?
Chapter 15 Solutions
Numerical Methods for Engineers
- 2) Prove that for all integers n > 1. dn 1 (2n)! 1 = dxn 1 - Ꮖ 4 n! (1-x)+/arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
- 3) Let a1, a2, and a3 be arbitrary real numbers, and define an = 3an 13an-2 + An−3 for all integers n ≥ 4. Prove that an = 1 - - - - - 1 - - (n − 1)(n − 2)a3 − (n − 1)(n − 3)a2 + = (n − 2)(n − 3)aı for all integers n > 1.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward1) If f(x) = g¹ (g(x) + a) for some real number a and invertible function g, show that f(x) = (fo fo... 0 f)(x) = g¯¹ (g(x) +na) n times for all integers n ≥ 1.arrow_forwardimage belowarrow_forward
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






