
A recent insurance industry report indicated that 40% of those persons involved in minor traffic accidents this year have been involved in at least one other traffic accident in the last 5 years. An advisory group decided to investigate this claim, believing it was too large. A sample of 200 traffic accidents this year showed 74 persons were also involved in another accident within the last 5 years. Use the .01 significance level.
- (a) Can we use z as the test statistic? Tell why or why not.
- (b) State the null hypothesis and the alternate hypothesis.
- (c) Show the decision rule graphically.
- (d) Compute the value of z and state your decision regarding the null hypothesis.
- (e) Determine and interpret the p-value.
a.
Check whether people can use z as the test statistic and explain the reason.
Answer to Problem 1SR
Yes, people can use z as the test statistic because both nπ and n (1–π) exceed 5.
Explanation of Solution
Requirements to check:
It is given that the sample size n is 100.
For
For
Hence, the requirements are satisfied for using the z-statistic as the binomial distribution.
b.
State the null and alternate hypotheses.
Explanation of Solution
In this case, the test is to check whether less than 40% of the persons involved in minor traffic accidents this year have been involved in at least one other traffic accident in the last 5 years.
Let π represents population proportion of persons involved in minor traffic accidents this year have been involved in at least one other traffic accident in the last 5 years.
Therefore, the null and alternate hypotheses are shown below:
c.
Show the decision rule graphically.
Explanation of Solution
Step-by-step procedure to show the decision rule graphically using MINITAB software:
- Choose Graph > Probability Distribution Plot > View Probability > OK.
- From Distribution, choose ‘Normal’ distribution.
- Enter Mean as 0 and Standard deviation as 1.
- Click the Shaded Area tab.
- Choose Probability and Left Tail for the region of the curve to shade.
- Enter the Probability as 0.01.
- Click OK.
Output using MINITAB software is obtained as follows:
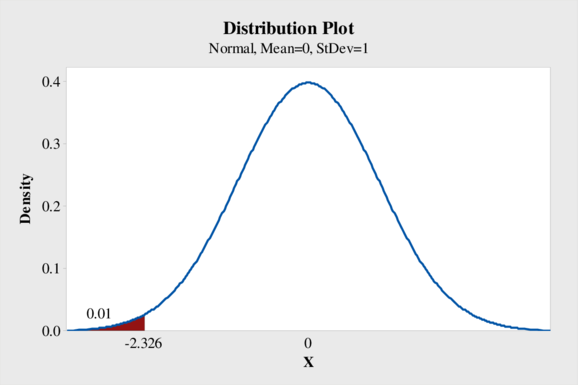
From the output, the critical value is –2.326.
Therefore, the decision rule is rejecting the null hypothesis if test statistic is less than –2.326.
d.
Find the value of z-statistic and the write the decision regarding the null hypothesis.
Answer to Problem 1SR
The value of chi-square is –0.87.
Explanation of Solution
Calculation:
The sample size n is 200 and x is 74.
Step-by-step procedure to find the test statistic using MINITAB software:
- Choose Stat > Basic Statistics > 1 Proportion.
- Choose Summarized data.
- In Number of events, enter 74. In Number of trials, enter 200.
- Enter Hypothesized proportion as 0.40.
- Check Options, enter Confidence level as 99.0.
- Choose less than in alternative.
- Select Method as Normal approximation.
- Click OK in all dialogue boxes.
Output is obtained as follows:

From the output, the value of the test statistic is –0.87.
In this case, the critical values is –2.326 and the test statistic is –0.87.
Here, the test statistic value is less than the critical value.
That is, –0.87 > –2.326.
Therefore, do not reject the null hypothesis.
e.
Find and interpret the p-value.
Explanation of Solution
From the output of Part (d), it can be observed that the p-value is 0.193 and it is more than the level of significance. Therefore, there is no sufficient evidence to conclude that less than 40% of the persons involved in minor traffic accidents this year have been involved in at least one other traffic accident in the last 5 years.
Want to see more full solutions like this?
Chapter 15 Solutions
EBK STATISTICAL TECHNIQUES IN BUSINESS
- 15. This problem extends Problem 20.6. Let X, Y be random variables with finite mean. Show that 00 (P(X ≤ x ≤ Y) - P(X ≤ x ≤ X))dx = E Y — E X.arrow_forward(b) Define a simple random variable. Provide an example.arrow_forward17. (a) Define the distribution of a random variable X. (b) Define the distribution function of a random variable X. (c) State the properties of a distribution function. (d) Explain the difference between the distribution and the distribution function of X.arrow_forward
- 16. (a) Show that IA(w) is a random variable if and only if A E Farrow_forward15. Let 2 {1, 2,..., 6} and Fo({1, 2, 3, 4), (3, 4, 5, 6}). (a) Is the function X (w) = 21(3, 4) (w)+711.2,5,6) (w) a random variable? Explain. (b) Provide a function from 2 to R that is not a random variable with respect to (N, F). (c) Write the distribution of X. (d) Write and plot the distribution function of X.arrow_forward20. Define the o-field R2. Explain its relation to the o-field R.arrow_forward
- 7. Show that An → A as n→∞ I{An} - → I{A} as n→ ∞.arrow_forward7. (a) Show that if A,, is an increasing sequence of measurable sets with limit A = Un An, then P(A) is an increasing sequence converging to P(A). (b) Repeat the same for a decreasing sequence. (c) Show that the following inequalities hold: P (lim inf An) lim inf P(A) ≤ lim sup P(A) ≤ P(lim sup A). (d) Using the above inequalities, show that if A, A, then P(A) + P(A).arrow_forward19. (a) Define the joint distribution and joint distribution function of a bivariate ran- dom variable. (b) Define its marginal distributions and marginal distribution functions. (c) Explain how to compute the marginal distribution functions from the joint distribution function.arrow_forward
- 18. Define a bivariate random variable. Provide an example.arrow_forward6. (a) Let (, F, P) be a probability space. Explain when a subset of ?? is measurable and why. (b) Define a probability measure. (c) Using the probability axioms, show that if AC B, then P(A) < P(B). (d) Show that P(AUB) + P(A) + P(B) in general. Write down and prove the formula for the probability of the union of two sets.arrow_forward21. Prove that: {(a, b), - sa≤barrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL


