Chapter 15, Problem 1RE

Consider the boundary-value problem

$\begin{array}{lll}\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=0,\hfill & 0<x<2,\hfill & 0<y<1\hfill \\ u(0,y)=0,\hfill & u(2,y)=50,\hfill & 0<y<1\hfill \\ u(x,0)=0,\hfill & u(x,1)=0,\hfill & 0<x<2\hfill \end{array}$

Approximate the solution of the differential equation at the interior points of the region with mesh size h = $\frac{1}{2}$. Use Gaussian elimination or Gauss-Seidel iteration.

To determine

The approximate solution of the given differential equation $\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=0$ at the interior points of the region with mesh size $h=\frac{1}{2}$ using Gaussian elimination or Gauss-Seidel iteration.

Answer to Problem 1RE

The approximate solution of the differential equation at the interior points of the region is $\underset{\_}{u_{11}=0.8929,u_{21}=3.5714,u_{31}=13.3928}$.

Explanation of Solution

Formula used:

$u_{ij}=\frac{1}{4}\left[u_{i+1,j}+u_{i,j+1}+u_{i-1,j}+u_{i,j-1}\right]$

Calculation:

Consider the given boundary value problem.

$\begin{array}{l}\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=0,0<x<2,0<y<1\\ u\left(0,y\right)=0,u\left(2,y\right)=50,0<y<1\\ u\left(x,0\right)=0,u\left(x,1\right)=0,0<x<2\end{array}$

For constructing a mesh with size with $h=\frac{1}{2}$, the following values are required.

$\begin{array}{c}{P}_{41}=P\left(4h,h\right)\\ P_{41}=P\left(2,\frac{1}{2}\right)\end{array}$

Since $x=2,y=\frac{1}{2}$, the value of $u\left(2,y\right)$ is evaluated as follows.

$u\left(2,y\right)=50$

Similarly, $P_{12}=P\left(\frac{1}{2},1\right)$ and $u\left(x,1\right)$ gives $u\left(\frac{1}{2},1\right)=0$. All other values are similarly obtained and the figure below shows the values of $u\left(x,y\right)$ along the boundaries.

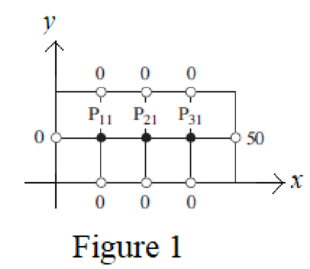
For $P_{11}$ apply the above formula when $i=1$ and $j=1$.

$4u_{11}=\left[u_{21}+u_{12}+u_{01}+u_{10}\right]$

From the given boundary conditions $u_{01}=u\left(0,1\right)=0$, $u_{12}=u\left(\frac{1}{2},1\right)=0$ and $u_{10}=u\left(1,0\right)=0$. Thus, the above equation becomes $u_{21}-4u_{11}=0$.

Repeat this for $P_{21},P_{31}$, which in turn gives three equations with three unknowns as follows.

$\begin{array}{l}{u}_{21}+0+0+0-4u_{11}=0\\ u_{31}+0+u_{11}+0-4u_{21}=0\\ 50+0+u_{21}+0-4u_{31}=0\end{array}$

Since there are less number of unknowns, use Gauss-elimination method to solve the system of equations.

$\left[\begin{array}{ccc}-4& 1& 0\\ 1& -4& 1\\ 0& 1& -4\end{array}\right]\left[\begin{array}{c}{u}_{11}\\ u_{21}\\ u_{31}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ -50\end{array}\right]$

Here, use row column transformations to obtain the values of $u_{11},u_{21},u_{31}$.

$\begin{array}{l}\sim \left[\begin{array}{ccc}1& -0.25& 0\\ 1& -4& 1\\ 0& 1& -4\end{array}|\begin{array}{c}0\\ 0\\ -50\end{array}\right]R_1\to -\frac{R_1}{4}\\ \sim \left[\begin{array}{ccc}1& -0.25& 0\\ 0& -3.75& 1\\ 0& 1& -4\end{array}|\begin{array}{c}0\\ 0\\ -50\end{array}\right]R_2\to R_2-R_1\\ \sim \left[\begin{array}{ccc}1& -0.25& 0\\ 0& 1& -0.267\\ 0& 1& -4\end{array}|\begin{array}{c}0\\ 0\\ -50\end{array}\right]R_2\to -\frac{R_2}{3.75}\\ \sim \left[\begin{array}{ccc}1& 0& -0.067\\ 0& 1& -0.267\\ 0& 1& -3.733\end{array}|\begin{array}{c}0\\ 0\\ -50\end{array}\right]R_1\to R_1+0.25R_2\end{array}$

Further reduce the matrix as follows.

$\begin{array}{l}\sim \left[\begin{array}{ccc}1& 0& -0.067\\ 0& 1& -0.267\\ 0& 1& 1\end{array}|\begin{array}{c}0\\ 0\\ 13.3928\end{array}\right]R_3\to -\frac{R_3}{3.733}\\ \sim \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 1& 1\end{array}|\begin{array}{c}0.8929\\ 3.5714\\ 13.3928\end{array}\right]R_1\to R_1+0.067R_3\end{array}$

Therefore, the approximate solution of the differential equation at the interior points of the region is $\underset{\_}{u_{11}=0.8929,u_{21}=3.5714,u_{31}=13.3928}$.