
A company makes two types of products, A and B. These products are produced during a 40-hr work week and then shipped out at the end of the week. They require 20 and 5 kg of raw material per kg of product, respectively, and the company has access to 9500 kg of raw material per week. Only one product can be created at a time with production times for each of 0.04 and 0.12 hr, respectively. The plant can only store 550 kg of total product per week. Finally, the company makes profits of $45 and $20 on each unit of A and B, respectively. Each unit of product is equivalent to a kg.
(a) Set up the linear programming problem to maximize profit.
(b) Solve the linear programming problem graphically.
(c) Solve the linear programming problem with the simplex method.
(d) Solve the problem with a software package.
(e) Evaluate which of the following options will raise profits the most: increasing raw material, storage, or production time.
(a)
The linear programming problem to maximize the profit if the company makes profits of $45 on each unit of A and $20 on each unit of B.
Answer to Problem 1P
Solution:
The linear programming problem to maximize the profit is,
Subject to the constraints:
Explanation of Solution
Given Information:
Product A and B are produced during a 40-hr of work week.
Company has access to 9500 kg of raw material per week.
Company required 20 kg of raw material per kg of product A and 5 kg of raw material per kg of product B.
One product of A can be created in 0.04 hour and one product of B can be created in 0.12 hour.
Plant can store 550 kg of total product per week.
And, the company makes profits of $45 on each unit of A and $20 on each unit of B.
Assume
Therefore, total number of products is
But plant can store 550 kg of total product per week. Therefore, the storage constrain is,
Company required 20 kg of raw material per kg of product A and 5 kg of raw material per kg of product B. Therefore, total raw material per week is,
But the company has access to 9500 kg of raw material per week. Therefore, raw material constraint is,
One product of A can be created in 0.04 hour and one product of B can be created in 0.12 hour. Therefore, the total production time is,
Since, product A and B are produced during a 40-hr of work week. Therefore, the production time constraint is,
Since, the amount of product cannot be negative. Therefore, the positivity constraint is,
Now, the company makes profits of $45 on each unit of A and $20 on each unit of B. Therefore, maximum profit is,
Subject to the constraints:
(b)
To calculate: The solution of the linear programming problem,
Subject to the constraints:
By the graphical method.
Answer to Problem 1P
Solution:
The maximum value of P is approximately
Explanation of Solution
Given Information:
The linear programming problem,
Subject to the constraints:
Formula used:
The equation of a straight line is,
Where, m is the slope and C is the intercept of y.
Calculation:
Consider the linear programming problem,
Subject to the constraints:
Reformulate the constraints to straight lines by replacing inequality by equal sign and solving for
The above equations are the equation of straight lines and represent the constraints.
The value of P in the objective function
Plot all the straight lines.
The graph obtained is,
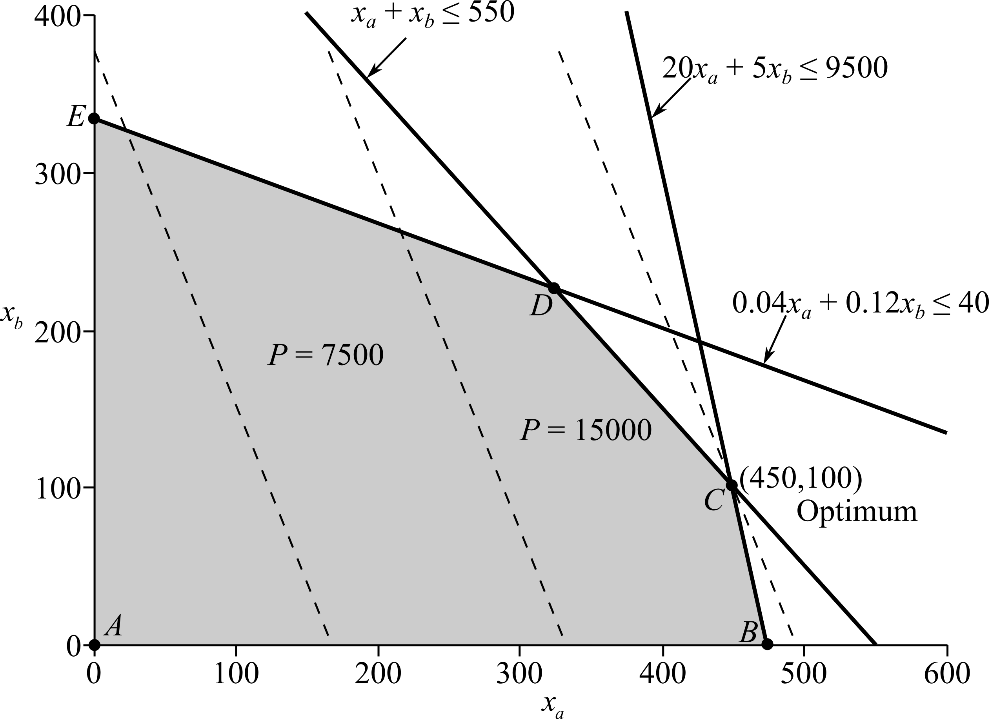
Hence, the maximum value of P is approximately
(c)
The solution of the linear programming problem,
Subject to the constraints:
By the Simplex method.
Answer to Problem 1P
Solution:
The values of variables are
Explanation of Solution
Given Information:
The linear programming problem,
Subject to the constraints:
Consider the provided linear programming problem,
Subject to the constraints:
First convert the above problem to standard form by adding slack variables.
As the constraints are subjected to less than condition, non- negative slack variables are added to reach equality.
Let the slack variables be
Thus, the linear programming model would be:
Subject to the constraints:
The above linear programming models consist of three non-basic variables
Now the apply the Simplex method and solve the above problem as:
| Basic | Solution | Intercept | ||||||
| 1 | -45 | -20 | 0 | 0 | 0 | 0 | ||
| 0 | 20 | 5 | 1 | 0 | 0 | 9500 | 475 | |
| 0 | 0.04 | 0.12 | 0 | 1 | 0 | 40 | 1000 | |
| 0 | 1 | 1 | 0 | 0 | 1 | 550 | 550 |
The negative minimum, P is
The minimum ratio is 475 and it corresponds to basis variable S 1. So, the leaving variable is S 1.
Therefore, the pivot element is 20.
| Basic | Solution | Intercept | ||||||
| 1 | 0 | -8.75 | 2.25 | 0 | 0 | 21375 | ||
| 0 | 1 | 0.25 | 0.05 | 0 | 0 | 475 | 1900 | |
| 0 | 0 | 0.11 | -0.002 | 1 | 0 | 21 | 190.9090 | |
| 0 | 0 | 0.75 | -0.05 | 0 | 1 | 75 | 100 |
The negative minimum, P is
The minimum ratio is 100 and it corresponds to basis variable S 3. So, the leaving variable is S 3.
Therefore, the pivot element is 0.75.
| Basic | Solution | Intercept | ||||||
| 1 | 0 | 0 | 1.6667 | 0 | 11.6667 | 22250 | ||
| 0 | 1 | 0 | 0.0667 | 0 | -0.3333 | 450 | 1900 | |
| 0 | 0 | 0 | 0.0053 | 1 | -0.1467 | 10 | 190.9090 | |
| 0 | 0 | 1 | -0.0667 | 0 | 1.3333 | 100 | 100 |
Since
Hence, the values of variables are
(d)
The solution of the linear programming problem,
Subject to the constraints:
By the use of software.
Answer to Problem 1P
Solution:
The maximum profitis
Explanation of Solution
Given Information:
The linear programming problem,
Subject to the constraints:
Use excel solver as below, to solve the linear programming,
Step 1: Enter the coefficients of
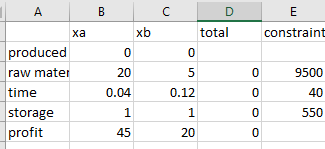
Step 2: Use formulas in column D to find total are as below,
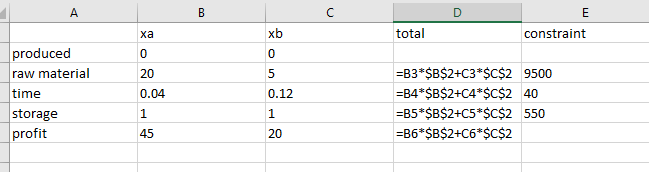
Step 3: click on Solver button under the Data Ribbon. Set the values in pertinent cells of Solver dialogue box as below:
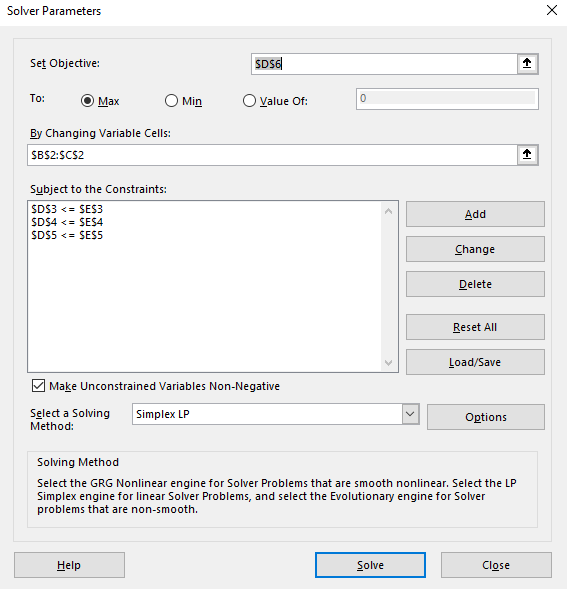
Step 4: Press the solve button.
The result obtained as,
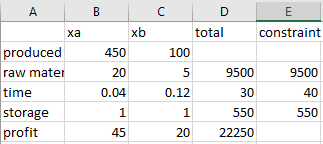
Hence, the maximum value profitis
(e)
The constraint among increasing raw material, storage or production time that gives the maximum profit.
Answer to Problem 1P
Solution:
The storage will give the maximum profit.
Explanation of Solution
Given Information:
The linear programming problem,
Subject to the constraints:
To obtain the maximum profit, the shadow price should be high.
Use excel as below to find the shadow price by generating the sensitivity report,
Follow same steps up to the step 4 of part (d) then select the report as sensitivity as below,
The sensitivity report for the linear programming problem is as follows:
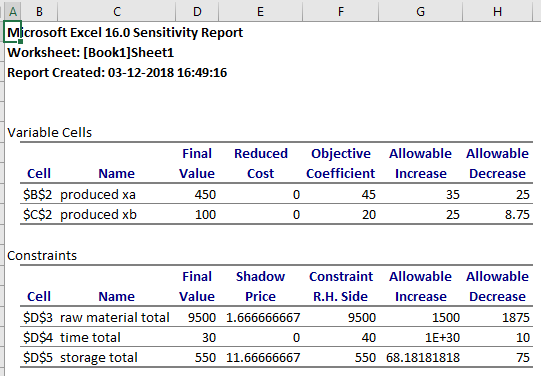
From the above sensitivity report, it is observed that the storage has a high shadow price.
Hence, the storage will give the maximum profit.
Want to see more full solutions like this?
Chapter 15 Solutions
Numerical Methods for Engineers
- Page < 1 of 2 - ZOOM + 1) a) Find a matrix P such that PT AP orthogonally diagonalizes the following matrix A. = [{² 1] A = b) Verify that PT AP gives the correct diagonal form. 2 01 -2 3 2) Given the following matrices A = -1 0 1] an and B = 0 1 -3 2 find the following matrices: a) (AB) b) (BA)T 3) Find the inverse of the following matrix A using Gauss-Jordan elimination or adjoint of the matrix and check the correctness of your answer (Hint: AA¯¹ = I). [1 1 1 A = 3 5 4 L3 6 5 4) Solve the following system of linear equations using any one of Cramer's Rule, Gaussian Elimination, Gauss-Jordan Elimination or Inverse Matrix methods and check the correctness of your answer. 4x-y-z=1 2x + 2y + 3z = 10 5x-2y-2z = -1 5) a) Describe the zero vector and the additive inverse of a vector in the vector space, M3,3. b) Determine if the following set S is a subspace of M3,3 with the standard operations. Show all appropriate supporting work.arrow_forwardUsing Karnaugh maps and Gray coding, reduce the following circuit represented as a table and write the final circuit in simplest form (first in terms of number of gates then in terms of fan-in of those gates).arrow_forwardConsider the alphabet {a, b, c}.• Design a regular expression that recognizes all strings over {a, b, c} that have at least three nonconsec-utive c characters (two characters are non-consecutive if there is at least one character between them)and at least one a character.• Explain how your regular expression recognizes the string cbbcccac by clearly identifying which partsof the string match to the components of your regular expressionarrow_forward
- Complex Analysis 2 z3+3 Q1: Evaluate cz(z-i)² the Figure. First exam 2024-2025 dz, where C is the figure-eight contour shown inarrow_forwardConstruct a state-level description (i.e., a state diagram with transitions) for aTuring machine that decides the language {a^(n)b^(2n)c^(n) | n ∈ N}.arrow_forwardFind the sum of products expansion of the function F (x, y, z) = ̄x · y + x · z in two ways: (i) using a table; and (ii) using Boolean identitiesarrow_forward
- The NOR operator, denoted as ↓, behaves as 0 ↓ 0 = 1, 0 ↓ 1 = 0, 1 ↓ 0 = 0,1 ↓ 1 = 0. Show that the any Boolean function over any number of variables can be expressed using onlyNOR operators (in addition to those variables and constants). HINT: Recall that any Boolean function hasa representation as a sum of products expansionarrow_forwardConsider the Turing machine given in lecture which decides the languageB = {w#w | w is a binary string}.Simulate the Turing machine to show that the string 1001#1001 will be accepted by the Turing machine. Show all steps.arrow_forwardQ/Find the Laurent series of (2-3) cos↓ around z = 1. 2-1arrow_forward
- #1). A technique is given with 150 mAs is 40 kV and produces an EI value = 400. Find the new EI value, if mAs is 75 and 34 kV are used.arrow_forwardQ3: Answer the following: (i) Let f(z) is an analytic function in a simply connected domain S and y is a simple, closed, positively oriented contour lying in S. Prove that f, f(z)dz = 0.arrow_forwardUse the method of undetermined coefficients to solve the given nonhomogeneous system.X' = −1 33 −1 X + −4t2t + 2 X(t) =arrow_forward

 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning





