CALCULUS (CLOTH)
CALCULUS (CLOTH)
4th Edition
ISBN: 9781319050733
Author: Rogawski
Publisher: MAC HIGHER
bartleby

Concept explainers

Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 …
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experime…
bartleby

Videos

Question
Book Icon
Chapter 15, Problem 1CRE
To determine

(a)

Sketch the domain of the function f(x,y) = x2− y2x + 3 

Expert Solution
Check Mark

Answer to Problem 1CRE

Solution:Domain of the function f(x,y) = x2− y2x + 3  is D = {(x, y) : x ≥ ±y  ; x ≠ - 3 }

Explanation of Solution

Domain: The domain of the function is defined as the set of complete possible values which will make the function work and gives output as real values.

Given: A function as f(x,y) = x2− y2x + 3 

Formula:

a. Domain of Square root function, x is given as x  ≥ 0 

b. The expression in the denominator can never be zero.

Calculation:

Given function is f(x,y) = x2− y2x + 3 

Domain of the functionf(x,y) = x2− y2x + 3 :

To find the domain, set the expression the expression inside the square root greater than equal to zero and the expression in the denominator not equal to zero.

x + 3 ≠ 0  And x2− y2≥ 0 

x ≠ - 3  And x2 ≥ y2 

x ≥ ±y 

Thus, domain of the function is D = {(x, y) : x ≥ ±y  ; x ≠ - 3 }

Graph is as follows:

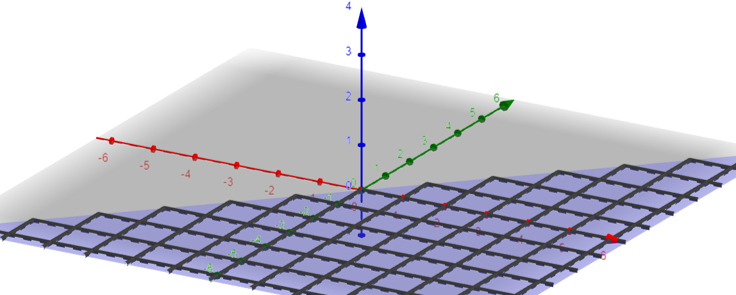
CALCULUS (CLOTH), Chapter 15, Problem 1CRE

Conclusion: Domain of the function f(x,y) = x2− y2x + 3  is D = {(x, y) : x ≥ ±y  ; x ≠ - 3 }

To determine

(b)

The value of f(3,1) and f(−5,−3) for the function f(x,y) = x2− y2x + 3 

Expert Solution
Check Mark

Answer to Problem 1CRE

Solution: The value of f(3,1) = 23 and f(−5,−3) = −2

Explanation of Solution

Domain: The domain of the function is defined as the set of complete possible values which will make the function work and gives output as real values.

Given: A function as f(x,y) = x2− y2x + 3 

Calculation:

Given function is f(x,y,z) = x2− y2x + 3 

f(3,1) = (3)2− (1)2(3) + 3 = 9 − 13 + 3 = 86 = 226 = 23

f(−5,−3) = (−5)2− (−3)2(−5) + 3 = 25 − 9- 5 + 3 = 16−2 = 4−2 = −2

Conclusion: The value of f(3,1) = 23 and f(−5,−3) = −2

To determine

(c)

A point (x, y) such that f(x,y)=1 for the function f(x,y) = x2− y2x + 3 

Expert Solution
Check Mark

Answer to Problem 1CRE

Solution: The point (x, y) such that f(x,y)=1 for the function f(x,y) = x2− y2x + 3  Are (−3,33) and (−3,−33)

Explanation of Solution

Domain: The domain of the function is defined as the set of complete possible values which will make the function work and gives output as real values.

Given: A function as

f(x,y) = x2− y2x + 3 

Calculation:

Given function is f(x,y,z) = x2− y2x + 3 

Also, f(x,y)=1

f(x,y,z) = x2− y2x + 3 = 1

x2− y2x + 3 = 1

x2− y2 = x + 3

Squaring both the sides, we get

x2− y2 = (x + 3)2

x2− y2 = x2 + 9 + 6x

 y2 = -( 9 + 6x)

Let x = −6,

Then  y2 = -( 9 + 6x)=−(9−36)=27

Thus, y = ±33

Points are (−3,33) and (−3,−33)

Conclusion: The point (x, y) such that f(x,y)=1 for the function f(x,y) = x2− y2x + 3  are (−3,33) and (−3,−33)

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Previous
Chapter 15.8, Problem 56E
Next
Chapter 15, Problem 2CRE
Students have asked these similar questions
3. Solve the inequality, and give your answer in interval notation. - (x − 4)³ (x + 1) ≥ 0
1. Find the formula to the polynomial at right. Show all your work. (4 points) 1- 2 3 сл 5 6 -4 -3 -2 -1 0 2 3
2. Find the leading term (2 points): f(x) = −3x(2x − 1)²(x+3)³ -

Chapter 15 Solutions

CALCULUS (CLOTH)

Ch. 15.1 - Prob. 1PQCh. 15.1 - Prob. 2PQCh. 15.1 - Prob. 3PQCh. 15.1 - Prob. 4PQCh. 15.1 - Prob. 5PQCh. 15.1 - Prob. 1ECh. 15.1 - Prob. 2ECh. 15.1 - Prob. 3ECh. 15.1 - Prob. 4ECh. 15.1 - Prob. 5E
Ch. 15.1 - Prob. 6ECh. 15.1 - Prob. 7ECh. 15.1 - Prob. 8ECh. 15.1 - Prob. 9ECh. 15.1 - Prob. 10ECh. 15.1 - Prob. 11ECh. 15.1 - Prob. 12ECh. 15.1 - Prob. 13ECh. 15.1 - Prob. 14ECh. 15.1 - Prob. 15ECh. 15.1 - Prob. 16ECh. 15.1 - Prob. 17ECh. 15.1 - Prob. 18ECh. 15.1 - Prob. 19ECh. 15.1 - Prob. 20ECh. 15.1 - Prob. 21ECh. 15.1 - Prob. 22ECh. 15.1 - Prob. 23ECh. 15.1 - Prob. 24ECh. 15.1 - Prob. 25ECh. 15.1 - Prob. 26ECh. 15.1 - Prob. 27ECh. 15.1 - Prob. 28ECh. 15.1 - Prob. 29ECh. 15.1 - Prob. 30ECh. 15.1 - Prob. 31ECh. 15.1 - Prob. 32ECh. 15.1 - Prob. 33ECh. 15.1 - Prob. 34ECh. 15.1 - Prob. 35ECh. 15.1 - Prob. 36ECh. 15.1 - Prob. 37ECh. 15.1 - Prob. 38ECh. 15.1 - Prob. 39ECh. 15.1 - Prob. 40ECh. 15.1 - Prob. 41ECh. 15.1 - Prob. 42ECh. 15.1 - Prob. 43ECh. 15.1 - Prob. 44ECh. 15.1 - Prob. 45ECh. 15.1 - Prob. 46ECh. 15.1 - Prob. 47ECh. 15.1 - Prob. 48ECh. 15.1 - Prob. 49ECh. 15.1 - Prob. 50ECh. 15.1 - Prob. 51ECh. 15.1 - Prob. 52ECh. 15.1 - Prob. 53ECh. 15.1 - Prob. 54ECh. 15.1 - Prob. 55ECh. 15.1 - Prob. 56ECh. 15.1 - Prob. 57ECh. 15.1 - Prob. 58ECh. 15.1 - Prob. 59ECh. 15.1 - Prob. 60ECh. 15.1 - Prob. 61ECh. 15.2 - Prob. 1PQCh. 15.2 - Prob. 2PQCh. 15.2 - Prob. 3PQCh. 15.2 - Prob. 4PQCh. 15.2 - Prob. 1ECh. 15.2 - Prob. 2ECh. 15.2 - Prob. 3ECh. 15.2 - Prob. 4ECh. 15.2 - Prob. 5ECh. 15.2 - Prob. 6ECh. 15.2 - Prob. 7ECh. 15.2 - Prob. 8ECh. 15.2 - Prob. 9ECh. 15.2 - Prob. 10ECh. 15.2 - Prob. 11ECh. 15.2 - Prob. 12ECh. 15.2 - Prob. 13ECh. 15.2 - Prob. 14ECh. 15.2 - Prob. 15ECh. 15.2 - Prob. 16ECh. 15.2 - Prob. 17ECh. 15.2 - Prob. 18ECh. 15.2 - Prob. 19ECh. 15.2 - Prob. 20ECh. 15.2 - Prob. 21ECh. 15.2 - Prob. 22ECh. 15.2 - Prob. 23ECh. 15.2 - Prob. 24ECh. 15.2 - Prob. 25ECh. 15.2 - Prob. 26ECh. 15.2 - Prob. 27ECh. 15.2 - Prob. 28ECh. 15.2 - Prob. 29ECh. 15.2 - Prob. 30ECh. 15.2 - Prob. 31ECh. 15.2 - Prob. 32ECh. 15.2 - Prob. 33ECh. 15.2 - Prob. 34ECh. 15.2 - Prob. 35ECh. 15.2 - Prob. 36ECh. 15.2 - Prob. 37ECh. 15.2 - Prob. 38ECh. 15.2 - Prob. 39ECh. 15.2 - Prob. 40ECh. 15.2 - Prob. 41ECh. 15.2 - Prob. 42ECh. 15.2 - Prob. 43ECh. 15.2 - Prob. 44ECh. 15.2 - Prob. 45ECh. 15.2 - Prob. 46ECh. 15.2 - Prob. 47ECh. 15.2 - Prob. 48ECh. 15.2 - Prob. 49ECh. 15.2 - Prob. 50ECh. 15.2 - Prob. 51ECh. 15.3 - Prob. 1PQCh. 15.3 - Prob. 2PQCh. 15.3 - Prob. 3PQCh. 15.3 - Prob. 4PQCh. 15.3 - Prob. 5PQCh. 15.3 - Prob. 1ECh. 15.3 - Prob. 2ECh. 15.3 - Prob. 3ECh. 15.3 - Prob. 4ECh. 15.3 - Prob. 5ECh. 15.3 - Prob. 6ECh. 15.3 - Prob. 7ECh. 15.3 - Prob. 8ECh. 15.3 - Prob. 9ECh. 15.3 - Prob. 10ECh. 15.3 - Prob. 11ECh. 15.3 - Prob. 12ECh. 15.3 - Prob. 13ECh. 15.3 - Prob. 14ECh. 15.3 - Prob. 15ECh. 15.3 - Prob. 16ECh. 15.3 - Prob. 17ECh. 15.3 - Prob. 18ECh. 15.3 - Prob. 19ECh. 15.3 - Prob. 20ECh. 15.3 - Prob. 21ECh. 15.3 - Prob. 22ECh. 15.3 - Prob. 23ECh. 15.3 - Prob. 24ECh. 15.3 - Prob. 25ECh. 15.3 - Prob. 26ECh. 15.3 - Prob. 27ECh. 15.3 - Prob. 28ECh. 15.3 - Prob. 29ECh. 15.3 - Prob. 30ECh. 15.3 - Prob. 31ECh. 15.3 - Prob. 32ECh. 15.3 - Prob. 33ECh. 15.3 - Prob. 34ECh. 15.3 - Prob. 35ECh. 15.3 - Prob. 36ECh. 15.3 - Prob. 37ECh. 15.3 - Prob. 38ECh. 15.3 - Prob. 39ECh. 15.3 - Prob. 40ECh. 15.3 - Prob. 41ECh. 15.3 - Prob. 42ECh. 15.3 - Prob. 43ECh. 15.3 - Prob. 44ECh. 15.3 - Prob. 45ECh. 15.3 - Prob. 46ECh. 15.3 - Prob. 47ECh. 15.3 - Prob. 48ECh. 15.3 - Prob. 49ECh. 15.3 - Prob. 50ECh. 15.3 - Prob. 51ECh. 15.3 - Prob. 52ECh. 15.3 - Prob. 53ECh. 15.3 - Prob. 54ECh. 15.3 - Prob. 55ECh. 15.3 - Prob. 56ECh. 15.3 - Prob. 57ECh. 15.3 - Prob. 58ECh. 15.3 - Prob. 59ECh. 15.3 - Prob. 60ECh. 15.3 - Prob. 61ECh. 15.3 - Prob. 62ECh. 15.3 - Prob. 63ECh. 15.3 - Prob. 64ECh. 15.3 - Prob. 65ECh. 15.3 - Prob. 66ECh. 15.3 - Prob. 67ECh. 15.3 - Prob. 68ECh. 15.3 - Prob. 69ECh. 15.3 - Prob. 70ECh. 15.3 - Prob. 71ECh. 15.3 - Prob. 72ECh. 15.3 - Prob. 73ECh. 15.3 - Prob. 74ECh. 15.3 - Prob. 75ECh. 15.3 - Prob. 76ECh. 15.3 - Prob. 77ECh. 15.3 - Prob. 78ECh. 15.3 - Prob. 79ECh. 15.3 - Prob. 80ECh. 15.4 - Prob. 1PQCh. 15.4 - Prob. 2PQCh. 15.4 - Prob. 3PQCh. 15.4 - Prob. 4PQCh. 15.4 - Prob. 5PQCh. 15.4 - Prob. 6PQCh. 15.4 - Prob. 1ECh. 15.4 - Prob. 2ECh. 15.4 - Prob. 3ECh. 15.4 - Prob. 4ECh. 15.4 - Prob. 5ECh. 15.4 - Prob. 6ECh. 15.4 - Prob. 7ECh. 15.4 - Prob. 8ECh. 15.4 - Prob. 9ECh. 15.4 - Prob. 10ECh. 15.4 - Prob. 11ECh. 15.4 - Prob. 12ECh. 15.4 - Prob. 13ECh. 15.4 - Prob. 14ECh. 15.4 - Prob. 15ECh. 15.4 - Prob. 16ECh. 15.4 - Prob. 17ECh. 15.4 - Prob. 18ECh. 15.4 - Prob. 19ECh. 15.4 - Prob. 20ECh. 15.4 - Prob. 21ECh. 15.4 - Prob. 22ECh. 15.4 - Prob. 23ECh. 15.4 - Prob. 24ECh. 15.4 - Prob. 25ECh. 15.4 - Prob. 26ECh. 15.4 - Prob. 27ECh. 15.4 - Prob. 28ECh. 15.4 - Prob. 29ECh. 15.4 - Prob. 30ECh. 15.4 - Prob. 31ECh. 15.4 - Prob. 32ECh. 15.4 - Prob. 33ECh. 15.4 - Prob. 34ECh. 15.4 - Prob. 35ECh. 15.4 - Prob. 36ECh. 15.4 - Prob. 37ECh. 15.4 - Prob. 38ECh. 15.4 - Prob. 39ECh. 15.4 - Prob. 40ECh. 15.4 - Prob. 41ECh. 15.4 - Prob. 42ECh. 15.4 - Prob. 43ECh. 15.4 - Prob. 44ECh. 15.4 - Prob. 45ECh. 15.4 - Prob. 46ECh. 15.4 - Prob. 47ECh. 15.5 - Prob. 1PQCh. 15.5 - Prob. 2PQCh. 15.5 - Prob. 3PQCh. 15.5 - Prob. 4PQCh. 15.5 - Prob. 5PQCh. 15.5 - Prob. 1ECh. 15.5 - Prob. 2ECh. 15.5 - Prob. 3ECh. 15.5 - Prob. 4ECh. 15.5 - Prob. 5ECh. 15.5 - Prob. 6ECh. 15.5 - Prob. 7ECh. 15.5 - Prob. 8ECh. 15.5 - Prob. 9ECh. 15.5 - Prob. 10ECh. 15.5 - Prob. 11ECh. 15.5 - Prob. 12ECh. 15.5 - Prob. 13ECh. 15.5 - Prob. 14ECh. 15.5 - Prob. 15ECh. 15.5 - Prob. 16ECh. 15.5 - Prob. 17ECh. 15.5 - Prob. 18ECh. 15.5 - Prob. 19ECh. 15.5 - Prob. 20ECh. 15.5 - Prob. 21ECh. 15.5 - Prob. 22ECh. 15.5 - Prob. 23ECh. 15.5 - Prob. 24ECh. 15.5 - Prob. 25ECh. 15.5 - Prob. 26ECh. 15.5 - Prob. 27ECh. 15.5 - Prob. 28ECh. 15.5 - Prob. 29ECh. 15.5 - Prob. 30ECh. 15.5 - Prob. 31ECh. 15.5 - Prob. 32ECh. 15.5 - Prob. 33ECh. 15.5 - Prob. 34ECh. 15.5 - Prob. 35ECh. 15.5 - Prob. 36ECh. 15.5 - Prob. 37ECh. 15.5 - Prob. 38ECh. 15.5 - Prob. 39ECh. 15.5 - Prob. 40ECh. 15.5 - Prob. 41ECh. 15.5 - Prob. 42ECh. 15.5 - Prob. 43ECh. 15.5 - Prob. 44ECh. 15.5 - Prob. 45ECh. 15.5 - Prob. 46ECh. 15.5 - Prob. 47ECh. 15.5 - Prob. 48ECh. 15.5 - Prob. 49ECh. 15.5 - Prob. 50ECh. 15.5 - Prob. 52ECh. 15.5 - Prob. 53ECh. 15.5 - Prob. 54ECh. 15.5 - Prob. 55ECh. 15.5 - Prob. 56ECh. 15.5 - Prob. 57ECh. 15.5 - Prob. 58ECh. 15.5 - Prob. 59ECh. 15.5 - Prob. 60ECh. 15.5 - Prob. 61ECh. 15.5 - Prob. 62ECh. 15.5 - Prob. 63ECh. 15.5 - Prob. 64ECh. 15.5 - Prob. 65ECh. 15.5 - Prob. 66ECh. 15.5 - Prob. 67ECh. 15.5 - Prob. 68ECh. 15.5 - Prob. 69ECh. 15.5 - Prob. 70ECh. 15.5 - Prob. 71ECh. 15.5 - Prob. 72ECh. 15.5 - Prob. 73ECh. 15.5 - Prob. 74ECh. 15.5 - Prob. 75ECh. 15.5 - Prob. 76ECh. 15.5 - Prob. 77ECh. 15.6 - Prob. 1PQCh. 15.6 - Prob. 2PQCh. 15.6 - Prob. 3PQCh. 15.6 - Prob. 4PQCh. 15.6 - Prob. 5PQCh. 15.6 - Prob. 6PQCh. 15.6 - Prob. 1ECh. 15.6 - Prob. 2ECh. 15.6 - Prob. 3ECh. 15.6 - Prob. 4ECh. 15.6 - Prob. 5ECh. 15.6 - Prob. 6ECh. 15.6 - Prob. 7ECh. 15.6 - Prob. 8ECh. 15.6 - Prob. 9ECh. 15.6 - Prob. 10ECh. 15.6 - Prob. 11ECh. 15.6 - Prob. 12ECh. 15.6 - Prob. 13ECh. 15.6 - Prob. 14ECh. 15.6 - Prob. 15ECh. 15.6 - Prob. 16ECh. 15.6 - Prob. 17ECh. 15.6 - Prob. 18ECh. 15.6 - Prob. 19ECh. 15.6 - Prob. 20ECh. 15.6 - Prob. 21ECh. 15.6 - Prob. 22ECh. 15.6 - Prob. 23ECh. 15.6 - Prob. 24ECh. 15.6 - Prob. 25ECh. 15.6 - Prob. 26ECh. 15.6 - Prob. 27ECh. 15.6 - Prob. 28ECh. 15.6 - Prob. 29ECh. 15.6 - Prob. 30ECh. 15.6 - Prob. 31ECh. 15.6 - Prob. 32ECh. 15.6 - Prob. 33ECh. 15.6 - Prob. 34ECh. 15.6 - Prob. 35ECh. 15.6 - Prob. 36ECh. 15.6 - Prob. 37ECh. 15.6 - Prob. 38ECh. 15.6 - Prob. 39ECh. 15.6 - Prob. 40ECh. 15.6 - Prob. 41ECh. 15.6 - Prob. 42ECh. 15.6 - Prob. 43ECh. 15.6 - Prob. 44ECh. 15.6 - Prob. 45ECh. 15.6 - Prob. 46ECh. 15.6 - Prob. 47ECh. 15.6 - Prob. 48ECh. 15.6 - Prob. 49ECh. 15.6 - Prob. 50ECh. 15.6 - Prob. 51ECh. 15.6 - Prob. 52ECh. 15.6 - Prob. 53ECh. 15.6 - Prob. 54ECh. 15.6 - Prob. 55ECh. 15.7 - Prob. 1PQCh. 15.7 - Prob. 2PQCh. 15.7 - Prob. 3PQCh. 15.7 - Prob. 1ECh. 15.7 - Prob. 2ECh. 15.7 - Prob. 3ECh. 15.7 - Prob. 4ECh. 15.7 - Prob. 5ECh. 15.7 - Prob. 6ECh. 15.7 - Prob. 7ECh. 15.7 - Prob. 8ECh. 15.7 - Prob. 9ECh. 15.7 - Prob. 10ECh. 15.7 - Prob. 11ECh. 15.7 - Prob. 12ECh. 15.7 - Prob. 13ECh. 15.7 - Prob. 14ECh. 15.7 - Prob. 15ECh. 15.7 - Prob. 16ECh. 15.7 - Prob. 17ECh. 15.7 - Prob. 18ECh. 15.7 - Prob. 19ECh. 15.7 - Prob. 20ECh. 15.7 - Prob. 21ECh. 15.7 - Prob. 22ECh. 15.7 - Prob. 23ECh. 15.7 - Prob. 24ECh. 15.7 - Prob. 25ECh. 15.7 - Prob. 26ECh. 15.7 - Prob. 27ECh. 15.7 - Prob. 28ECh. 15.7 - Prob. 29ECh. 15.7 - Prob. 30ECh. 15.7 - Prob. 31ECh. 15.7 - Prob. 32ECh. 15.7 - Prob. 33ECh. 15.7 - Prob. 34ECh. 15.7 - Prob. 35ECh. 15.7 - Prob. 36ECh. 15.7 - Prob. 37ECh. 15.7 - Prob. 38ECh. 15.7 - Prob. 39ECh. 15.7 - Prob. 40ECh. 15.7 - Prob. 41ECh. 15.7 - Prob. 42ECh. 15.7 - Prob. 43ECh. 15.7 - Prob. 44ECh. 15.7 - Prob. 45ECh. 15.7 - Prob. 46ECh. 15.7 - Prob. 47ECh. 15.7 - Prob. 48ECh. 15.7 - Prob. 49ECh. 15.7 - Prob. 50ECh. 15.7 - Prob. 51ECh. 15.7 - Prob. 52ECh. 15.7 - Prob. 53ECh. 15.7 - Prob. 54ECh. 15.7 - Prob. 55ECh. 15.7 - Prob. 56ECh. 15.7 - Prob. 57ECh. 15.7 - Prob. 58ECh. 15.7 - Prob. 59ECh. 15.7 - Prob. 60ECh. 15.7 - Prob. 61ECh. 15.7 - Prob. 62ECh. 15.7 - Prob. 63ECh. 15.7 - Prob. 64ECh. 15.8 - Prob. 1PQCh. 15.8 - Prob. 2PQCh. 15.8 - Prob. 3PQCh. 15.8 - Prob. 1ECh. 15.8 - Prob. 2ECh. 15.8 - Prob. 3ECh. 15.8 - Prob. 4ECh. 15.8 - Prob. 5ECh. 15.8 - Prob. 6ECh. 15.8 - Prob. 7ECh. 15.8 - Prob. 8ECh. 15.8 - Prob. 9ECh. 15.8 - Prob. 10ECh. 15.8 - Prob. 11ECh. 15.8 - Prob. 12ECh. 15.8 - Prob. 13ECh. 15.8 - Prob. 14ECh. 15.8 - Prob. 15ECh. 15.8 - Prob. 16ECh. 15.8 - Prob. 17ECh. 15.8 - Prob. 18ECh. 15.8 - Prob. 19ECh. 15.8 - Prob. 20ECh. 15.8 - Prob. 21ECh. 15.8 - Prob. 22ECh. 15.8 - Prob. 23ECh. 15.8 - Prob. 24ECh. 15.8 - Prob. 25ECh. 15.8 - Prob. 26ECh. 15.8 - Prob. 27ECh. 15.8 - Prob. 28ECh. 15.8 - Prob. 29ECh. 15.8 - Prob. 30ECh. 15.8 - Prob. 31ECh. 15.8 - Prob. 32ECh. 15.8 - Prob. 33ECh. 15.8 - Prob. 34ECh. 15.8 - Prob. 35ECh. 15.8 - Prob. 36ECh. 15.8 - Prob. 37ECh. 15.8 - Prob. 38ECh. 15.8 - Prob. 39ECh. 15.8 - Prob. 40ECh. 15.8 - Prob. 41ECh. 15.8 - Prob. 42ECh. 15.8 - Prob. 43ECh. 15.8 - Prob. 44ECh. 15.8 - Prob. 45ECh. 15.8 - Prob. 46ECh. 15.8 - Prob. 47ECh. 15.8 - Prob. 48ECh. 15.8 - Prob. 49ECh. 15.8 - Prob. 50ECh. 15.8 - Prob. 51ECh. 15.8 - Prob. 52ECh. 15.8 - Prob. 53ECh. 15.8 - Prob. 54ECh. 15.8 - Prob. 55ECh. 15.8 - Prob. 56ECh. 15 - Prob. 1CRECh. 15 - Prob. 2CRECh. 15 - Prob. 3CRECh. 15 - Prob. 4CRECh. 15 - Prob. 5CRECh. 15 - Prob. 6CRECh. 15 - Prob. 7CRECh. 15 - Prob. 8CRECh. 15 - Prob. 9CRECh. 15 - Prob. 10CRECh. 15 - Prob. 11CRECh. 15 - Prob. 12CRECh. 15 - Prob. 13CRECh. 15 - Prob. 14CRECh. 15 - Prob. 15CRECh. 15 - Prob. 16CRECh. 15 - Prob. 17CRECh. 15 - Prob. 18CRECh. 15 - Prob. 19CRECh. 15 - Prob. 20CRECh. 15 - Prob. 21CRECh. 15 - Prob. 22CRECh. 15 - Prob. 23CRECh. 15 - Prob. 24CRECh. 15 - Prob. 25CRECh. 15 - Prob. 26CRECh. 15 - Prob. 27CRECh. 15 - Prob. 28CRECh. 15 - Prob. 29CRECh. 15 - Prob. 30CRECh. 15 - Prob. 31CRECh. 15 - Prob. 32CRECh. 15 - Prob. 33CRECh. 15 - Prob. 34CRECh. 15 - Prob. 35CRECh. 15 - Prob. 36CRECh. 15 - Prob. 37CRECh. 15 - Prob. 38CRECh. 15 - Prob. 39CRECh. 15 - Prob. 40CRECh. 15 - Prob. 41CRECh. 15 - Prob. 42CRECh. 15 - Prob. 43CRECh. 15 - Prob. 44CRECh. 15 - Prob. 45CRECh. 15 - Prob. 46CRECh. 15 - Prob. 47CRECh. 15 - Prob. 48CRECh. 15 - Prob. 49CRECh. 15 - Prob. 50CRECh. 15 - Prob. 51CRECh. 15 - Prob. 52CRECh. 15 - Prob. 53CRECh. 15 - Prob. 54CRECh. 15 - Prob. 55CRECh. 15 - Prob. 56CRECh. 15 - Prob. 57CRECh. 15 - Prob. 58CRECh. 15 - Prob. 59CRECh. 15 - Prob. 60CRECh. 15 - Prob. 61CRECh. 15 - Prob. 62CRECh. 15 - Prob. 63CRE
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Use of ALGEBRA in REAL LIFE; Author: Fast and Easy Maths !;https://www.youtube.com/watch?v=9_PbWFpvkDc;License: Standard YouTube License, CC-BY
Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=P182Abv3fOk;License: Standard YouTube License, CC-BY
Applications of Algebra (Digit, Age, Work, Clock, Mixture and Rate Problems); Author: EngineerProf PH;https://www.youtube.com/watch?v=Y8aJ_wYCS2g;License: Standard YouTube License, CC-BY