
Concept explainers
a.
To calculate: The number of 5-year maturity zeros required to be sold to make the initial cash flow equal to zero, if you buy the one 3 year maturity zero coupon bond.
Introduction:
Initial cash flow: It is supposed to be the amount of money received or paid at the start of a project or investment.
b.
To determine: The cash flows involved in this strategy each year.
Introduction:
Cash flows: It is the total amount of money which comes into the firm or goes out of firm. It mainly affects the liquidity position of the firm.
c.
To calculate: The effective 2-year interest rate on the effective 3-year-ahead forward loan.
Introduction:
Forward mortgage loan: It is one of the fixed-rate mortgages. In this type of loan, the interest rates to be charged ahead can be locked in advance at the start of the mortgage term.
d.
To evaluate: Whether the effective 2-year forward rate is equal to 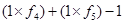 and
and 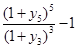
Introduction:
Forward rate of interest: It is supposed to be interest rate related to future period that is confirmed or locked by the parties involved in the financial transaction.
Want to see the full answer?
Check out a sample textbook solution
Chapter 15 Solutions
EBK INVESTMENTS
- What is the future value of $500 invested for 3 years at an annual compound interest rate of 4%?arrow_forwardA loan of $10,000 is taken at an annual interest rate of 6% for 5 years. What is the total interest payable under simple interest? Expalarrow_forwardA loan of $10,000 is taken at an annual interest rate of 6% for 5 years. What is the total interest payable under simple interest?arrow_forward
- You borrow $8,000 at an annual interest rate of 7%, and it compounds yearly for 2 years. What is the total amount payable? Helparrow_forwardYou borrow $8,000 at an annual interest rate of 7%, and it compounds yearly for 2 years. What is the total amount payable?arrow_forwardIf a bond pays $50 annually and is priced at $1,000, what is its annual yield? Explarrow_forward
- If a bond pays $50 annually and is priced at $1,000, what is its annual yield?arrow_forwardA car loan of $15,000 is taken for 3 years at an annual interest rate of 8%. What is the simple interest payable?arrow_forwardYou gave me unhelpful so i am also gave you unhelpful.if you will not give unhelpful then also i will not give unhelpful. what is finance?arrow_forward
- You want to save $15,000 in 5 years. If your bank offers 3% annual interest, how much should you invest today? (Use compound interest.) Explarrow_forwardIf you invest $2,000 at an annual interest rate of 6%, compounded annually, for 3 years, what is the future value?arrow_forwardYou want to save $15,000 in 5 years. If your bank offers 3% annual interest, how much should you invest today? (Use compound interest.)arrow_forward
 Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,
Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,

 Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson,
Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson, Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning
Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education
Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education





