
(a)
The length of diameter of the given sphere.
Answer to Problem 19A
Diameter length of given sphere is
Explanation of Solution
Given information:
A sphere is given whose volume is
Calculation:
As we know that volume of a sphere is given by -
So, diameter length of the sphere will be given as -

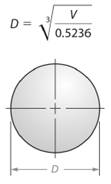
Here, volume of the given sphere is
So, diameter of the sphere will be -
Hence, diameter of given sphere is
(b)
The length of diameter of the given sphere.
Answer to Problem 19A
Diameter length of given sphere is
Explanation of Solution
Given information:
A sphere is given whose volume is
Calculation:
As we know that volume of a sphere is given by -
So, diameter length of the sphere will be given as -

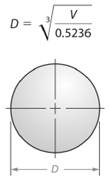
Here, volume of the given sphere is
So, diameter of the sphere will be -
Hence, diameter of given sphere is
(c)
To find the length of diameter of the given sphere.
Answer to Problem 19A
Diameter length of given sphere is
Explanation of Solution
Given information:
A sphere is given whose volume is
Calculation:
As we know that volume of a sphere is given by -
So, diameter length of the sphere will be given as -

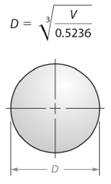
Here, volume of the given sphere is
So, diameter of the sphere will be -
Hence, diameter of given sphere is
(d)
The length of diameter of the given sphere.
Answer to Problem 19A
Diameter length of given sphere is
Explanation of Solution
Given information:
A sphere is given whose volume is
Calculation:
As we know that volume of a sphere is given by -
So, diameter length of the sphere will be given as -

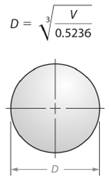
Here, volume of the given sphere is
So, diameter of the sphere will be -
Hence, diameter of given sphere is
(e)
The length of diameter of the given sphere.
Answer to Problem 19A
Diameter length of given sphere is
Explanation of Solution
Given information:
A sphere is given whose volume is
Calculation:
As we know that volume of a sphere is given by -
So, diameter length of the sphere will be given as -

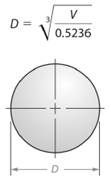
Here, volume of the given sphere is
So, diameter of the sphere will be -
Hence, diameter of given sphere is
Want to see more full solutions like this?
Chapter 15 Solutions
Mathematics For Machine Technology
- 2) Prove that for all integers n > 1. dn 1 (2n)! 1 = dxn 1 - Ꮖ 4 n! (1-x)+/arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
- 3) Let a1, a2, and a3 be arbitrary real numbers, and define an = 3an 13an-2 + An−3 for all integers n ≥ 4. Prove that an = 1 - - - - - 1 - - (n − 1)(n − 2)a3 − (n − 1)(n − 3)a2 + = (n − 2)(n − 3)aı for all integers n > 1.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward1) If f(x) = g¹ (g(x) + a) for some real number a and invertible function g, show that f(x) = (fo fo... 0 f)(x) = g¯¹ (g(x) +na) n times for all integers n ≥ 1.arrow_forwardimage belowarrow_forward
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning





