Chapter 15, Problem 18A

To determine

(a)

The length of radii of the given circle.

Answer to Problem 18A

Radius length of given circle is $4$ inch.

Explanation of Solution

Given information:

A circle is given whose area is

  $50.24$ square inch.

Calculation:

As we know that area of a circle is given by -

  $A=\pi \times R^2$

So, radius length of the circle will be -  $R=\sqrt{\frac{A}{\pi }}$

  

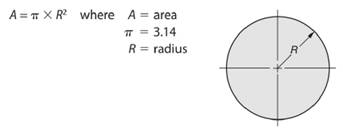
Here, area of the given circle is $50.24$ square inch. i.e. $A=50.24$ square inch.

So, area of the circle will be -

  $\begin{array}{l}R=\sqrt{\frac{A}{\pi }}\\ \Rightarrow R=\sqrt{\frac{50.24}{3.14}\text{ square inch}}\text{ {Put }A=50.24\text{ square inch}}\\ \Rightarrow R=\sqrt{\text{16 square inch}}\\ \Rightarrow R=\sqrt{\text{4 inch }\times \text{ 4 inch}}\\ \Rightarrow R=4\text{ inch}\text{.}\end{array}$

Hence, radius of given circle is $4$ inch.

To determine

(b)

The length of radii of the given circle.

Answer to Problem 18A

Radius length of given circle is $2$ inch.

Explanation of Solution

Given information:

A circle is given whose area is $12.56$ square inch.

Calculation:

As we know that area of a circle is given by -

  $A=\pi \times R^2$

So, radius length of the circle will be -  $R=\sqrt{\frac{A}{\pi }}$

  

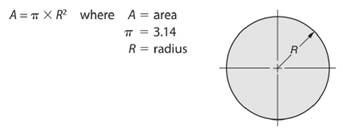
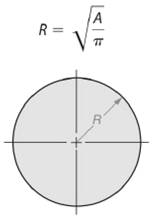
Here, area of the given circle is $12.56$ square inch. i.e. $A=12.56$ square inch.

So, area of the circle will be -

  $\begin{array}{l}R=\sqrt{\frac{A}{\pi }}\\ \Rightarrow R=\sqrt{\frac{12.56}{3.14}\text{ square inch}}\text{ {Put }A=12.56\text{ square inch}}\\ \Rightarrow R=\sqrt{\text{4 square inch}}\\ \Rightarrow R=\sqrt{\text{2 inch }\times \text{ 2 inch}}\\ \Rightarrow R=2\text{ inch}\text{.}\end{array}$

Hence, radius of given circle is $2$ inch.

To determine

(c)

The length of radii of the given circle.

Answer to Problem 18A

Radius length of given circle is $10$ mm.

Explanation of Solution

Given information:

A circle is given whose area is $314$ square mm.

Calculation:

As we know that area of a circle is given by -

  $A=\pi \times R^2$

So, radius length of the circle will be -  $R=\sqrt{\frac{A}{\pi }}$

  

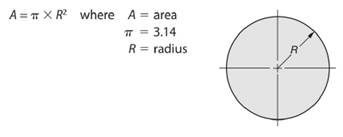
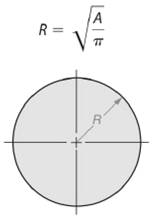
Here, area of the given circle is $314$ square mm. i.e. $A=314$ square mm.

So, area of the circle will be -

  $\begin{array}{l}R=\sqrt{\frac{A}{\pi }}\\ \Rightarrow R=\sqrt{\frac{314}{3.14}\text{ square mm}}\text{ {Put }A=314\text{ square mm}}\\ \Rightarrow R=\sqrt{\text{100 square mm}}\\ \Rightarrow R=\sqrt{\text{10 mm }\times \text{ 10 mm}}\\ \Rightarrow R=10\text{ mm}\text{.}\end{array}$

Hence, radius of given circle is $10$ mm.

To determine

(d)

To workout the length of radii of the given circle.

Answer to Problem 18A

Radius length of given circle is $3$ inch.

Explanation of Solution

Given information:

A circle is given whose area is $28.26$ square inch.

Calculation:

As we know that area of a circle is given by -

  $A=\pi \times R^2$

So, radius length of the circle will be -  $R=\sqrt{\frac{A}{\pi }}$

  

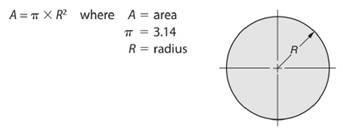
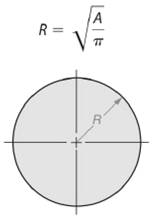
Here, area of the given circle is $28.26$ square inch. i.e. $A=28.26$ square inch.

So, area of the circle will be -

  $\begin{array}{l}R=\sqrt{\frac{A}{\pi }}\\ \Rightarrow R=\sqrt{\frac{28.26}{3.14}\text{ square inch}}\text{ {Put }A=28.26\text{ square inch}}\\ \Rightarrow R=\sqrt{\text{9 square inch}}\\ \Rightarrow R=\sqrt{\text{3 inch }\times \text{ 3 inch}}\\ \Rightarrow R=3\text{ inch}\text{.}\end{array}$

Hence, radius of given circle is $3$ inch.

To determine

(e)

The length of radii of the given circle.

Answer to Problem 18A

Radius length of given circle is $7$ mm.

Explanation of Solution

Given information:

A circle is given whose area is $153.86$ square mm.

Calculation:

As we know that area of a circle is given by -

  $A=\pi \times R^2$

So, radius length of the circle will be -  $R=\sqrt{\frac{A}{\pi }}$

  

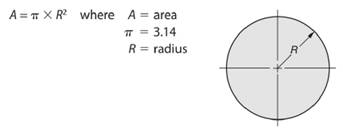
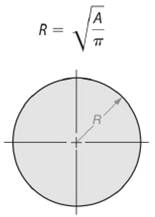
Here, area of the given circle is $153.86$ square mm. i.e. $A=153.86$ square mm.

So, area of the circle will be -

  $\begin{array}{l}R=\sqrt{\frac{A}{\pi }}\\ \Rightarrow R=\sqrt{\frac{153.86}{3.14}\text{ square mm}}\text{ {Put }A=153.86\text{square mm}}\\ \Rightarrow R=\sqrt{\text{49 square mm}}\\ \Rightarrow R=\sqrt{\text{7 mm }\times \text{ 7 mm}}\\ \Rightarrow R=7\text{ mm}\text{.}\end{array}$

Hence, radius of given circle is $7$ mm.