EBK PHYSICS FOR SCIENTISTS AND ENGINEER
9th Edition
ISBN: 9780100460300
Author: SERWAY
Publisher: YUZU
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
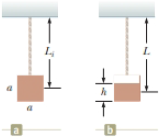
Chapter 15, Problem 15.89CP
A light, cubical container of volume a3 is initially filled with a liquid of mass density ρ as shown in Figure P15.5la. The cube is initially supported by a light string to form a simple pendulum of length Li, measured from the center of mass of the filled container, where Li>> a. The liquid is allowed to flow from the bottom of the container at a constant rate (dM/dt). At any time t, the level of the liquid in the container is h and the length of the pendulum is L. (measured relative to the instantaneous center of mass) as shown in Figure P15.51b. (a) Find the period of the pendulum as a function of time. (b) What is the period of the pendulum after the liquid completely runs out of the container?
Figure P15.51
Expert Solution & Answer
Trending nowThis is a popular solution!
Chapter 15 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
Ch. 15 - A block on the end of a spring is pulled to...Ch. 15 - Consider a graphical representation (Fig. 15.3) of...Ch. 15 - Figure 15.4 shows two curves representing...Ch. 15 - An object of mass m is hung from a spring and set...Ch. 15 - The ball in Figure 15.13 moves in a circle of...Ch. 15 - The grandfather clock in the opening storyline...Ch. 15 - If a simple pendulum oscillates with small...Ch. 15 - You attach a block to the bottom end of a spring...Ch. 15 - A block-spring system vibrating on a frictionless,...Ch. 15 - An object-spring system moving with simple...
Ch. 15 - An object of mass 0.40 kg, hanging from a spring...Ch. 15 - A runaway railroad car, with mass 3.0 105 kg,...Ch. 15 - The position of an object moving with simple...Ch. 15 - If an object of mass m attached to a light spring...Ch. 15 - You stand on the end of a diving board and bounce...Ch. 15 - A mass-spring system moves with simple harmonic...Ch. 15 - A block with mass m = 0.1 kg oscillates with...Ch. 15 - For a simple harmonic oscillator, answer yes or no...Ch. 15 - The top end of a spring is held fixed. A block is...Ch. 15 - Which of the following statements is not true...Ch. 15 - A simple pendulum has a period of 2.5 s. (i) What...Ch. 15 - A simple pendulum is suspended from the ceiling of...Ch. 15 - A particle on a spring moves in simple harmonic...Ch. 15 - You are looking at a small, leafy tree. You do not...Ch. 15 - Prob. 15.2CQCh. 15 - If the coordinate of a particle varies as x = -A...Ch. 15 - A pendulum bob is made from a sphere filled with...Ch. 15 - Figure CQ15.5 shows graphs of the potential energy...Ch. 15 - A student thinks that any real vibration must be...Ch. 15 - The mechanical energy of an undamped block-spring...Ch. 15 - Is it possible to have damped oscillations when a...Ch. 15 - Will damped oscillations occur for any values of b...Ch. 15 - If a pendulum clock keeps perfect time al the base...Ch. 15 - Prob. 15.11CQCh. 15 - A simple pendulum can be modeled as exhibiting...Ch. 15 - Consider the simplified single-piston engine in...Ch. 15 - A 0.60-kg block attached to a spring with force...Ch. 15 - When a 4.25-kg object is placed on lop of a...Ch. 15 - A vertical spring stretches 3.9 cm when a 10-g...Ch. 15 - In an engine, a piston oscillates with simpler...Ch. 15 - The position of a particle is given by the...Ch. 15 - A piston in a gasoline engine is in simple...Ch. 15 - A 1.00-kg object is attached to a horizontal...Ch. 15 - A simple harmonic oscillator takes 12.0 s to...Ch. 15 - A 7.00-kg object is hung from the bottom end of a...Ch. 15 - At an outdoor market, a bunch of bananas attached...Ch. 15 - A vibration sensor, used in testing a washing...Ch. 15 - (a) A hanging spring stretches by 35.0 cm when an...Ch. 15 - Review. A particle moves along the x axis. It is...Ch. 15 - A ball dropped from a height of 4.00 m makes an...Ch. 15 - A particle moving along the x axis in simple...Ch. 15 - The initial position, velocity, and acceleration...Ch. 15 - A particle moves in simple harmonic motion with a...Ch. 15 - A 1.00-kg glider attached to a spring with a force...Ch. 15 - A 0.500-kg object attached to a spring with a...Ch. 15 - You attach an object to the bottom end of a...Ch. 15 - To test the resiliency of its bumper during...Ch. 15 - A 200-g block is attached to a horizontal spring...Ch. 15 - A block of unknown mass is attached to a spring...Ch. 15 - A block-spring system oscillates with an amplitude...Ch. 15 - A particle executes simple harmonic motion with an...Ch. 15 - The amplitude of a system moving in simple...Ch. 15 - A 50.0-g object connected to a spring with a force...Ch. 15 - A 2.00-kg object is attached to a spring and...Ch. 15 - A simple harmonic oscillator of amplitude A has a...Ch. 15 - Review. A 65.0-kg bungee jumper steps off a bridge...Ch. 15 - Review. A 0.250-kg block resting on a...Ch. 15 - Prob. 15.32PCh. 15 - While driving behind a car traveling at 3.00 m/s,...Ch. 15 - A seconds pendulum is one that moves through its...Ch. 15 - A simple pendulum makes 120 complete oscillations...Ch. 15 - A particle of mass m slides without friction...Ch. 15 - A physical pendulum in the form of a planar object...Ch. 15 - A physical pendulum in the form of a planar object...Ch. 15 - The angular position of a pendulum is represented...Ch. 15 - Consider the physical pendulum of Figure 15.16....Ch. 15 - Prob. 15.41PCh. 15 - A very light rigid rod of length 0.500 m extends...Ch. 15 - Review. A simple pendulum is 5.00 m long. What is...Ch. 15 - A small object is attached to the end of a string...Ch. 15 - A watch balance wheel (Fig. P15.25) has a period...Ch. 15 - A pendulum with a length of 1.00 m is released...Ch. 15 - A 10.6-kg object oscillates at the end of a...Ch. 15 - Show that the time rate of change of mechanical...Ch. 15 - Show that Equation 15.32 is a solution of Equation...Ch. 15 - A baby bounces up and down in her crib. Her mass...Ch. 15 - As you enter a fine restaurant, you realize that...Ch. 15 - A block weighing 40.0 N is suspended from a spring...Ch. 15 - A 2.00-kg object attached to a spring moves...Ch. 15 - Considering an undamped, forced oscillator (b =...Ch. 15 - Damping is negligible for a 0.150-kg object...Ch. 15 - The mass of the deuterium molecule (D2) is twice...Ch. 15 - An object of mass m moves in simple harmonic...Ch. 15 - Review. This problem extends the reasoning of...Ch. 15 - A small ball of mass M is attached to the end of a...Ch. 15 - Review. A rock rests on a concrete sidewalk. An...Ch. 15 - Four people, each with a mass of 72.4 kg, are in a...Ch. 15 - To account for the walking speed of a bipedal or...Ch. 15 - Prob. 15.63APCh. 15 - An object attached to a spring vibrates with...Ch. 15 - Review. A large block P attached to a light spring...Ch. 15 - Review. A large block P attached to a light spring...Ch. 15 - A pendulum of length L and mass M has a spring of...Ch. 15 - A block of mass m is connected to two springs of...Ch. 15 - A horizontal plank of mass 5.00 kg and length 2.00...Ch. 15 - A horizontal plank of mass m and length L is...Ch. 15 - Review. A particle of mass 4.00 kg is attached to...Ch. 15 - A ball of mass m is connected to two rubber bands...Ch. 15 - Review. One end of a light spring with force...Ch. 15 - People who ride motorcycles and bicycles learn to...Ch. 15 - A simple pendulum with a length of 2.23 m and a...Ch. 15 - When a block of mass M, connected to the end of a...Ch. 15 - Review. A light balloon filled with helium of...Ch. 15 - Consider the damped oscillator illustrated in...Ch. 15 - A particle with a mass of 0.500 kg is attached to...Ch. 15 - Your thumb squeaks on a plate you have just...Ch. 15 - Review. A lobstermans buoy is a solid wooden...Ch. 15 - Prob. 15.82APCh. 15 - Two identical steel balls, each of mass 67.4 g,...Ch. 15 - A smaller disk of radius r and mass m is attached...Ch. 15 - An object of mass m1 = 9.00 kg is in equilibrium...Ch. 15 - Review. Why is the following situation impassible?...Ch. 15 - A block of mass M is connected to a spring of mass...Ch. 15 - Review. A system consists of a spring with force...Ch. 15 - A light, cubical container of volume a3 is...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Explain what happens to the energy carried by light that it is dimmed by passing it through two crossed polariz...
College Physics
Is Earths inner core solid and the outer core liquid because the inner core is cooler than the outer core? Expl...
Conceptual Integrated Science
1. Rub your hands together vigorously. What happens? Discuss the energy transfers and transformations that take...
College Physics: A Strategic Approach (4th Edition)
1.19 [I] An ant walked 10.0 cm across the floor in 6.2 s. What was its average speed in m/s?
[Hint: 2 signi...
Schaum's Outline of College Physics, Twelfth Edition (Schaum's Outlines)
60. The solar system is 25,000 light years from the center of our Milky Way galaxy. One light year is the dista...
Physics for Scientists and Engineers: A Strategic Approach with Modern Physics (4th Edition)
The net force between the thymine and adenine.
Physics: Principles with Applications
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A manometer containing water with one end connected to a container of gas has a column height difference of 0.60 m (Fig. P15.72). If the atmospheric pressure on the right column is 1.01 105 Pa, find the absolute pressure of the gas in the container. The density of water is 1.0 103 kg/m3. FIGURE P15.72arrow_forwardA hollow copper (Cu = 8.92 103 kg/m3) spherical shell of mass m = 0.950 kg floats on water with its entire volume below the surface. a. What is the radius of the sphere? b. What is the thickness of the shell wall?arrow_forwardWater is flowing through a pipe that has a constriction opening into a region with a wider cross-sectional area. If the pipe regions are cylindrical with radii of 0.10 m and 0.35 m, respectively, and the water is moving with a speed of 1.50 m/s in the wider section, what is the speed of the water in the constricted section?arrow_forward
- A manometer is shown in Figure P15.36. Rank the pressures at the five locations indicated from highest to lowest. Indicate equal pressures, if any. FIGURE P15.36arrow_forward(a) How high will water rise in a glass capillary tube with a 0.500-mm radius? (b) How much gravitational potential energy does the water gain? (c) Discuss possible sources of this energy.arrow_forward(a) A water hose 2.00 cm in diameter is used to fill a 20.0-L bucket. If it takes 1.00 min to fill the bucket, what is the speed v at which water moves through the hose? (Note: 1 L = 1 000 cm3.) (b) The hose has a nozzle 1.00 cm in diameter. Find the speed of the water at the nozzle.arrow_forward
- Review. In a water pistol, a piston drives water through a large tube of area A1 into a smaller tube of area A2 as shown in Figure P14.46. The radius of the large tube is 1.00 cm and that of the small tube is 1.00 mm. The smaller tube is 3.00 cm above the larger tube. (a) If the pistol is fired horizontally at a height of 1.50 m, determine the time interval required for the water to travel from the nozzle to the ground. Neglect air resistance and assume atmospheric pressure is 1.00 atm. (b) If the desired range of the stream is 8.00 m, with what speed v2 must the stream leave the nozzle? (c) At what speed v1 must the plunger be moved to achieve the desired range? (d) What is the pressure at the nozzle? (e) Find the pressure needed in the larger tube. (f) Calculate the force that must be exerted on the trigger to achieve the desired range. (The force that must be exerted is due to pressure over and above atmospheric pressure.) Figure P14.46arrow_forwardA fluid flows through a horizontal pipe that widens, making a 45 angle with the y axis (Fig. P15.48). The thin part of the pipe has radius R, and the fluids speed in the thin part of the pipe is v0. The origin of the coordinate system is at the point where the pipe begins to widen. The pipes cross section is circular. a. Find an expression for the speed v(x) of the fluid as a function of position for x 0 b. Plot your result: v(x) versus x. FIGURE P15.48 (a) The continuity equation (Eq. 15.21) relates the cross-sectional area to the speed of the fluid traveling through the pipe. A0v0 = A(x)v(x) v(x)=A0v0A(x) The cross sectional area is the area of a circle whose radius is y(x). The widening pan of the pipe is a straight line with slope of 1 and intercept y(0) = R. y(x) = mx + b = x + R A(x) = [y(x)]2 = (x + R)2 Plug this into the formula for the velocity. Plug this into the formula for the velocity. v(x)=A0v0(x+R)2arrow_forwardTo allow a car to slow down or stop, hydraulic brakes transmit forces from a master cylinder to the brake pads through a fluid. Imagine this system as a tube filled with an incompressible fluid and a piston on each end. A force of 95.0 N is applied to a piston 2.65 cm in diameter on one end of the tube. a. What is the magnitude of the force that is exerted on the piston 5.15 cm in diameter on the other side? b. If the 2.65-cm piston is displaced by 1.00 cm, by how much is the 5.15-cm piston displaced?arrow_forward
- A rectangular block of Styrofoam 25.0 cm in length, 15.0 cm in width, and 12.0 cm in height is placed in a large tub of water. Assume the density of Styrofoam is 3.00 102 kg/m3. a. What volume of the block is submerged? b. A copper block is now placed atop the Styrofoam block so that the top of the Styrofoam block is level with the surface of the water. What is the mass of the copper block?arrow_forwardA 10.0-kg block of metal measuring 12.0 cm by 10.0 cm by 10.0 cm is suspended from a scale and immersed in water as shown in Figure P15.24b. The 12.0-cm dimension is vertical, and the top of the block is 5.00 cm below the surface of the water. (a) What are the magnitudes of the forces acting on the top and on the bottom of the block due to the surrounding water? (b) What is the reading of the spring scale? (c) Show that the buoyant force equals the difference between the forces at the top and bottom of the block.arrow_forwardA uniform wooden board of length L and mass M is hinged at the top of a vertical wall of a container partially filled with a certain liquid (Fig. P15.81). (If there were no liquid in the container, the board would hang straight down.) Three-fifths of the length of the board is submerged in the liquid when the board is in equilibrium. Find the ratio of the densities of the liquid and the board.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Fluids in Motion: Crash Course Physics #15; Author: Crash Course;https://www.youtube.com/watch?v=fJefjG3xhW0;License: Standard YouTube License, CC-BY