
Concept explainers
A smaller disk of radius r and mass m is attached rigidly to the face of a second larger disk of radius R and mass M as shown in Figure P15.48. The center of the small disk is located at the edge of the large disk. The large disk is mounted at its center on a frictionless axle. The assembly is rotated through a small angle θ from its equilibrium position and released. (a) Show that the speed of the center of the small disk as it passes through the equilibrium position is
(b) Show that the period of the motion is
Figure P15.48
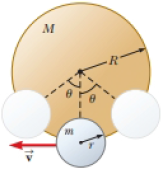
(a)
The speed of the center of the small disk as it passes through the equilibrium position is
Answer to Problem 15.84CP
The speed of the center of the small disk as it passes through the equilibrium position is
Explanation of Solution
The radius of the smaller disk is
Consider the figure for the given situation.

Figure (1)
The loss in the potential energy at
Write the expression for the height of the smaller disk from the centre point
Here,
Substitute
Here,
Write the expression for the loss in potential energy.
Here,
Substitute
Write the expression for the moment of inertia of the larger disk about the cylinder axis.
Here,
Write the expression for the moment of inertia of the smaller disk about the cylinder axis.
Here,
Write the expression for the moment of inertia of the smaller disk about the diameter.
Here,
Write the expression for the net moment of inertia of the two disk system.
Here,
Substitute
Write the expression for the angular velocity of the disk.
Here,
The gain in kinetic energy of the system is equal to the sum of the center of mass of the small disk, the rotational energy of the larger disk and the rotational energy of the smaller disk about
Write the expression for the gain in kinetic energy of the system.
Here,
Substitute
Apply conservation law of energy.
Substitute
Further solve the above equation.
Conclusion:
Therefore, the speed of the center of the small disk as it passes through the equilibrium position is
(b)
The period of the motion is
Answer to Problem 15.84CP
The period of the motion is
Explanation of Solution
As the value of angle at which assembly is rotated is very small.
From the figure, write the expression for the equation of motion.
Substitute
Write the expression for the equation of motion.
Compare equations (1) and (2).
Formula to calculate the period of the motion is,
Here,
Substitute
Substitute
Conclusion:
Therefore, the period of the motion is
Want to see more full solutions like this?
Chapter 15 Solutions
PHYSICS 1250 PACKAGE >CI<
Additional Science Textbook Solutions
Tutorials in Introductory Physics
Conceptual Physical Science Explorations
Schaum's Outline of College Physics, Twelfth Edition (Schaum's Outlines)
University Physics Volume 3
Introduction To Health Physics
Introduction to Electrodynamics
- The puck in Figure P11.46 has a mass of 0.120 kg. The distance of the puck from the center of rotation is originally 40.0 cm, and the puck is sliding with a speed of 80.0 cm/s. The string is pulled downward 15.0 cm through the hole in the frictionless table. Determine the work done on the puck. (Suggestion: Consider the change of kinetic energy.) Figure P11.46arrow_forwardThe angular momentum vector of a precessing gyroscope sweeps out a cone as shown in Figure P11.31. The angular speed of the tip of the angular momentum vector, called its precessional frequency, is given by p=/I, where is the magnitude of the torque on the gyroscope and L is the magnitude of its angular momentum. In the motion called precession of the equinoxes, the Earths axis of rotation processes about the perpendicular to its orbital plane with a period of 2.58 104 yr. Model the Earth as a uniform sphere and calculate the torque on the Earth that is causing this precession. Figure P11.31 A precessing angular momentum vector sweeps out a cone in space.arrow_forwardFigure P10.16 shows the drive train of a bicycle that has wheels 67.3 cm in diameter and pedal cranks 17.5 cm long. The cyclist pedals at a steady cadence of 76.0 rev/min. The chain engages with a front sprocket 15.2 cm in diameter and a rear sprocket 7.00 cm in diameter. Calculate (a) the speed of a link of the chain relative to the bicycle frame, (b) the angular speed of the bicycle wheels, and (c) the speed of the bicycle relative to the road. (d) What pieces of data, if any, are not necessary for the calculations? Figure P10.16arrow_forward
- Figure OQ10.8 shows a system of four particles joined by light, rigid rods. Assume a = b and M is larger than m. About which of the coordinate axes does the system have (i) the smallest and (ii) the largest moment of inertia? (a) the x axis (b) the y axis (c) the z axis. (d) The moment of inertia has the same small value for two axes. (e) The moment of inertia is the same for all three axes. Figure OQ10.8arrow_forwardA tennis ball is a hollow sphere with a thin wall. It is set rolling without slipping at 4.03 m/s on a horizontal section of a track as shown in Figure P10.62. It rolls around the inside of a vertical circular loop of radius r = 45.0 cm. As the ball nears the bottom of the loop, the shape of the track deviates from a perfect circle so that the ball leaves the track at a point h = 20.0 cm below the horizontal section. (a) Find the balls speed at the top of the loop. (b) Demonstrate that the ball will not fall from the track at the top of the loop. (c) Find the balls speed as it leaves the track at the bottom. What If? (d) Suppose that static friction between ball and track were negligible so that the ball slid instead of rolling. Would its speed then be higher, lower, or the same at the top of the loop? (e) Explain your answer to part (d). Figure P10.62arrow_forwardA space probe is fired as a projectile from the Earths surface with an initial speed of 2.00 104 m/s. What will its speed be when it is very far from the Earth? Ignore atmospheric friction and the rotation of the Earth. P11.26 Ki+Ui=Kf+Uf12mvi2+GMEm(1rf1ri)=12mvf212vi2+GME(01RE)=12vf2orvf2=v122GMEREandvf=(v122GMERE)1/2,vf=[(2.00104)21.25108]1/2m/s=1.66104m/sarrow_forward
- A wad of sticky clay with mass m and velocity vi is fired at a solid cylinder of mass M and radius R (Fig. P10.75). The cylinder is initially at rest and is mounted on a fixed horizontal axle that runs through its center of mass. The line of motion of the projectile is perpendicular to the axle and at a distance d R from the center. (a) Find the angular speed of the system just after the clay strikes and sticks to the surface of the cylinder. (b) Is the mechanical energy of the claycylinder system constant in this process? Explain your answer. (c) Is the momentum of the claycylinder system constant in this process? Explain your answer. Figure P10.75arrow_forwardA uniform solid sphere of mass m and radius r is releasedfrom rest and rolls without slipping on a semicircular ramp ofradius R r (Fig. P13.76). Ifthe initial position of the sphereis at an angle to the vertical,what is its speed at the bottomof the ramp? FIGURE P13.76arrow_forwardA projectile of mass m moves to the right with a speed vi (Fig. P10.81a). The projectile strikes and sticks to the end of a stationary rod of mass M, length d, pivoted about a frictionless axle perpendicular to the page through O (Fig. P10.81b). We wish to find the fractional change of kinetic energy in the system due to the collision. (a) What is the appropriate analysis model to describe the projectile and the rod? (b) What is the angular momentum of the system before the collision about an axis through O? (c) What is the moment of inertia of the system about an axis through O after the projectile sticks to the rod? (d) If the angular speed of the system after the collision is , what is the angular momentum of the system after the collision? (e) Find the angular speed after the collision in terms of the given quantities. (f) What is the kinetic energy of the system before the collision? (g) What is the kinetic energy of the system after the collision? (h) Determine the fractional change of kinetic energy due to the collision. Figure P10.81arrow_forward
- Two astronauts (Fig. P10.67), each having a mass M, are connected by a rope of length d having negligible mass. They are isolated in space, orbiting their center of mass at speeds v. Treating the astronauts as particles, calculate (a) the magnitude of the angular momentum of the two-astronaut system and (b) the rotational energy of the system. By pulling on the rope, one of the astronauts shortens the distance between them to d/2. (c) What is the new angular momentum of the system? (d) What are the astronauts new speeds? (e) What is the new rotational energy of the system? (f) How much chemical potential energy in the body of the astronaut was converted to mechanical energy in the system when he shortened the rope? Figure P10.67 Problems 67 and 68.arrow_forwardConsider the disk in Problem 71. The disks outer rim hasradius R = 4.20 m, and F1 = 10.5 N. Find the magnitude ofeach torque exerted around the center of the disk. FIGURE P12.71 Problems 71-75arrow_forwardTwo particles of mass m1 = 2.00 kgand m2 = 5.00 kg are joined by a uniform massless rod of length = 2.00 m(Fig. P13.48). The system rotates in thexy plane about an axis through the midpoint of the rod in such a way that theparticles are moving with a speed of 3.00 m/s. What is the angular momentum of the system? FIGURE P13.48arrow_forward
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning





