CALCULUS EARLY TRANSCENDENTALS W/ WILE
CALCULUS EARLY TRANSCENDENTALS W/ WILE
11th Edition
ISBN: 9781119228509
Author: Anton
Publisher: WILEY
bartleby

Videos

Textbook Question
Book Icon
Chapter 14.7, Problem 34ES

Find a transformation u = f x ,   y ,   υ = g x ,   y that when applied to the region R in the xy-plane has as its image the region S in the u υ -plane .

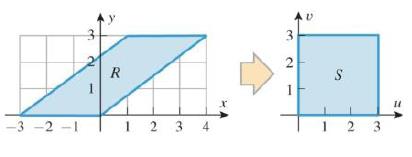
Chapter 14.7, Problem 34ES, Find a transformation u=fx,y,=gx,y that when applied to the region R in the xy-plane has as its

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 14.7, Problem 33ES
Next
Chapter 14.7, Problem 35ES
Students have asked these similar questions
9. Let R be a square with vertices (0,0), (1,1), (2,0) and (1, -1) in the xy-plane. It might be useful/helpful to sketch the region R and the region S a) Find the image Sin the uv-plane under the transformation T: x=u + v, y = u - V hint: solve for u by solving for x + y (use system) b)Write the Jacobian Matrix of partial derivatives c) evaluate the determinant of the Jacobian d) Rewrite the integral using a change of variables to u and v with the Jacobian and evaluate the new integral. SSR xydA
Evaluate the circulation of G = xyi + zj + 4yk around a square of side 4, centered at the origin, lying in the yz-plane, and oriented counterclockwise when viewed from the positive x-axis. Circulation = Jo F. dr =
Evaluate exp{}dA where R is the region in the ry-plane bounded by the trapezoid with vertices (0, 1), (0, 2), (2,0), and (1,0) by a suitable change of variables.

Chapter 14 Solutions

CALCULUS EARLY TRANSCENDENTALS W/ WILE

Ch. 14.1 - Prob. 1QCECh. 14.1 - The iterated integral 1524fx,ydxdy integrates f...Ch. 14.1 - Supply the missing integrand and limits of...Ch. 14.1 - Prob. 4QCECh. 14.1 - Evaluate the iterated integrals. 0102x+3dydxCh. 14.1 - Evaluate the iterated integrals. 13112x4ydydxCh. 14.1 - Evaluate the iterated integrals. 2401x2ydxdyCh. 14.1 - Evaluate the iterated integrals. 2012x2+y2dxdyCh. 14.1 - Evaluate the iterated integrals. 0ln30ln2ex+ydydxCh. 14.1 - Evaluate the iterated integrals. 0201ysinxdydx
Ch. 14.1 - Evaluate the iterated integrals. 1025dxdyCh. 14.1 - Evaluate the iterated integrals. 4637dydxCh. 14.1 - Evaluate the iterated integrals. 0101xxy+12dydxCh. 14.1 - Evaluate the iterated integrals. /212xcosxydydxCh. 14.1 - Evaluate the iterated integrals. 0ln201xyey2xdydxCh. 14.1 - Evaluate the iterated integrals. 34121x+y2dydxCh. 14.1 - Evaluate the double integral over the rectangular...Ch. 14.1 - Evaluate the double integral over the rectangular...Ch. 14.1 - Evaluate the double integral over the rectangular...Ch. 14.1 - Evaluate the double integral over the rectangular...Ch. 14.1 - (a) Let fx,y=x2+y, and as shown in the...Ch. 14.1 - (a) Let fx,y=x2y, and as shown in Exercise 17, let...Ch. 14.1 - Each iterated integral represents the volume of a...Ch. 14.1 - Each iterated integral represents the volume of a...Ch. 14.1 - Each iterated integral represents the volume of a...Ch. 14.1 - Each iterated integral represents the volume of a...Ch. 14.1 - Determine whether the statement is true or false....Ch. 14.1 - Determine whether the statement is true or false....Ch. 14.1 - Determine whether the statement is true or false....Ch. 14.1 - Determine whether the statement is true or false....Ch. 14.1 - In this exercise, suppose that fx,y=gxhy and...Ch. 14.1 - Use the result in Exercise 27 to evaluate the...Ch. 14.1 - Use a double integral to find the volume. The...Ch. 14.1 - Use a double integral to find the volume. The...Ch. 14.1 - Use a double integral to find the volume. The...Ch. 14.1 - Use a double integral to find the volume. The...Ch. 14.1 - Evaluate the integral by choosing a convenient...Ch. 14.1 - (a) Sketch the solid in the first octant that is...Ch. 14.1 - The average value or mean value of a continuous...Ch. 14.1 - The average value or mean value of a continuous...Ch. 14.1 - The average value or mean value of a continuous...Ch. 14.1 - The average value or mean value of a continuous...Ch. 14.1 - The average value or mean value of a continuous...Ch. 14.1 - The average value or mean value of a continuous...Ch. 14.1 - Use a CAS to evaluate the iterated integrals...Ch. 14.1 - Use a CAS to show that the volume V under the...Ch. 14.1 - Discuss how computing a volume using an iterated...Ch. 14.1 - Discuss how the double integral property given in...Ch. 14.2 - Supply the missing integrand and limits of...Ch. 14.2 - Let R be the triangular region in the xyplane with...Ch. 14.2 - Let R be the triangular region in xy-plane with...Ch. 14.2 - The line and the parabola intersect at the...Ch. 14.2 - Evaluate the iterated integral. 01x2xxy2dydxCh. 14.2 - Evaluate the iterated integral. 13/2y3yydxdyCh. 14.2 - Evaluate the iterated integral. 0309y2ydxdyCh. 14.2 - Evaluate the iterated integral. 1/41x2xxydydxCh. 14.2 - Evaluate the iterated integral. Ch. 14.2 - Evaluate the iterated integral. Ch. 14.2 - Evaluate the iterated integral. Ch. 14.2 - Evaluate the iterated integral. 120y2ex/y2dxdyCh. 14.2 - Let R be the region shown in the accompanying...Ch. 14.2 - Let R be the region shown in the accompanying...Ch. 14.2 - Let R be the region shown in the accompanying...Ch. 14.2 - Let R be the region shown in the accompanying...Ch. 14.2 - Evaluate RxydA, where R is the region in (a)...Ch. 14.2 - Evaluate R(x+y)dA, where R is the region in (a)...Ch. 14.2 - Evaluate the double integral in two ways using...Ch. 14.2 - Evaluate the double integral in two ways using...Ch. 14.2 - Evaluate the double integral in two ways using...Ch. 14.2 - Evaluate the double integral in two ways using...Ch. 14.2 - Evaluate the double integral. Rx(1+y2)1/2dA; R is...Ch. 14.2 - Evaluate the double integral. RxcosydA;R is the...Ch. 14.2 - Evaluate the double integral. RxydA;R is the...Ch. 14.2 - Evaluate the double integral. RxdA:R is the region...Ch. 14.2 - Evaluate the double integral. R(x1)dA;R is the...Ch. 14.2 - Evaluate the double integral. is the region in...Ch. 14.2 - Evaluate where R is the region bounded by Ch. 14.2 - Evaluate where R is the region bounded by Ch. 14.2 - (a) By hand or with the help of a graphing...Ch. 14.2 - (a) By hand or with the help of a graphing...Ch. 14.2 - Use double integration to find the area of the...Ch. 14.2 - Use double integration to find the area of the...Ch. 14.2 - Use double integration to find the area of the...Ch. 14.2 - Use double integration to find the area of the...Ch. 14.2 - Determine whether the statement is true or false....Ch. 14.2 - Determine the statement is true or false. Explain...Ch. 14.2 - Determine whether the statement is true or false....Ch. 14.2 - Determine whether the statement is true or false....Ch. 14.2 - Use double integration to find the volume of the...Ch. 14.2 - Use double integration to find the volume of the...Ch. 14.2 - Use double integration to find the volume of each...Ch. 14.2 - Use double integration to find the volume of each...Ch. 14.2 - Use double integration to find the volume of each...Ch. 14.2 - Use double integration to find the volume of each...Ch. 14.2 - Use double integration to find the volume of each...Ch. 14.2 - Use double integration to find the volume of each...Ch. 14.2 - Use a double integral and a CAS to find the volume...Ch. 14.2 - Use a double integral and a CAS to find the volume...Ch. 14.2 - Express the integral as an equivalent integral...Ch. 14.2 - Express the integral as an equivalent integral...Ch. 14.2 - Express the integral as an equivalent integral...Ch. 14.2 - Express the integral as an equivalent integral...Ch. 14.2 - Express the integral as an equivalent integral...Ch. 14.2 - Express the integral as an equivalent integral...Ch. 14.2 - Evaluate the integral by first reversing the order...Ch. 14.2 - Evaluate the integral by first reversing the order...Ch. 14.2 - Evaluate the integral by first reversing the order...Ch. 14.2 - Evaluate the integral by first reversing the order...Ch. 14.2 - Try to evaluate the integral with a CAS using the...Ch. 14.2 - Use the appropriate Wallis formula (see Exercise...Ch. 14.2 - Evaluate Rxy2dA over the region R shown in the...Ch. 14.2 - Give a geometric argument to show that...Ch. 14.2 - The average value or mean value of a continuous...Ch. 14.2 - The average value or mean value of a continuous...Ch. 14.2 - Prob. 63ESCh. 14.2 - A circular lens of radius 2 inches has thickness...Ch. 14.2 - Use a CAS to approximate the intersections of the...Ch. 14.3 - The polar region inside the circle and outside...Ch. 14.3 - Let R be the region in the first quadrant enclosed...Ch. 14.3 - Let V be the volume of the solid bounded above by...Ch. 14.3 - Express the iterated integral as a double integral...Ch. 14.3 - Evaluate the iterated integral. 0/20sinrcosdrdCh. 14.3 - Evaluate the iterated integral. 001+cosrdrdCh. 14.3 - Evaluate the iterated integral. 0/20asinr2drdCh. 14.3 - Evaluate the iterated integral. 0/60cos3rdrdCh. 14.3 - Evaluate the iterated integral. 001sinr2cosdrdCh. 14.3 - Evaluate the iterated integral. 0/20cosr3drdCh. 14.3 - Use a double integral in polar coordinates to find...Ch. 14.3 - Use a double integral in polar coordinates to find...Ch. 14.3 - Use a double integral in polar coordinates to find...Ch. 14.3 - Use a double integral in polar coordinates to find...Ch. 14.3 - Let R be the region described. Sketch the region R...Ch. 14.3 - Let R be the region described. Sketch the region R...Ch. 14.3 - Express the volume of the solid described as a...Ch. 14.3 - Express the volume of the solid described as a...Ch. 14.3 - Express the volume of the solid described as a...Ch. 14.3 - Express the volume of the solid described as a...Ch. 14.3 - Find the volume of the solid described in the...Ch. 14.3 - Find the volume of the solid described in the...Ch. 14.3 - Find the volume of the solid described in the...Ch. 14.3 - Find the volume of the solid described in the...Ch. 14.3 - Find the volume of the solid in the first octant...Ch. 14.3 - Find the volume of the solid inside the surface...Ch. 14.3 - Use polar coordinates to evaluate the double...Ch. 14.3 - Use polar coordinates to evaluate the double...Ch. 14.3 - Use polar coordinates to evaluate the double...Ch. 14.3 - Use polar coordinates to evaluate the double...Ch. 14.3 - Prob. 27ESCh. 14.3 - Evaluate the iterated integral by converting to...Ch. 14.3 - Evaluate the iterated integral by converting to...Ch. 14.3 - Evaluate the iterated integral by converting to...Ch. 14.3 - Evaluate the iterated integral by converting to...Ch. 14.3 - Evaluate the iterated integral by converting to...Ch. 14.3 - Evaluate the iterated integral by converting to...Ch. 14.3 - Evaluate the iterated integral by converting to...Ch. 14.3 - Determine whether the statement is true or false....Ch. 14.3 - Determine whether the statement is true or false....Ch. 14.3 - If R is the region in the first quadrant between...Ch. 14.3 - The area enclosed by the circle is given by Ch. 14.3 - Evaluate Rx2dA over the region R shown in the...Ch. 14.3 - Show that the shaded area in the accompanying...Ch. 14.3 - (a) Use a double integral in polar coordinated to...Ch. 14.3 - Use polar coordinates to find the volume of the...Ch. 14.3 - Find the area of the region enclosed by the...Ch. 14.3 - Find the area in the first quadrant that is inside...Ch. 14.3 - Discuss how computing a volume of revolution using...Ch. 14.4 - The surface area of a surface of the form z=fx,y...Ch. 14.4 - Consider the surface represented parametrically by...Ch. 14.4 - If ru,v=1ui+1ucosvj+1usinvk then ru=andrv=Ch. 14.4 - If ru,v=1ui+1ucosvj+1usinvk the principal unit...Ch. 14.4 - Suppose is a parametric surface with vector...Ch. 14.4 - Express the area of the given surface as an...Ch. 14.4 - Express the area of the given surface as an...Ch. 14.4 - Express the area of the given surface as an...Ch. 14.4 - Express the area of the given surface as an...Ch. 14.4 - Express the area of the given surface as an...Ch. 14.4 - Express the area of the given surface as an...Ch. 14.4 - Express the area of the given surface as an...Ch. 14.4 - Express the area of the given surface as an...Ch. 14.4 - Express the area of the given surface as an...Ch. 14.4 - Express the area of the given surface as an...Ch. 14.4 - Sketch the parametric surface....Ch. 14.4 - Sketch the parametric surface....Ch. 14.4 - Find a parametric representation of the surface in...Ch. 14.4 - Find a parametric representation of the surface in...Ch. 14.4 - (a) Find parametric equations for the portion of...Ch. 14.4 - (a) Find parametric equations for the portion of...Ch. 14.4 - Find parametric equations for the surface...Ch. 14.4 - Find parametric equations for the surface...Ch. 14.4 - Find a parametric representation of the surface in...Ch. 14.4 - Find a parametric representation of the surface in...Ch. 14.4 - Find a parametric representation of the surface in...Ch. 14.4 - Find a parametric representation of the surface in...Ch. 14.4 - Find a parametric representation of the surface in...Ch. 14.4 - Prob. 24ESCh. 14.4 - Find a parametric representation of the cone...Ch. 14.4 - Describe the cylinder x2+y2=9 in the terms of...Ch. 14.4 - Eliminate the parameters to obtain an equation in...Ch. 14.4 - Eliminate the parameters to obtain an equation in...Ch. 14.4 - Eliminate the parameters to obtain an equation in...Ch. 14.4 - Eliminate the parameters to obtain an equation in...Ch. 14.4 - Eliminate the parameters to obtain an equation in...Ch. 14.4 - Eliminate the parameters to obtain an equation in...Ch. 14.4 - The accompanying figure shows the graphs of two...Ch. 14.4 - The accompanying figure shows the graphs of two...Ch. 14.4 - In each part, the figure shows a portion of the...Ch. 14.4 - In each part, the figure shows a portion of the...Ch. 14.4 - In each part, the figure shows a hemisphere that...Ch. 14.4 - In each part, the figure shows a portion of the...Ch. 14.4 - Find an equation of the tangent plane to the...Ch. 14.4 - Find an equation of the tangent plane to the...Ch. 14.4 - Find an equation of the tangent plane to the...Ch. 14.4 - Find an equation of the tangent plane to the...Ch. 14.4 - Find an equation of the tangent plane to the...Ch. 14.4 - Find an equation of the tangent plane to the...Ch. 14.4 - Find the area of the given surface. The portion of...Ch. 14.4 - Find the area of the given surface. The portion of...Ch. 14.4 - Determine whether the statement is true or false....Ch. 14.4 - Determine whether the statement is true or false....Ch. 14.4 - Determine whether the statement is true or false....Ch. 14.4 - Determine whether the statement is true or false....Ch. 14.4 - Use parametric equations to derive the formula for...Ch. 14.4 - Use parametric equations to derive the formula for...Ch. 14.4 - The portion of the surface z=hax2+y2a,h0 between...Ch. 14.4 - The accompanying figure shows the torus that is...Ch. 14.4 - Prob. 55ESCh. 14.4 - Use a CAS to graph the helicoid...Ch. 14.4 - Use a CAS to graph the pseudosphere...Ch. 14.4 - (a) Find parametric equations for the surface of...Ch. 14.4 - The parametric equations in these exercises...Ch. 14.4 - The parametric equations in these exercises...Ch. 14.4 - The parametric equations in these exercises...Ch. 14.5 - The iterated integral 152436fx,y,zdxdzdy...Ch. 14.5 - Let G be the solid in the first octant bounded...Ch. 14.5 - The volume of the solid G in Quick Check Exercise...Ch. 14.5 - Evaluate the iterated integral....Ch. 14.5 - Evaluate the iterated integral....Ch. 14.5 - Evaluate the iterated integral. 021y21zyzdxdzdyCh. 14.5 - Evaluate the iterated integral....Ch. 14.5 - Evaluate the iterated integral. 0309z20xxydydxdzCh. 14.5 - Evaluate the iterated integral. Ch. 14.5 - Evaluate the iterated integral....Ch. 14.5 - Evaluate the iterated integral....Ch. 14.5 - Evaluate the triple integral. GxysinyzdV, where G...Ch. 14.5 - Evaluate the triple integral. GydV, where G is the...Ch. 14.5 - Evaluate the triple integral. GxyzdV, where G is...Ch. 14.5 - Evaluate the triple integral. Gcosz/ydV, where G...Ch. 14.5 - Use the numerical triple integral operation of a...Ch. 14.5 - Use the numerical triple integral operation of a...Ch. 14.5 - Use a triple integral to find the volume of the...Ch. 14.5 - Use a triple integral to find the volume of the...Ch. 14.5 - Use a triple integral to find the volume of the...Ch. 14.5 - Use a triple integral to find the volume of the...Ch. 14.5 - Let G be the solid enclosed by the surfaces in the...Ch. 14.5 - Let G be the solid enclosed by the surfaces in the...Ch. 14.5 - Set up (but do not evaluate) an iterated triple...Ch. 14.5 - Set up (but do not evaluate) an iterated triple...Ch. 14.5 - Set up (but do not evaluate) an iterated triple...Ch. 14.5 - Set up (but do not evaluate) an iterated triple...Ch. 14.5 - In each part, sketch the solid whose volume is...Ch. 14.5 - In each part, sketch the solid whose volume is...Ch. 14.5 - Determine whether the statement is true or false....Ch. 14.5 - Determine whether the statement is true or false....Ch. 14.5 - Determine whether the statement is true or false....Ch. 14.5 - Determine whether the statement is true or false....Ch. 14.5 - Prob. 31ESCh. 14.5 - Use the result of Exercise 31 to evaluate (a)...Ch. 14.5 - The average value or mean value of a continuous...Ch. 14.5 - The average value or mean value of a continuous...Ch. 14.5 - The average value or mean value of a continuous...Ch. 14.5 - The average value or mean value of a continuous...Ch. 14.5 - Let G be the tetrahedron in the first octant...Ch. 14.5 - Use a triple integral to derive the formula for...Ch. 14.5 - Express each integral as an equivalent integral in...Ch. 14.5 - Express each integral as an equivalent integral in...Ch. 14.6 - (a) The cylindrical wedge 1r3,/6/2,0z5hasvolumeV=....Ch. 14.6 - Let G be the solid region inside the sphere of...Ch. 14.6 - Let G be the solid region describes in Quick Check...Ch. 14.6 - Evaluate the iterated integral. 020101r2zrdzdrdCh. 14.6 - Evaluate the iterated integral....Ch. 14.6 - Evaluate the iterated integral. 0/20/2013sincosdddCh. 14.6 - Evaluate the iterated integral....Ch. 14.6 - Sketch the region G and identify the function f so...Ch. 14.6 - Sketch the region G and identify the function f so...Ch. 14.6 - Sketch the region G and identify the function f so...Ch. 14.6 - Sketch the region G and identify the function f so...Ch. 14.6 - Use cylindrical coordinates to find the volume of...Ch. 14.6 - Use cylindrical coordinates to find the volume of...Ch. 14.6 - Use cylindrical coordinates to find the volume of...Ch. 14.6 - Use cylindrical coordinates to find the volume of...Ch. 14.6 - Use spherical coordinates to find the volume of...Ch. 14.6 - Use spherical coordinates to find the volume of...Ch. 14.6 - Use spherical coordinates to find the volume of...Ch. 14.6 - Use spherical coordinates to find the volume of...Ch. 14.6 - Use cylindrical or spherical coordinates to...Ch. 14.6 - Use cylindrical or spherical coordinates to...Ch. 14.6 - Use cylindrical or spherical coordinates to...Ch. 14.6 - Use cylindrical or spherical coordinates to...Ch. 14.6 - Determine whether the statement is true or false....Ch. 14.6 - Determine whether the statement is true or false....Ch. 14.6 - Determine whether the statement is true or false....Ch. 14.6 - Determine whether the statement is true or false....Ch. 14.6 - (a) Use a CAS to evaluate 2214/6/3rtan31+z2ddrdz...Ch. 14.6 - Use a CAS to evaluate 0/20/40cos17coscos19dddCh. 14.6 - Find the volume enclosed by x2+y2+z2=a2 using (a)...Ch. 14.6 - Let G be the solid in the first octant bounded by...Ch. 14.6 - Find the volume of the solid in the solid in the...Ch. 14.6 - In this exercise we will obtain a formula for the...Ch. 14.6 - Suppose that a triple integral is expressed in...Ch. 14.7 - Let T be the transformation from the u-plane to...Ch. 14.7 - State the relationship between R and S in the...Ch. 14.7 - Let T be the transformation in Quick Check...Ch. 14.7 - The Jacobian of the transformation x=u,y=w,z=2w is...Ch. 14.7 - Find the Jacobian x,y/u,. x=u+4,y=3u5Ch. 14.7 - Find the Jacobian x,y/u,. x=u+22,y=2u2Ch. 14.7 - Prob. 3ESCh. 14.7 - Find the Jacobian x,y/u,. x=2uu2+2,y=2u2+2Ch. 14.7 - Solve for x and y in terms of uand, and then find...Ch. 14.7 - Solve for x and y in terms of uand, and then find...Ch. 14.7 - Solve for x and y in terms of uand, and then find...Ch. 14.7 - Solve for x and y in terms of uand, and then find...Ch. 14.7 - Find the Jacobian x,y,z/u,,w. x=3u+,y=u2w,z=+wCh. 14.7 - Find the Jacobian x,y,z/u,,w. x=uu,y=uuw,z=uwCh. 14.7 - Find the Jacobian x,y,z/u,,w. u=xy,=y,w=x+zCh. 14.7 - Find the Jacobian x,y,z/u,,w. u=x+y+z,=x+yz,w=xy+zCh. 14.7 - Determine whether the statement is true or false....Ch. 14.7 - Determine whether the statement is true or false....Ch. 14.7 - Determine whether the statement is true or false....Ch. 14.7 - Determine whether the statement is true or false....Ch. 14.7 - Sketch the image in the xy-plane of the set S...Ch. 14.7 - Sketch the image in the xy-plane of the set S...Ch. 14.7 - Sketch the image in the xy-plane of the set S...Ch. 14.7 - Sketch the image in the xy-plane of the set S...Ch. 14.7 - Use the transformation u=x2y,=2x+y to find...Ch. 14.7 - Use the transformation u=x+y,=xy to find...Ch. 14.7 - Prob. 23ESCh. 14.7 - Use the transformation u=y/x,=xy to find Rxy3dA...Ch. 14.7 - The transformation x=au,y=ba0,b0 can be rewritten...Ch. 14.7 - The transformation x=au,y=ba0,b0 can be rewritten...Ch. 14.7 - The transformation x=au,y=ba0,b0 can be rewritten...Ch. 14.7 - Show that the area of the ellipse x2a2+y2b2=1 is...Ch. 14.7 - If a, b, and c are positive constants, then the...Ch. 14.7 - If a, b, and c are positive constants, then the...Ch. 14.7 - Find a transformation u=fx,y,=gx,y that when...Ch. 14.7 - Find a transformation u=fx,y,=gx,y that when...Ch. 14.7 - Find a transformation u=fx,y,=gx,y that when...Ch. 14.7 - Find a transformation u=fx,y,=gx,y that when...Ch. 14.7 - Evaluate the integral by making an appropriate...Ch. 14.7 - Evaluate the integral by making an appropriate...Ch. 14.7 - Evaluate the integral by making an appropriate...Ch. 14.7 - Evaluate the integral by making an appropriate...Ch. 14.7 - Use an appropriate change of variables to find the...Ch. 14.7 - Use an appropriate change of variables to find the...Ch. 14.7 - Use the transformation u=x,=zy,w=xy to find...Ch. 14.7 - Use the transformation u=xy,=yz,w=xz to find the...Ch. 14.7 - (a) Verify that...Ch. 14.7 - The formula obtained in part (b) of Exercise 43 is...Ch. 14.7 - The formula obtained in part (b) of Exercise 43 is...Ch. 14.7 - The formula obtained in part (b) of Exercise 43 is...Ch. 14.7 - The three-variable analog of the formula derived...Ch. 14.7 - (a) Consider the transformation x=rcos,y=rsin,z=z...Ch. 14.8 - The total mass of a lamina with continuous density...Ch. 14.8 - Consider a lamina with mass M and continuous...Ch. 14.8 - Let R be the region between the graphs of...Ch. 14.8 - Find the mass and center of gravity of the lamina....Ch. 14.8 - Find the mass and center of gravity of the lamina....Ch. 14.8 - Find the mass and center of gravity of the lamina....Ch. 14.8 - Find the mass and center of gravity of the lamina....Ch. 14.8 - For the given density function, make a conjecture...Ch. 14.8 - For the given density function, make a conjecture...Ch. 14.8 - Make a conjecture about the coordinates of the...Ch. 14.8 - Make a conjecture about the coordinates of the...Ch. 14.8 - Determine whether the statement is true or false....Ch. 14.8 - Determine whether the statement is true or false....Ch. 14.8 - Determine whether the statement is true or false....Ch. 14.8 - Determine whether the statement is true or false....Ch. 14.8 - Show that in polar coordinates the formulas for...Ch. 14.8 - Use the result of Exercise 13 to find the centroid...Ch. 14.8 - Use the result of Exercise 13 to find the centroid...Ch. 14.8 - Use the result of Exercise 13 to find the centroid...Ch. 14.8 - Use the result of Exercise 13 to find the centroid...Ch. 14.8 - Let R be the rectangle bounded by the lines...Ch. 14.8 - Find the centroid of the solid. The tetrahedron in...Ch. 14.8 - The solid bounded by the parabolic cylinder z=1y2...Ch. 14.8 - Find the centroid of the solid. The solid bounded...Ch. 14.8 - Find the centroid of the solid. The solid in the...Ch. 14.8 - Find the centroid of the solid. The solid in the...Ch. 14.8 - Find the centroid of the solid. The solid enclosed...Ch. 14.8 - Find the mass and center of gravity of the solid....Ch. 14.8 - Find the mass and center of gravity of the solid....Ch. 14.8 - Find the mass and center of gravity of the solid....Ch. 14.8 - Find the mass and center of gravity of the solid....Ch. 14.8 - Find the center of gravity of the square lamina...Ch. 14.8 - Find the center of gravity of the cube that is...Ch. 14.8 - Use the numerical triple integral capability of a...Ch. 14.8 - The accompanying figure on the next page shows the...Ch. 14.8 - Use cylindrical coordinates. Find the mass of the...Ch. 14.8 - Use cylindrical coordinates. Find the mass of a...Ch. 14.8 - Use spherical coordinates. Find the mass of a...Ch. 14.8 - Use spherical coordinates. Find the mass of the...Ch. 14.8 - Use cylindrical coordinates to find the centroid...Ch. 14.8 - Use cylindrical coordinates to find the centroid...Ch. 14.8 - Use the Wallis sine and cosine formulas:...Ch. 14.8 - Use the Wallis sine and cosine formulas:...Ch. 14.8 - Use spherical coordinates to find the centroid of...Ch. 14.8 - Use spherical coordinates to find the centroid of...Ch. 14.8 - Find the mass of the solid that is enclosed by the...Ch. 14.8 - Find the center of gravity of the solid bounded by...Ch. 14.8 - Find the center of gravity of the solid that is...Ch. 14.8 - Find the center of gravity of the solid hemisphere...Ch. 14.8 - Find the centroid of the solid that is enclosed by...Ch. 14.8 - Suppose that the density at a point in a gaseous...Ch. 14.8 - The tendency of a lamina to resist a change in...Ch. 14.8 - The tendency of a lamina to resist a change in...Ch. 14.8 - The tendency of a solid to resist a change...Ch. 14.8 - The tendency of a solid to resist a change...Ch. 14.8 - The tendency of a solid to resist a change...Ch. 14.8 - The tendency of a solid to resist a change...Ch. 14.8 - These exercises reference the Theorem of Pappus:...Ch. 14.8 - These exercises reference the Theorem of Pappus:...Ch. 14.8 - These exercises reference the Theorem of Pappus:...Ch. 14.8 - These exercises reference the Theorem of Pappus:...Ch. 14.8 - These exercises reference the Theorem of Pappus:...Ch. 14.8 - It can be proved that if a bounded plane region...Ch. 14 - The double integral over a region R in the...Ch. 14 - The triple integral over a solid G in an...Ch. 14 - (a) Express the area of a region R in the xy-plane...Ch. 14 - (a) Write down parametric equations for a sphere...Ch. 14 - Let R be the region in the accompanying figure....Ch. 14 - Let R be the region shown in the accompanying...Ch. 14 - (a) Find constants a, b, c, and d such that the...Ch. 14 - Give a geometric argument to show that...Ch. 14 - Evaluate the iterated integral. 1/2102xcosx2dydxCh. 14 - Evaluate the iterated integral. 02y2yxey3dxdyCh. 14 - Express the iterated integral as an equivalent...Ch. 14 - Express the iterated integral as an equivalent...Ch. 14 - Sketch the region whose area is represented by the...Ch. 14 - Sketch the region whose area is represented by the...Ch. 14 - Evaluate the double integral. Rx2siny2dA;R is the...Ch. 14 - Evaluate the double integral. R4x2y2dA;R is the...Ch. 14 - Convert to rectangular coordinates and evaluate:...Ch. 14 - Convert to polar coordinates and evaluate:...Ch. 14 - Find the area of the region using a double...Ch. 14 - Find the area of the region using a double...Ch. 14 - Prob. 21RECh. 14 - Convert to spherical coordinates and evaluate:...Ch. 14 - Let G be the region bounded above by the sphere =a...Ch. 14 - Let G=x,y,z:x2+y2z4x. Express the volume of G as...Ch. 14 - Find the volume of the solid using a triple...Ch. 14 - Find the volume of the solid using a triple...Ch. 14 - Find the area of the portion of the surface...Ch. 14 - Find the surface area of the portion of the...Ch. 14 - Find the equation of the tangent plane to the...Ch. 14 - Find the equation of the tangent plane to the...Ch. 14 - Suppose that you have a double integral over a...Ch. 14 - Use the transformation u=x3y,v=3x+y to find...Ch. 14 - Let G be the solid in 3-space defined by the...Ch. 14 - Find the average distance from a point inside a...Ch. 14 - Find the centroid of the region. The region...Ch. 14 - Find the centroid of the region. The upper half of...Ch. 14 - Find the centroid of the solid. The solid cone...Ch. 14 - Find the centroid of the solid. The solid bounded...

Additional Math Textbook Solutions

Find more solutions based on key concepts
1. On a real number line the origin is assigned the number _____ .

Precalculus: Concepts Through Functions, A Unit Circle Approach to Trigonometry (4th Edition)

Find the slopes of the following lines. The line going through the points (2,5)and(2,8).

Calculus & Its Applications (14th Edition)

Whether the graph of y=−f(x) is obtained by areflection about thex- axis of the graph of y=f(x) .

Precalculus Enhanced with Graphing Utilities

Interpreting directional derivatives A function f and a point P are given. Let correspond to the direction of ...

Calculus: Early Transcendentals (2nd Edition)

In Problems 3437, explain what is wrong with the statement. The function f(x) = cosh x is periodic.

Calculus: Single And Multivariable

Determine the signs of six trigonometric functions.

Precalculus

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
SEE MORE TEXTBOOKS
Double and Triple Integrals; Author: Professor Dave Explains;https://www.youtube.com/watch?v=UubU3U2C8WM;License: Standard YouTube License, CC-BY