
In Exercises 45-48, we revisit the four-block, neighborhood discussed in the previous section. Recall that a mail carrier parks her truck at the intersection shown in the figure and then walks to deliver mail to each of the houses. The streets on the outside of the neighborhood have houses on one side only. The interior streets have houses on both sides of the street. On these streets, the mail carrier must walk down the street twice, covering each side of the street separately. A graph that models the streets of the neighborhood walked by the mail carrier is shown.
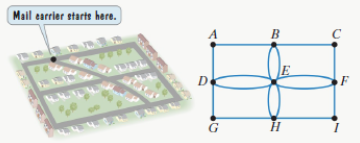
A security guard needs to walk the streets of the neighborhood. Unlike the postal worker, the guard is to walk down each street once, whether or not the street has houses on both sides. Draw a graph that models the streets of the neighborhood walked by the security guard. Then determine whether the residents in the neighborhood will be able to establish a route for the security guard so that each street is walked exactly once. If this is possible, use your map to show where the guard should begin the walk.
Want to see the full answer?
Check out a sample textbook solution
Chapter 14 Solutions
MyLab Math with Pearson eText -- Access Card -- for Thinking Mathematically
- Please Help me answer this linear algebra question. This is a practice textbook question.arrow_forward1. a scientist observed a bacterium in a microscope. it measured about .0000029 meter in diameter which of the following is closest to it? A- 2 x 10^-6, B- 2 x 10^-5, C- 3 x 10^-5, or D- 3 x 10^-6 2.express the product of 500 and 400 in scientific notation. is it 2 x 10^5 or 2 x 10^4 or 2 x 10^3 or 20 x 10^4arrow_forwardExample 4 (Part 1) One of the datasets in the Lock book contains information about 215 countries of the world. One of the variables is the percentage of people in the country who have access to the internet. We have data for 203 of those countries. The plot on the right shows a dotplot of the data. 1. What are the cases? Population n = 203, mean = 43.024 median = 43.5, stdev = 29.259 20 2. What does each dot on the dotplot represent? 15 10 5 20 40 43.024 60 80 3. What type of data is do we collect from the cases, quantitative or categorical?arrow_forward
- No chatgpt pls will upvotearrow_forwardi dont know the anserarrow_forwardLet x be a random variable that represents the percentage of successful free throws a professional basketball player makes in a season. Let y be a random variable that represents the percentage of successful field goals a professional basketball player makes in a season. A random sample of n =6 professional basketball players gave the following information. x 63 79 70 80 84 87 y 46 49 45 55 57 58 Find Se. Round your answer to three decimal places.arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell





