Discrete Mathematics with Graph Theory (Classic Version) (3rd Edition) (Pearson Modern Classics for Advanced Mathematics Series)
3rd Edition
ISBN: 9780134689555
Author: Edgar Goodaire, Michael Parmenter
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 14.2, Problem 1TFQ
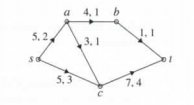
The chain scabt in this network is flow-augmenting.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Problem #1
In the 2010 census, it was reported that the United States had a population of 310 million
people. Of those, 74 million were under the age of 18. If you chose a person from the U.S.
population at random, what is the probability they are under the age of 18?
Problem #2
Given a set S={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, if you were choosing a number at random what is
the probability that you would choose an even number or a number larger than 7?
Answer number two
Answer number one
Chapter 14 Solutions
Discrete Mathematics with Graph Theory (Classic Version) (3rd Edition) (Pearson Modern Classics for Advanced Mathematics Series)
Ch. 14.1 - 1. This directed network illustrates a valid -...Ch. 14.1 - Prob. 2TFQCh. 14.1 - Prob. 3TFQCh. 14.1 - Prob. 4TFQCh. 14.1 - Prob. 5TFQCh. 14.1 - Prob. 6TFQCh. 14.1 - Prob. 7TFQCh. 14.1 - Prob. 8TFQCh. 14.1 - Prob. 9TFQCh. 14.1 - Prob. 10TFQ
Ch. 14.1 - Prob. 1ECh. 14.1 - Prob. 2ECh. 14.1 - Prob. 3ECh. 14.1 - Prob. 4ECh. 14.1 - Answer the following questions for each of the...Ch. 14.1 - Prob. 6ECh. 14.1 - Prob. 7ECh. 14.2 - The chain scabt in this network is...Ch. 14.2 - Prob. 2TFQCh. 14.2 - Prob. 3TFQCh. 14.2 - Prob. 4TFQCh. 14.2 - Prob. 5TFQCh. 14.2 - Prob. 6TFQCh. 14.2 - Prob. 7TFQCh. 14.2 - Prob. 8TFQCh. 14.2 - Prob. 9TFQCh. 14.2 - Prob. 10TFQCh. 14.2 - Answer the following two questions for each of the...Ch. 14.2 - 2. Find a maximum flow for each of the networks in...Ch. 14.2 - Prob. 3ECh. 14.2 - Shown are two networks whose arc capacities are...Ch. 14.3 - 1. To solve a maximum flow problem where are...Ch. 14.3 - Prob. 2TFQCh. 14.3 - Prob. 3TFQCh. 14.3 - Prob. 4TFQCh. 14.3 - Prob. 5TFQCh. 14.3 - Prob. 6TFQCh. 14.3 - Prob. 7TFQCh. 14.3 - Prob. 8TFQCh. 14.3 - If T is a tree, there is a unique path between any...Ch. 14.3 - Prob. 10TFQCh. 14.3 - Prob. 1ECh. 14.3 - Prob. 2ECh. 14.3 - 3. Four warehouses, A,B,C and D. with monthly...Ch. 14.3 - 4. Answer Question 3 again, this time assuming...Ch. 14.3 - Prob. 5ECh. 14.3 - Verify Mengers Theorem, Theorem 14.3.1 for the...Ch. 14.3 - Prob. 7ECh. 14.3 - Prob. 8ECh. 14.3 - Prob. 9ECh. 14.3 - Prob. 10ECh. 14.4 - 1. A graph with 35 vertices cannot have a perfect...Ch. 14.4 - 2. The graph has a perfect matching.
Ch. 14.4 - Prob. 3TFQCh. 14.4 - Prob. 4TFQCh. 14.4 - Prob. 5TFQCh. 14.4 - Prob. 6TFQCh. 14.4 - Prob. 7TFQCh. 14.4 - Prob. 8TFQCh. 14.4 - Prob. 9TFQCh. 14.4 - 10. Hall’s marriage Theorem is named after the...Ch. 14.4 - Prob. 1ECh. 14.4 - :Repeat Exercise 1 with reference to the following...Ch. 14.4 - 3. Determine whether the graph has perfect...Ch. 14.4 - 4. Angela, Brenda, Christine, Helen, Margaret,...Ch. 14.4 - Prob. 5ECh. 14.4 - Bruce, Edgar, Eric, Herb, Maurice, Michael,...Ch. 14.4 - Prob. 7ECh. 14.4 - Prob. 8ECh. 14.4 - Suppose v1,v2 are the bipartition sets in a...Ch. 14.4 - Prob. 10ECh. 14.4 - Prob. 11ECh. 14.4 - Prob. 12ECh. 14.4 - Prob. 13ECh. 14.4 - Prob. 14ECh. 14.4 - Prob. 15ECh. 14.4 - Prob. 16ECh. 14 - Prob. 1RECh. 14 - Prob. 2RECh. 14 - Prob. 3RECh. 14 - Prob. 4RECh. 14 - Prob. 5RECh. 14 - 6.For each network, find a maximum flow and...Ch. 14 - 7.(a) Which graph have the property that for any...Ch. 14 - Prob. 8RECh. 14 - Prob. 9RECh. 14 - Prob. 10RECh. 14 - Prob. 11RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- For the curve defined by r(t) = (e** cos(t), et sin(t)) find the unit tangent vector, unit normal vector, normal acceleration, and tangential acceleration at t = πT 3 T (1) N Ň (1) 133 | aN = 53 ar = = =arrow_forwardFind the tangential and normal components of the acceleration vector for the curve - F(t) = (2t, −3t³, −3+¹) at the point t = 1 - ā(1) = T + Ñ Give your answers to two decimal placesarrow_forwardFind the unit tangent vector to the curve defined by (t)=(-2t,-4t, √√49 - t²) at t = −6. T(−6) =arrow_forward
- answer number 4arrow_forward3. Bayesian Inference – Updating Beliefs A medical test for a rare disease has the following characteristics: Sensitivity (true positive rate): 99% Specificity (true negative rate): 98% The disease occurs in 0.5% of the population. A patient receives a positive test result. Questions: a) Define the relevant events and use Bayes’ Theorem to compute the probability that the patient actually has the disease.b) Explain why the result might seem counterintuitive, despite the high sensitivity and specificity.c) Discuss how prior probabilities influence posterior beliefs in Bayesian inference.d) Suppose a second, independent test with the same accuracy is conducted and is also positive. Update the probability that the patient has the disease.arrow_forwardanswer number 6arrow_forward
- answer number 2arrow_forward4. Linear Regression - Model Assumptions and Interpretation A real estate analyst is studying how house prices (Y) are related to house size in square feet (X). A simple linear regression model is proposed: The analyst fits the model and obtains: • Ŷ50,000+150X YBoB₁X + € • R² = 0.76 • Residuals show a fan-shaped pattern when plotted against fitted values. Questions: a) Interpret the slope coefficient in context. b) Explain what the R² value tells us about the model's performance. c) Based on the residual pattern, what regression assumption is likely violated? What might be the consequence? d) Suggest at least two remedies to improve the model, based on the residual analysis.arrow_forward5. Probability Distributions – Continuous Random Variables A factory machine produces metal rods whose lengths (in cm) follow a continuous uniform distribution on the interval [98, 102]. Questions: a) Define the probability density function (PDF) of the rod length.b) Calculate the probability that a randomly selected rod is shorter than 99 cm.c) Determine the expected value and variance of rod lengths.d) If a sample of 25 rods is selected, what is the probability that their average length is between 99.5 cm and 100.5 cm? Justify your answer using the appropriate distribution.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Minimum cuts and maximum flow rate; Author: Juddy Productions;https://www.youtube.com/watch?v=ylxhl1ipWss;License: Standard YouTube License, CC-BY