Mechanics of Materials
9th Edition
ISBN: 9780133254426
Author: Russell C. Hibbeler
Publisher: Prentice Hall
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 14.2, Problem 14.1P
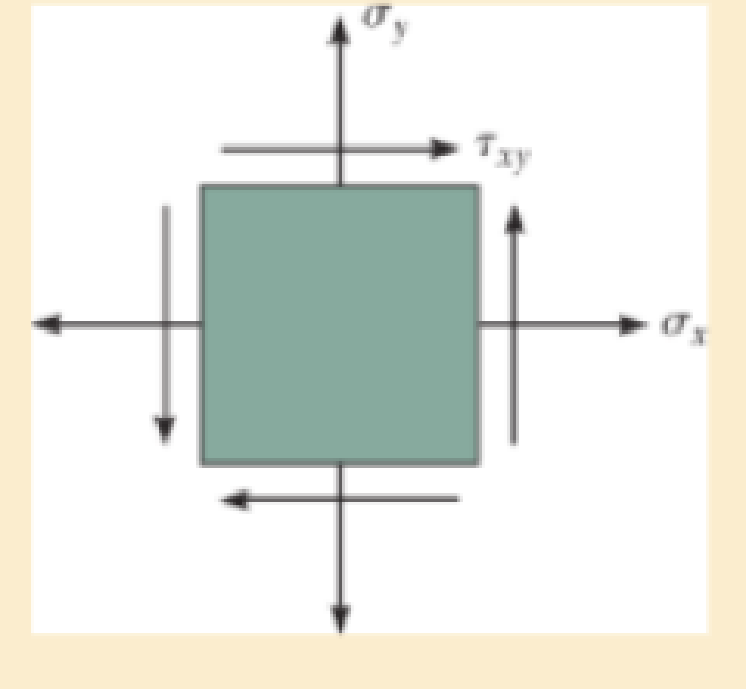
A material is subjected to a general state of plane stress. Express the strain energy density in terms of the elastic constants E, G, and ν and the stress components σx, σy, and τxy.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The normal strain in a suspended bar of material of varying cross section due to its own weight is given by the expression γy/3E where γ = 2.9 lb/in.3 is the specific weight of the material, y = 3.4 in. is the distance from the free (i.e., bottom) end of the bar, L = 17 in. is the length of the bar, and E = 24000 ksi is a material constant. Determine,
(a) the change in length of the bar due to its own weight.
(b) the average normal strain over the length L of the bar.
(c) the maximum normal strain in the bar.
For the state of a plane strain with εx, εy and γxy components: (a) construct Mohr’s circle and (b) determine the equivalent in-plane strains for an element oriented at an angle of 30° clockwise. εx = 255 × 10-6 εy = -320 × 10-6 γxy = -165 × 10-6
Determine the normal strains at the point associated with the x and y axes.
Determine the shear strain at the point associated with the x and y axes.
Determine the normal stresses at the point associated with the x and y axes.
Determine the shear stress at the point.
Determine the normal stress that acts along an axis rotated at θ= 45° counterclockwise from the positive x-axis.
Chapter 14 Solutions
Mechanics of Materials
Ch. 14.2 - A material is subjected to a general state of...Ch. 14.2 - The strain-energy density for plane stress must be...Ch. 14.2 - 14–3. Determine the strain energy in the stepped...Ch. 14.2 - Prob. 14.4PCh. 14.2 - Using bolts of the same material and...Ch. 14.2 - If P = 60 kN, determine the total strain energy...Ch. 14.2 - Determine the maximum force P and the...Ch. 14.2 - *14–8. Determine the torsional strain energy in...Ch. 14.2 - Determine the torsional strain energy in the A-36...Ch. 14.2 - The shaft assembly is fixed at C. The hollow...
Ch. 14.2 - Prob. 14.11PCh. 14.2 - If P = 10 kip, determine the total strain energy...Ch. 14.2 - Determine the maximum force P and the...Ch. 14.2 - Prob. 14.14PCh. 14.2 - 14–15. Determine the bending strain energy stored...Ch. 14.2 - Prob. 14.16PCh. 14.2 - Prob. 14.17PCh. 14.2 - 14–18. Determine the bending strain energy stored...Ch. 14.2 - Prob. 14.19PCh. 14.2 - Prob. 14.20PCh. 14.2 - Prob. 14.21PCh. 14.2 - 14–22. Determine the bending strain energy in the...Ch. 14.2 - Determine the bending strain energy in the...Ch. 14.2 - Determine the bending strain energy in the simply...Ch. 14.3 - 14–25. Determine the horizontal displacement of...Ch. 14.3 - Prob. 14.26PCh. 14.3 - 14–27. Determine the horizontal displacement of...Ch. 14.3 - *14–28. Determine the vertical displacement of...Ch. 14.3 - 14–29. Determine the displacement of point B on...Ch. 14.3 - Determine the vertical displacement of end B of...Ch. 14.3 - Determine the vertical displacement of point S on...Ch. 14.3 - EI is constant. Prob. 1432Ch. 14.3 - The A992 steel bars are pin connected at C and D....Ch. 14.3 - The A992 steel bars are pin connected at C. If...Ch. 14.3 - Determine the slope of the beam at the pin support...Ch. 14.3 - Prob. 14.36PCh. 14.3 - Prob. 14.37PCh. 14.3 - Prob. 14.38PCh. 14.3 - Prob. 14.39PCh. 14.3 - Prob. 14.40PCh. 14.3 - Determine the vertical displacement of end B of...Ch. 14.4 - A bar is 4 m long and has a diameter of 30 mm....Ch. 14.4 - Determine the diameter of a red brass C83400 bar...Ch. 14.4 - Prob. 14.44PCh. 14.4 - The collar has a weight of 50 lb and falls down...Ch. 14.4 - The collar has a weight of 50 lb and falls down...Ch. 14.4 - Prob. 14.47PCh. 14.4 - Prob. 14.48PCh. 14.4 - Prob. 14.49PCh. 14.4 - Prob. 14.50PCh. 14.4 - 14-51. Rods AB and AC have a diameter of 20 mm and...Ch. 14.4 - Prob. 14.52PCh. 14.4 - The composite aluminum 2014T6 bar is made from two...Ch. 14.4 - The composite aluminum 2014-T6 bar is made from...Ch. 14.4 - When the 100-lb block is at h = 3 ft above the...Ch. 14.4 - Prob. 14.56PCh. 14.4 - Prob. 14.57PCh. 14.4 - The tugboat has a weight of 120 000 lb and is...Ch. 14.4 - Prob. 14.59PCh. 14.4 - The weight of 175 lb is dropped from a height of 4...Ch. 14.4 - The weight of 175 lb, is dropped from a height of...Ch. 14.4 - Prob. 14.62PCh. 14.4 - Prob. 14.63PCh. 14.4 - Prob. 14.64PCh. 14.4 - * 14-65. Determine the maximum height h from which...Ch. 14.4 - Prob. 14.66PCh. 14.4 - The overhang beam is made of 2014T6 aluminum....Ch. 14.4 - If the beam is a W1015, determine the maximum...Ch. 14.4 - If the maximum allowable bending stress for the...Ch. 14.4 - A 40-lb weight is dropped from a height of h = 2...Ch. 14.4 - The car bumper is made of...Ch. 14.6 - Determine the vertical displacement of joint A....Ch. 14.6 - Determine the horizontal displacement of joint B....Ch. 14.6 - Determine the vertical displacement of joint B....Ch. 14.6 - Determine the vertical displacement of joint B....Ch. 14.6 - Determine the vertical displacement of joint E....Ch. 14.6 - Prob. 14.77PCh. 14.6 - Prob. 14.78PCh. 14.6 - Determine the horizontal displacement of joint B...Ch. 14.6 - Determine the vertical displacement of joint C of...Ch. 14.6 - 14-81. Determine the horizontal displacement of...Ch. 14.6 - 14-82. Determine the horizontal displacement of...Ch. 14.6 - Determine the vertical displacement of joint A....Ch. 14.6 - The truss is made from A992 steel rods having a...Ch. 14.6 - 14-85. Determine the vertical displacement of...Ch. 14.6 - 14-86. Determine the vertical displacement of...Ch. 14.7 - Determine the displacement at point C. El is...Ch. 14.7 - The beam is made of southern pine for which Ep =...Ch. 14.7 - Determine the displacement at point C. El is...Ch. 14.7 - Determine the slope at point C. El is constant....Ch. 14.7 - Determine the slope at point A. El is constant....Ch. 14.7 - Determine the displacement of point C of the beam...Ch. 14.7 - Determine the slope at B of the beam made from...Ch. 14.7 - The beam is made of Douglas fir. Determine the...Ch. 14.7 - Determine the displacement at pulley B. The A992...Ch. 14.7 - The A992 steel beam has a moment of inertia of I =...Ch. 14.7 - The A992 steel beam has a moment of inertia of I =...Ch. 14.7 - The A992 structural steel beam has a moment of...Ch. 14.7 - Determine the displacement at point C of the...Ch. 14.7 - Determine the slope at A of the shaft. El is...Ch. 14.7 - Determine the slope of end C of the overhang beam....Ch. 14.7 - Determine the displacement of point D of the...Ch. 14.7 - Determine the slope at A of the 2014T6 aluminum...Ch. 14.7 - Prob. 14.104PCh. 14.7 - Prob. 14.105PCh. 14.7 - Determine the displacement at point C of the W14 ...Ch. 14.7 - Determine the slope at A of the W14 26 beam made...Ch. 14.7 - Determine the slope at A. El is constant. Prob....Ch. 14.7 - Determine the slope at C of the overhang white...Ch. 14.7 - Determine the displacement at point D of the...Ch. 14.7 - Determine the maximum deflection of the beam...Ch. 14.7 - Prob. 14.112PCh. 14.7 - Determine the slope of the shaft at the bearing...Ch. 14.7 - Prob. 14.114PCh. 14.7 - Beam AB has a square cross section of 100 mm by...Ch. 14.7 - Beam AB has a square cross section of 100 mm by...Ch. 14.7 - Bar ABC has a rectangular cross section of 300 mm...Ch. 14.7 - Bar ABC has a rectangular cross section of 300 mm...Ch. 14.7 - The L-shaped frame is made from two segments, each...Ch. 14.7 - The L-shaped frame is made from two segments, each...Ch. 14.7 - Prob. 14.121PCh. 14.7 - Prob. 14.122PCh. 14.9 - Solve Prob. 1473 using Castiglianos theorem. 1473....Ch. 14.9 - Solve Prob. 1474 using Castiglianos theorem. 1474....Ch. 14.9 - Prob. 14.125PCh. 14.9 - Prob. 14.126PCh. 14.9 - Prob. 14.127PCh. 14.9 - Prob. 14.128PCh. 14.9 - Prob. 14.129PCh. 14.9 - Prob. 14.130PCh. 14.9 - Prob. 14.131PCh. 14.9 - *14-132. Solve Prob. 14-86 using Castigliano’s...Ch. 14.10 - Solve Prob. 1490 using Castiglianos theorem. 1490....Ch. 14.10 - Solve Prob. 1491 using Castiglianos theorem. 1491....Ch. 14.10 - Prob. 14.135PCh. 14.10 - Solve Prob. 1493 using Castiglianos theorem. 1493....Ch. 14.10 - Solve Prob. 1495 using Castiglianos theorem. 1495....Ch. 14.10 - Solve Prob. 1496 using Castiglianos theorem. 1496....Ch. 14.10 - Prob. 14.139PCh. 14.10 - Prob. 14.140PCh. 14.10 - Prob. 14.141PCh. 14.10 - Solve Prob. 14119 using Castiglianos theorem....Ch. 14.10 - Prob. 14.143PCh. 14.10 - Prob. 14.144PCh. 14.10 - Prob. 14.145PCh. 14 - A = 2300 mm2, I = 9.5(106) mm4. R141Ch. 14 - If the spring at B has a stiffness k = 200 kN/m....Ch. 14 - The spring at B has a stiffness k = 200 kN/m....Ch. 14 - If they each have a diameter of 30 mm, determine...Ch. 14 - and a length of 10 in. It is struck by a hammer...Ch. 14 - Determine the total axial and bending strain...Ch. 14 - The truss is made from A992 steel rods each having...Ch. 14 - The truss is made from A992 steel rods each having...Ch. 14 - El is constant. Use the method of virtual work....Ch. 14 - using Castiglianos theorem. R149. The cantilevered...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
List several uses of the arbor press.
Machine Tool Practices (10th Edition)
The triple jump is a track-and-field event in which an athlete gets a running start and tries to leap as far as...
Vector Mechanics For Engineers
Steady state conduction rate to the warm compressor to the net power produces theoretically by thermodynamic ba...
Introduction to Heat Transfer
What is the importance of modeling in engineering? How are the mathematical models for engineering processes pr...
HEAT+MASS TRANSFER:FUND.+APPL.
3.3 It is known that a vertical force of 200 lb is required to remove the nail at C from the board. As the nail...
Vector Mechanics for Engineers: Statics, 11th Edition
Convert the following quantities from English to SI units: a. 98 Btu/(hr-ft-F) b. 0.24 Btu/(lbm-F) C. 0.04 Ibm/...
Heating Ventilating and Air Conditioning: Analysis and Design
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- The piece of plastic is originally rectangular. Determine the average normal strain that occurs along the diagonals AC and DB. Determine the shear strain at corners A and B if the plastic distorts as shown by the dashed lines.arrow_forwardThe normal strain in a suspended bar of material of varying cross section due to its own weight is given by the expression yy/3E where y = 2.3 lb/in.³ is the specific weight of the material, y = 2.4 in. is the distance from the free (i.e., bottom) end of the bar, L = 6 in. is the length of the bar, and E= 24000 ksi is a material constant. Determine, (a) the change in length of the bar due to its own weight. (b) the average normal strain over the length L of the bar (c) the maximum normal strain in the bar. Answer: (a) d = i (b) avg (c) Emax || MI Mi x10-6 in. με μεarrow_forwardThe normal strain in a suspended bar of material of varying cross section due to its own weight is given by the expression yy/3E where y = 3.0 lb/in.³ is the specific weight of the material, y = 6.3 in. is the distance from the free (i.e., bottom) end of the bar, L = 21 in. is the length of the bar, and E = 27000 ksi is a material constant. Determine, (a) the change in length of the bar due to its own weight. (b) the average normal strain over the length L of the bar (c) the maximum normal strain in the bar. Answer: (a) d = i (b) avg (c) Emax i x10-6 in. με μεarrow_forward
- In many situations it is known that the normal stress in a given direc-tion is zero. For example, σz= 0 in the case of the thin plate shown. For this case, which is known as plane stress, show that if the strains εx and εy have been determined experimentally, we can express σx, σyand εz as follows:arrow_forwardThe normal strain in a suspended bar of material of varying cross section due to its own weight is given by the expression yy/3E where y=2.4 lb/in.³ is the specific weight of the material, y = 0.6 in. is the distance from the free (i.e., bottom) end of the bar, L = 6 in. is the length of the bar, and E=30000 ksi is a material constant. Determine, (a) the change in length of the bar due to its own weight. (b) the average normal strain over the length L of the bar (c) the maximum normal strain in the bar. Answer: (a) 5 = 1 (b) Sa (c) Emax= i x10-6 in. με μεarrow_forwardThe normal strain in a suspended bar of material of varying cross section due to its own weight is given by the expression yy/3E where y = 2.4 lb/in.³ is the specific weight of the material, y = 1.8 in. is the distance from the free (i.e., bottom) end of the bar, L = 9 in. is the length of the bar, and E= 26000 ksi is a material constant. Determine, (a) the change in length of the bar due to its own weight. (b) the average normal strain over the length L of the bar. (c) the maximum normal strain in the bar. Calculate the change in length of the bar due to its own weight. Answer: x10-6 in.arrow_forward
- The normal strain in a suspended bar of material of varying cross section due to its own weight is given by the expression yy/3E where y = 2.9 lb/in.³ is the specific weight of the material, y = 0.5 in. is the distance from the free (i.e., bottom) end of the bar, L = 5 in. is the length of the bar, and E = 25000 ksi is a material constant. Determine, (a) the change in length of the bar due to its own weight. (b) the average normal strain over the length L of the bar. (c) the maximum normal strain in the bar. Part 1 * Your answer is incorrect. Calculate the change in length of the bar due to its own weight. Answer: d= i 2.416 eTextbook and Media x10-6 in.arrow_forwardThe normal strain in a suspended bar of material of varying cross section due to its own weight is given by the expression yy/3E where y = 2.9 lb/in.³ is the specific weight of the material, y = 0.5 in. is the distance from the free (i.e., bottom) end of the bar, L = 5 in. is the length of the bar, and E = 25000 ksi is a material constant. Determine, (a) the change in length of the bar due to its own weight. (b) the average normal strain over the length L of the bar. (c) the maximum normal strain in the bar.arrow_forwardAt a certain section in a material under stress, direct stresses of 45 MN/m2 tensile and 75 MN/m2 tensile act on perpendicular planes together with a shear stress τ acting on these planes. If the maximum stress in the material is limited to 150 MN/m2 tensile, determine the value of τ.arrow_forward
- A thin polymer plate PQR is deformed such that corner Q is displaced downward a distance L = 0.10 in. to new position Q' as shown. Determine the magnitude of the shear strain at Q' associated with the two edges (PQ and QR). P 25 in. 7982 μrad 6862 μrad 09533 μrad O6186 prad O8600 μrad 4 in. R 10 in. L Xarrow_forwardA state of stress at a point A is given by σx = 25 MPa, σy = 122 MPa, and τxy = 60 MPa. Determine the equivalent state of stress on an element at the point which represents the principal stresses.arrow_forwardThe normal strain in a suspended bar of material of varying cross section due to its own weight is given by the expression yy/3E where y = 2.0 lb/in.³ is the specific weight of the material, y = 2.8 in. is the distance from the free (i.e., bottom) end of the bar, L = 14 in. is the length of the bar, and E = 20000 ksi is a material constant. Determine, (a) the change in length of the bar due to its own weight. (b) the average normal strain over the length L of the bar (c) the maximum normal strain in the bar. Answer: (a) 8- i (b) Eavg (c) Emax = i x10-6 in. με μεarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
An Introduction to Stress and Strain; Author: The Efficient Engineer;https://www.youtube.com/watch?v=aQf6Q8t1FQE;License: Standard YouTube License, CC-BY