Math in Our World
3rd Edition
ISBN: 9780073519678
Author: David Sobecki Professor, Allan G. Bluman
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 14.1, Problem 1TTO
Draw a graph to represent ferry service between northern Ohio and some Lake Erie islands shown in Figure 14-4.
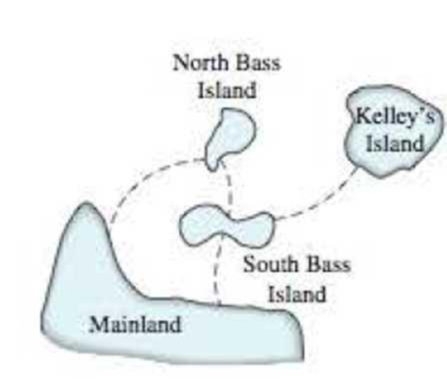
Figure 14-4
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
: +0
العنوان
I need a detailed drawing with explanation
しじ
ined sove in peaper
Anoting
Q4// Draw and Evaluate √√√xy-²sin(y²)dydx
PU+96er
Lake
Ge
Q3// Find the volume of the region between the cylinder 2 = y² and the xy-
plane that is bounded by the planes x = 1, x = 2, y = -2, and y = 2.
T
M
University of Babylon
Faculty of Engineering-AIMusyab
Automobile Eng. Dep.
Year: 2022-2023,
2 Course, 1 Attempt
Note: Answer five questions only.
Stage Third
Subject: Numerical
Analysis
Date: 2023\\
Time: 3 Hour
Q1: Solve the poisson equation [Uxx + Uyy = -81xy),
[
Ministry of Higher Education &
Scientific Research
Babylon University
College of Engineering-
Al musayab
Subject :Numerical Analysis
Stage:Third
Time: 2 hour
Automobile Department
Date:26-3-2023
nd
1st month exam/2"
semester (2022-2023)
Note: Answer all questions, all questions have same degree.
Q1: Use Newton's method to find solutions to the system with two
step Take (X,Yo)=(8,10).
{
x35x2 + 2xy + 13 = 0
x3 + x²-14x-y-19=0
Q2/:Solve the system by Gauss-Seidel iterative method.(Perform only
three iterations).
8x-3y+2z-20
4x+11y-z-33
6x+3y+12z-35
03/:Curve fit the data using a power function
X
2
4
8
5
6
0.7500
0.1875
0.1200
0.0833
0.0469
Chapter 14 Solutions
Math in Our World
Ch. 14.1 - Draw a graph to represent ferry service between...Ch. 14.1 - The floor plan shown in Figure 14-7 is for a...Ch. 14.1 - Prob. 3TTOCh. 14.1 - Draw a graph for my neighborhood, shown in Figure...Ch. 14.1 - Prob. 5TTOCh. 14.1 - Prob. 6TTOCh. 14.1 - Prob. 7TTOCh. 14.1 - Prob. 8TTOCh. 14.1 - Prob. 1ECh. 14.1 - What is the difference between a loop and a...
Ch. 14.1 - What is the difference between a circuit and a...Ch. 14.1 - Draw two graphs that look physically different but...Ch. 14.1 - Prob. 5ECh. 14.1 - Prob. 8ECh. 14.1 - Prob. 9ECh. 14.1 - Prob. 10ECh. 14.1 - Prob. 11ECh. 14.1 - How does graph coloring apply to maps?Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Prob. 18ECh. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Prob. 20ECh. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Use the following graph to answer Exercises 1324....Ch. 14.1 - Prob. 25ECh. 14.1 - Prob. 26ECh. 14.1 - Prob. 27ECh. 14.1 - Prob. 28ECh. 14.1 - Prob. 29ECh. 14.1 - Prob. 30ECh. 14.1 - For Exercises 3134, represent each figure using a...Ch. 14.1 - Prob. 32ECh. 14.1 - Prob. 33ECh. 14.1 - Prob. 34ECh. 14.1 - Prob. 35ECh. 14.1 - Prob. 36ECh. 14.1 - For Exercises 3538, draw a graph to represent each...Ch. 14.1 - Prob. 38ECh. 14.1 - Prob. 39ECh. 14.1 - For Exercises 3942, draw a graph that represents...Ch. 14.1 - Prob. 41ECh. 14.1 - Prob. 42ECh. 14.1 - In Exercises 4350, use graph coloring to find the...Ch. 14.1 - Prob. 44ECh. 14.1 - Prob. 45ECh. 14.1 - Prob. 46ECh. 14.1 - In Exercises 4350, use graph coloring to find the...Ch. 14.1 - Prob. 48ECh. 14.1 - Prob. 49ECh. 14.1 - Prob. 50ECh. 14.1 - Prob. 51ECh. 14.1 - Prob. 52ECh. 14.1 - Prob. 53ECh. 14.1 - Prob. 54ECh. 14.1 - Prob. 55ECh. 14.1 - Draw a graph that represents the street map in...Ch. 14.1 - Prob. 57ECh. 14.1 - Prob. 58ECh. 14.1 - Prob. 59ECh. 14.1 - Prob. 61ECh. 14.1 - Prob. 62ECh. 14.1 - Prob. 63ECh. 14.1 - (a)When a graph represents a map as in Exercise...Ch. 14.2 - Use Eulers theorem to determine if the graphs...Ch. 14.2 - Prob. 2TTOCh. 14.2 - Prob. 3TTOCh. 14.2 - Prob. 1ECh. 14.2 - Prob. 2ECh. 14.2 - Prob. 3ECh. 14.2 - Prob. 4ECh. 14.2 - Prob. 5ECh. 14.2 - Prob. 6ECh. 14.2 - For Exercises 710, decide whether each connected...Ch. 14.2 - Prob. 8ECh. 14.2 - For Exercises 710, decide whether each connected...Ch. 14.2 - Prob. 10ECh. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - Prob. 12ECh. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - Prob. 14ECh. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - Prob. 16ECh. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - Prob. 18ECh. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - For Exercises 1120, (a)State whether the graph has...Ch. 14.2 - Prob. 21ECh. 14.2 - Prob. 22ECh. 14.2 - Prob. 23ECh. 14.2 - Prob. 24ECh. 14.2 - Prob. 25ECh. 14.2 - For Exercises 2126, draw a graph for the figures...Ch. 14.2 - Prob. 27ECh. 14.2 - Prob. 28ECh. 14.2 - Prob. 29ECh. 14.2 - Prob. 30ECh. 14.2 - Prob. 31ECh. 14.2 - Prob. 32ECh. 14.2 - For Exercises 33 and 34, determine if an Euler...Ch. 14.2 - For Exercises 33 and 34, determine if an Euler...Ch. 14.2 - Prob. 35ECh. 14.2 - Prob. 37ECh. 14.2 - Prob. 38ECh. 14.2 - Draw some sample graphs and use them to discuss...Ch. 14.2 - Prob. 40ECh. 14.2 - Prob. 41ECh. 14.2 - Prob. 42ECh. 14.2 - Explain why the word connected is crucial...Ch. 14.2 - Prob. 44ECh. 14.2 - Prob. 45ECh. 14.2 - Prob. 46ECh. 14.3 - Find a Hamilton path that begins at vertex C for...Ch. 14.3 - Prob. 2TTOCh. 14.3 - Prob. 3TTOCh. 14.3 - The driving times in minutes between four cities...Ch. 14.3 - Prob. 5TTOCh. 14.3 - Prob. 6TTOCh. 14.3 - Prob. 7TTOCh. 14.3 - What is the difference between a Hamilton path and...Ch. 14.3 - Prob. 2ECh. 14.3 - Give an example of a problem in our world that can...Ch. 14.3 - Prob. 4ECh. 14.3 - Prob. 5ECh. 14.3 - Prob. 6ECh. 14.3 - Describe what a typical traveling salesperson...Ch. 14.3 - Prob. 8ECh. 14.3 - Prob. 9ECh. 14.3 - Prob. 10ECh. 14.3 - For Exercises 1118, find two different Hamilton...Ch. 14.3 - Prob. 12ECh. 14.3 - Prob. 13ECh. 14.3 - Prob. 14ECh. 14.3 - For Exercises 1118, find two different Hamilton...Ch. 14.3 - Prob. 16ECh. 14.3 - Prob. 17ECh. 14.3 - Prob. 18ECh. 14.3 - For Exercises 1118, find two different Hamilton...Ch. 14.3 - Prob. 20ECh. 14.3 - Prob. 21ECh. 14.3 - Prob. 22ECh. 14.3 - For Exercises 1924, find two different Hamilton...Ch. 14.3 - Prob. 24ECh. 14.3 - Prob. 25ECh. 14.3 - Prob. 26ECh. 14.3 - For Exercises 2528, find the number of Hamilton...Ch. 14.3 - Prob. 28ECh. 14.3 - Prob. 29ECh. 14.3 - For Exercises 29 and 30, use the brute force...Ch. 14.3 - For Exercises 3134, use the nearest neighbor...Ch. 14.3 - Prob. 32ECh. 14.3 - Prob. 33ECh. 14.3 - Prob. 34ECh. 14.3 - In Exercises 3538, use the cheapest link algorithm...Ch. 14.3 - Prob. 36ECh. 14.3 - Prob. 37ECh. 14.3 - Prob. 38ECh. 14.3 - Prob. 39ECh. 14.3 - For Exercises 3942, use the information in the...Ch. 14.3 - Prob. 41ECh. 14.3 - Prob. 42ECh. 14.3 - Prob. 43ECh. 14.3 - For Exercises 4346, use the information in the...Ch. 14.3 - For Exercises 4346, use the information in the...Ch. 14.3 - Prob. 46ECh. 14.3 - Prob. 47ECh. 14.3 - A pizza delivery person has five prearranged...Ch. 14.3 - Prob. 49ECh. 14.3 - Prob. 50ECh. 14.3 - Prob. 51ECh. 14.3 - Prob. 52ECh. 14.3 - When planning routes, distance isnt always the key...Ch. 14.3 - Prob. 54ECh. 14.3 - Repeat questions 51 through 54, choosing four...Ch. 14.3 - Prob. 56ECh. 14.3 - Prob. 57ECh. 14.3 - Prob. 58ECh. 14.3 - Find a road atlas that has a mileage chart. Pick...Ch. 14.3 - Prob. 60ECh. 14.3 - Prob. 61ECh. 14.3 - Prob. 62ECh. 14.3 - Prob. 63ECh. 14.3 - Prob. 64ECh. 14.3 - Prob. 65ECh. 14.3 - Prob. 66ECh. 14.4 - Prob. 1TTOCh. 14.4 - Prob. 2TTOCh. 14.4 - Prob. 3TTOCh. 14.4 - Prob. 4TTOCh. 14.4 - Prob. 5TTOCh. 14.4 - Prob. 1ECh. 14.4 - Prob. 2ECh. 14.4 - Prob. 3ECh. 14.4 - Prob. 4ECh. 14.4 - Prob. 5ECh. 14.4 - Prob. 6ECh. 14.4 - For Exercise 716, decide whether or not each graph...Ch. 14.4 - Prob. 8ECh. 14.4 - Prob. 9ECh. 14.4 - Prob. 10ECh. 14.4 - Prob. 11ECh. 14.4 - Prob. 12ECh. 14.4 - Prob. 13ECh. 14.4 - Prob. 14ECh. 14.4 - Prob. 15ECh. 14.4 - Prob. 16ECh. 14.4 - Prob. 17ECh. 14.4 - Prob. 18ECh. 14.4 - Prob. 19ECh. 14.4 - Prob. 20ECh. 14.4 - Prob. 21ECh. 14.4 - Prob. 22ECh. 14.4 - Prob. 23ECh. 14.4 - Prob. 24ECh. 14.4 - Prob. 25ECh. 14.4 - Prob. 26ECh. 14.4 - Prob. 27ECh. 14.4 - Prob. 28ECh. 14.4 - Prob. 29ECh. 14.4 - Prob. 30ECh. 14.4 - Prob. 31ECh. 14.4 - Prob. 32ECh. 14.4 - Prob. 33ECh. 14.4 - As a new suburban neighborhood is being built, the...Ch. 14.4 - Prob. 35ECh. 14.4 - Prob. 36ECh. 14.4 - Prob. 37ECh. 14.4 - Prob. 38ECh. 14.4 - Prob. 39ECh. 14.4 - In the last two sections, we used both Hamilton...Ch. 14.4 - Prob. 41ECh. 14.4 - Prob. 42ECh. 14 - Use the graph shown in Figure 14-62 for Exercise...Ch. 14 - Prob. 2RECh. 14 - Prob. 3RECh. 14 - Prob. 4RECh. 14 - Prob. 5RECh. 14 - Prob. 6RECh. 14 - Use the graph shown in Figure 14-62 for Exercises...Ch. 14 - Prob. 8RECh. 14 - Prob. 9RECh. 14 - Prob. 10RECh. 14 - Prob. 11RECh. 14 - Prob. 12RECh. 14 - Prob. 13RECh. 14 - Repeat Exercise 13 for the graphs from Exercises...Ch. 14 - Prob. 15RECh. 14 - Prob. 16RECh. 14 - Prob. 17RECh. 14 - Prob. 18RECh. 14 - Prob. 19RECh. 14 - Prob. 20RECh. 14 - Prob. 21RECh. 14 - Prob. 22RECh. 14 - Prob. 23RECh. 14 - Prob. 24RECh. 14 - Prob. 25RECh. 14 - Prob. 26RECh. 14 - Prob. 27RECh. 14 - Prob. 28RECh. 14 - Prob. 29RECh. 14 - Prob. 30RECh. 14 - Prob. 31RECh. 14 - Prob. 32RECh. 14 - Prob. 33RECh. 14 - Prob. 34RECh. 14 - For the following graph: (a)What is the degree of...Ch. 14 - Draw a graph with two bridges, and the...Ch. 14 - Prob. 3CTCh. 14 - Prob. 4CTCh. 14 - (a)For the graph shown in Figure 14-73, find an...Ch. 14 - Prob. 6CTCh. 14 - For the housing plan shown in Figure 14-75, draw a...Ch. 14 - Prob. 8CTCh. 14 - Use the brute force method to find the shortest...Ch. 14 - Use the nearest neighbor method and cheapest link...Ch. 14 - Prob. 11CTCh. 14 - Decide whether the problem can be solved using...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- University of Babylon Faculty of Engineering-AlMusyab Automobile Eng. Dep. Year: 2022-2023, 2nd Course, 1 Attempt Stage: Third Subject: Numerical Analysis Date: 2023\\ Time: 3 Hour dy = x + yl Q5-A: Using Euler's method, find an approximate value of (y) corresponding to (x=0.3),given that[- and [y=1 when x=0].(taking h=0.1). dx (10 M) Q5-B Find a root of an equation[f(x)=x-x-1] using Newton Raphson method to an accuracy of &=0. (10 M) Q6:Using Newton's divided differences formula, evaluate f(8) given: X 4 58 7 103 11 13 Y=f(x) 48 100 900 294 1210 2028 (20 M) Lexaminer: Examiner: Good luck W Head of Department:arrow_forwardQ5: Discuss the stability critical point of the ODEs x + (*)² + 2x² = 2 and draw the phase portrait. (10M)arrow_forwardA retail store manager claims that the average daily sales of the store are $1,500. You aim to test whether the actual average daily sales differ significantly from this claimed value. You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. Showing the calculation is a must. If calculation is missing,so please provide a step by step on the answers Numerical answers in the yellow cellsarrow_forward
- . The students who attend Memorial High School have a wide variety of extra-curricular activities to choose from in the after-school program. Students are 38% likely to join the dance team; 18% likely to participate in the school play; 42% likely to join the yearbook club; and 64% likely to join the marching band. Many students choose to participate in multiple activities. Students have equal probabilities of being freshmen, sophomores, juniors, or seniors.What is the probability of the union of being either a freshman or senior? 0.07 0.44 0.50 0.25arrow_forwardExplain the conditions under which the Radius of Convergence of the Power Series is a "finite positive real number" r>0arrow_forwardNo chatgpt pls will upvotearrow_forward
- Q/By using Hart man theorem study the Stability of the critical points and draw the phase portrait of the system:- X = -4x+2xy - 8 y° = 4y² X2arrow_forwardThis means that when the Radius of Convergence of the Power Series is a "finite positive real number" r>0, then every point x of the Power Series on (-r, r) will absolutely converge (x ∈ (-r, r)). Moreover, every point x on the Power Series (-∞, -r)U(r, +∞) will diverge (|x| >r). Please explain it.arrow_forwardExplain the conditions under which Radious of Convergence of Power Series is infinite. Explain what will happen?arrow_forward
- Explain the conditions under Radius of Convergence which of Power Series is 0arrow_forwardExplain the key points and reasons for 12.8.2 (1) and 12.8.2 (2)arrow_forwardQ1: A slider in a machine moves along a fixed straight rod. Its distance x cm along the rod is given below for various values of the time. Find the velocity and acceleration of the slider when t = 0.3 seconds. t(seconds) x(cm) 0 0.1 0.2 0.3 0.4 0.5 0.6 30.13 31.62 32.87 33.64 33.95 33.81 33.24 Q2: Using the Runge-Kutta method of fourth order, solve for y atr = 1.2, From dy_2xy +et = dx x²+xc* Take h=0.2. given x = 1, y = 0 Q3:Approximate the solution of the following equation using finite difference method. ly -(1-y= y = x), y(1) = 2 and y(3) = −1 On the interval (1≤x≤3).(taking h=0.5).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY