Chapter 14, Problem 47SE

Have you ever wondered whether soccer players suffer adverse effects from hitting “headers”? The authors of the article “No Evidence of Impaired Neurocognitive Performance in Collegiate Soccer Players” (Amer. J. of Sports Med., 2002: 157–162) investigated this issue from several perspectives.

a. The paper reported that 45 of the 91 soccer players in their sample had suffered at least one concussion, 28 of 96 nonsoccer athletes had suffered at least one concussion, and only 8 of 53 student controls had suffered at least one concussion. Analyze this data and draw appropriate conclusions.

b. For the soccer players, the sample correlation coefficient calculated from the values of x = soccer exposure (total number of competitive seasons played prior to enrollment in the study) and y = score on an immediate memory recall test was r = −.220. Interpret this result.

c. Here is summary information on scores on a controlled oral word-association test for the soccer and nonsoccer athletes:

  $\begin{array}{l}n1=26,x_1=37.50,s_1=9.13\hfill \\ n2=56,x_2=39.63,s_2=10.19\hfill \end{array}$

Analyze this data and draw appropriate conclusions.

d. Considering the number of prior nonsoccer concussions, the values of mean 6 sd for the three groups were .30 ± .67, .49 ± .87, and .19 ± .48. Analyze this data and draw appropriate conclusions.

To determine

Analyze the given data and draw conclusions.

Answer to Problem 47SE

There is sufficient evidence to conclude that there is a difference in the proportion of concussion with respect to three groups.

Explanation of Solution

Given info:

The report says that 45 out of 91 soccer players had suffered at least one concussion, 28 of 96 non-soccer athletes suffered at least one concussion and 8 of 53 students had at least one concussion.

Calculation:

From the given data the following can be observed,

Group	Concussion	No concussion	Total
Soccer	45	46	91
Non soccer	28	68	96
student	8	45	53
Total	81	159	240

The claim is to test whether there is any homogeneity among the proportion of concussions with respect to the three groups. If the claim is rejected, then there is no homogeneity among the proportion of concussions with respect to the three groups.

Null hypothesis:

$H_0:p_{1j}=p_{2j}=p_{3j}$

That is, the proportion of concussions is homogenous with respect to the three groups.

Alternative hypothesis:

$H_a:$ The proportion of concussions is not homogenous with respect to the three groups.

Test statistic:

Software procedure:

Step-by-step procedure to find the chi-square test statistic using MINITAB is given below:

• Choose Stat > Tables > Chi-Square Test (Two-Way Table in Worksheet).
• In Columns containing the table, enter the columns of Concussion and Nonconcussion.
• Click OK.

Output obtained from MINITAB is given below:

Decision rule:

If $P\text{-value}>\alpha$, then fail to reject the null hypothesis $\left(H_0\right)$.

If $P\text{-value}<\alpha$, then reject the null hypothesis $\left(H_0\right)$.

Conclusion:

The P-value is 0.000 and the least level of significance is 0.001.

The P-value is lesser than the level of significance.

That is, $0.000\left(=P\text{-value}\right)<0.001\left(=\alpha \right)$

Thus, the null hypothesis isrejected.

Hence, there is sufficient evidence to conclude that there is a difference in the proportion of concussion with respect to three groups.

To determine

Interpret the given results.

Answer to Problem 47SE

There is no sufficient evidence to conclude that there exists a negative correlation or association in the population at 1% level of significance.

Explanation of Solution

Given info:

The sample correlation coefficient for the soccer players group is calculated by using the soccer exposure x and the score on an immediate memory recall test y and it is –0.220.

Calculation:

Testing the significance of correlation:

Null hypothesis:

$H_0:\rho =0$

That is, there is no correlation between x and y.

Alternative hypothesis:

$H_a:\rho <0$

That is, there is a negative correlation between x and y.

Test statistic:

$t=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}$

Where,

r represents the correlation coefficient value.

n represents the total sample size.

Substitute r as –0.220 and n as 91.

$\begin{array}{c}t=\frac{-0.220\sqrt{91-2}}{\sqrt{1-{\left(-0.220\right)}^2}}\\ =\frac{-0.220\sqrt{89}}{\sqrt{1-0.0484}}\\ =\frac{-0.220\left(9.43\right)}{0.975}\\ \approx -2.13\end{array}$

Thus, the test statistic is –2.13.

P-value:

Software procedure:

Step-by-step procedure to obtain the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select t, enter 89 in degrees of freedom..
• Under Shaded Area Tab select X value under Define Shaded Area By and select left tail.
• Choose X value as –2.13.
• Click OK.

Output obtained from MINITAB is given below:

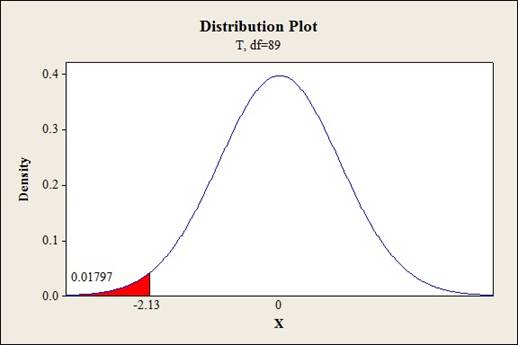
Conclusion:

The P-valueis 0.018 and the level of significance is 0.01.

The P-valueis lesser than the level of significance.

That is, $0.018\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected.

Hence, there is no sufficient evidence to conclude that there exists a negative correlation or association in the population at 1% level of significance.

To determine

Analyze the given data and draw conclusions.

Answer to Problem 47SE

There is sufficient evidence to conclude that the average scores of two groups are the same.

Explanation of Solution

Given info:

An oral test was conducted for soccer and non-soccer athletes. The summary statistics are given below:

$\begin{array}{l}{n}_1=26,{\overline{x}}_1=37.50,s_1=9.13\\ n_2=56,{\overline{x}}_2=39.63,s_2=10.19\end{array}$

Calculation:

Testing the hypothesis:

Null hypothesis:

$H_0:{\mu }_1={\mu }_2$

That is, the average test score is same for the two groups.

Alternative hypothesis:

$H_a:{\mu }_1\ne {\mu }_2$

That is, the average test score is not the same for the two groups.

Test statistic:

Software procedure:

Step-by-step procedure to obtain the test statistic using MINITAB is given below:

• Choose Stat > Basic Statistics > 2-Sample t.
• Choose Summarized data.
• In first, enter Sample size as 26, Mean as 37.50, Standard deviation as 9.13.
• In second, enter Sample size as56, Mean as 39.63, Standard deviation as 10.19.
• Select Assume equal variances.
• Choose Options.
• In Confidence level, enter 95.
• Choose not equal in Alternative.
• Click OK.

Output obtained from MINITAB is given below:

Conclusion:

The P-value is 0.366 and the level of significance is 0.10.

The P-value is greater than the level of significance.

That is, $0.366\left(=P\text{-value}\right)>0.10\left(=\alpha \right)$

Thus, the null hypothesis is not rejected.

Hence, there is sufficient evidence to conclude that the average scores of two groups are the same.

To determine

Analyze the given data and draw conclusions.

Answer to Problem 47SE

There is sufficient evidence to conclude that there is a difference in the average number of prior non-soccer concussion between the three groups.

Explanation of Solution

Given info:

The mean plus or standard deviation for the three groups with respect to the number of prior non-soccer concussions are $0.30\pm 0.67,0.49\pm 0.87,0.19\pm 0.48$.

Calculation:

Testing the hypothesis:

Null hypothesis:

$H_0:$ All means are equal.

That is, there is no difference in the average number of prior non-soccer concussion between the three groups.

Alternative hypothesis:

$H_a:$ At least one of the means is not equal.

That is, there is a difference in the average number of prior non-soccer concussion between the three groups.

Test statistic:

$f=\frac{MS{T}_r}{MSE}$

Where,

$MS{T}_r$ represents the mean sum of squares with respect to the three groups.

MSE represents the mean sum of squares due to error.

Sum of squares with respect to the three groups is calculated as follows:

$\begin{array}{c}SS{T}_r=n_1{\left({\overline{x}}_1-\overline{\overline{x}}\right)}^2+n_2{\left({\overline{x}}_2-\overline{\overline{x}}\right)}^2+n_3{\left({\overline{x}}_3-\overline{\overline{x}}\right)}^2\\ =91{\left(0.30-0.34\right)}^2+96{\left(0.49-0.34\right)}^2+53{\left(0.19-0.34\right)}^2\\ =91\left(0.0016\right)+96\left(0.0225\right)+53\left(0.0225\right)\\ =0.1456+2.16+1.1925\end{array}$

$=3.4981$

Where,

$\begin{array}{c}\overline{\overline{x}}=\frac{{\overline{x}}_1+{\overline{x}}_2+{\overline{x}}_3}{n}\\ =\frac{45+28+8}{91+96+53}\\ =\frac{81}{240}\\ \approx 0.34\end{array}$

Mean sum of squares due to treatment:

$\begin{array}{c}MS{T}_r=\frac{SS{T}_r}{2}\\ =\frac{3.4981}{2}\\ =1.7491\end{array}$

Sum of squares due to error:

$\begin{array}{c}SSE=\left(n_1-1\right){\sigma }_1^2+\left(n_2-1\right){\sigma }_2^2+\left(n_3-1\right){\sigma }_3^2\\ =\left(91-1\right){\left(0.67\right)}^2+\left(96-1\right){\left(0.87\right)}^2+\left(53-1\right){\left(0.48\right)}^2\\ =\left(90\right)\left(0.4489\right)+\left(95\right)\left(0.7569\right)+\left(52\right)\left(0.2304\right)\\ =40.401+71.906+11.981\end{array}$

$=124.288$

Mean sum of squares due to error:

$\begin{array}{c}MSE=\frac{124.28}{n-k-1}\\ =\frac{124.288}{240-3-1}\\ =\frac{124.288}{236}\\ =0.527\end{array}$

Thus, the F-statistic is calculated as follows:

$\begin{array}{c}f=\frac{MS{T}_r}{MSE}\\ =\frac{1.7491}{0.527}\\ =3.319\end{array}$

Critical value:

Software procedure:

Step-by-step procedure to obtain the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 2 in numerator df and 236 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tail.
• Choose Probability as 0.05.
• Click OK.

Output obtained from MINITAB is given below:

Thus, the critical value is 3.034.

Conclusion:

The test statisticis 3.319and the critical value is 3.034.

The test statisticis lesser than the critical value.

That is, $3.319\left(=\text{test statistic}\right)>3.034\left(=\text{critical value}\right)$.

Thus, the null hypothesis is rejected.

Hence, there is sufficient evidence to conclude that there is a difference in the average number of prior non-soccer concussion between the three groups.