
Concept explainers
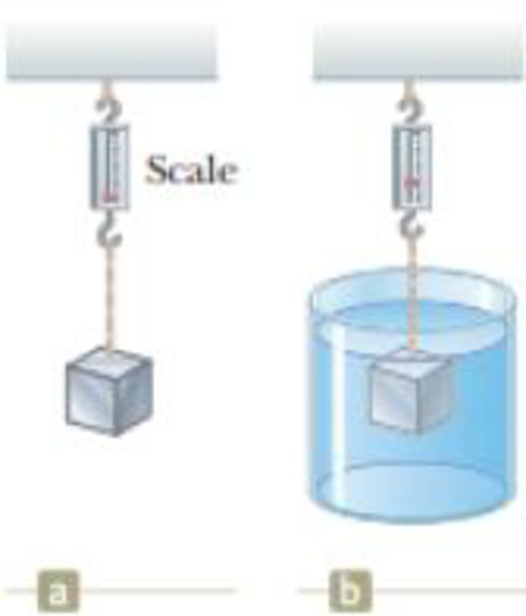
A 10.0-kg block of metal measuring 12.0 cm by 10.0 cm by 10.0 cm is suspended from a scale and immersed in water as shown in Figure P14.11b. The 12.0-cm dimension is vertical, and the top of the block is 5.00 cm below the surface of the water. (a) What are the magnitudes of the forces acting on the top and on the bottom of the block due to the surrounding water? (b) What is the reading of the spring scale? (c) Show that the buoyant force equals the difference between the forces at the top and bottom of the block.
Figure P14.11 Problems 11 and 12.
(a)
The magnitudes of the forces acting on the top and on the bottom of the block due to the surrounding water.
Answer to Problem 27P
The magnitudes of the forces acting on the top and on the bottom of the block due to the surrounding water is
Explanation of Solution
Section 1:
To determine: The magnitudes of the force acting on the top of the block due to the surrounding water.
Answer: The magnitudes of the force acting on the top of the block due to the surrounding water is
Given information:
The mass of the block is
Formula to calculate the absolute pressure at the top of the block is,
Formula to calculate the force acting on the top of the block is,
Substitute
Substitute
Conclusion:
Therefore, the magnitudes of the force acting on the top of the block due to the surrounding water is
Section 2:
To determine: The magnitudes of the force acting on the bottom of the block due to the surrounding water.
Answer: The magnitudes of the force acting on the bottom of the block due to the surrounding water is
Given information:
The mass of the block is
Formula to calculate the absolute pressure at the bottom of the block is,
Formula to calculate the force acting on the bottom of the block is,
Substitute
Substitute
Conclusion:
Therefore, the magnitudes of the force acting on the bottom of the block due to the surrounding water is
(b)
The reading of the spring scale.
Answer to Problem 27P
The reading in the spring scale is
Explanation of Solution
Given information:
The mass of the block is
The scale reading when the block is immersed in water is equal to the tension in the chord supporting the block.
Apply the equilibrium condition.
Rearrange the above equation for
Substitute
Conclusion:
Therefore, the reading in the spring scale is
(c)
To show: That the buoyant force equals the difference between the force at the top and bottom of the block.
Explanation of Solution
Given information:
The mass of the block is
When an object is immersed in a liquid, then the upward force exerted on it by fluid is called buoyant force and its magnitude equals the weight of the liquid displaced by the object.
Formula to calculate the buoyant force is,
Substitute
From part (a), the difference between the force at the top and bottom of the block is,
From the above calculations it is clear that,
Conclusion:
Therefore, the buoyant force equals the difference between the force at the top and bottom of the block.
Want to see more full solutions like this?
Chapter 14 Solutions
Physics For Scientists And Engineers With Modern Physics, 9th Edition, The Ohio State University
- No chatgpt plsarrow_forwardhelp me with the experimental set up for the excel i did. the grapharrow_forwardWhich of the following best describes how to calculate the average acceleration of any object? Average acceleration is always halfway between the initial acceleration of an object and its final acceleration. Average acceleration is always equal to the change in velocity of an object divided by the time interval. Average acceleration is always equal to the displacement of an object divided by the time interval. Average acceleration is always equal to the change in speed of an object divided by the time interval.arrow_forward
- The figure shows the velocity versus time graph for a car driving on a straight road. Which of the following best describes the acceleration of the car? v (m/s) t(s) The acceleration of the car is negative and decreasing. The acceleration of the car is constant. The acceleration of the car is positive and increasing. The acceleration of the car is positive and decreasing. The acceleration of the car is negative and increasing.arrow_forwardWhich figure could represent the velocity versus time graph of a motorcycle whose speed is increasing? v (m/s) v (m/s) t(s) t(s)arrow_forwardUnlike speed, velocity is a the statement? Poisition. Direction. Vector. Scalar. quantity. Which one of the following completesarrow_forward
- No chatgpt pls will upvote Already got wrong chatgpt answerarrow_forward3.63 • Leaping the River II. A physics professor did daredevil stunts in his spare time. His last stunt was an attempt to jump across a river on a motorcycle (Fig. P3.63). The takeoff ramp was inclined at 53.0°, the river was 40.0 m wide, and the far bank was 15.0 m lower than the top of the ramp. The river itself was 100 m below the ramp. Ignore air resistance. (a) What should his speed have been at the top of the ramp to have just made it to the edge of the far bank? (b) If his speed was only half the value found in part (a), where did he land? Figure P3.63 53.0° 100 m 40.0 m→ 15.0 marrow_forwardPlease solve and answer the question correctly please. Thank you!!arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





