Mathematical Ideas (13th Edition) - Standalone book
13th Edition
ISBN: 9780321977076
Author: Charles D. Miller, Vern E. Heeren, John Hornsby, Christopher Heeren
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 14, Problem 1T
Basic Concepts In Exercises 1-5, refer to the following graph.
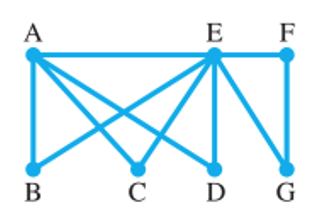
Determine how many vertices the graph has.
Expert Solution & Answer
To determine
The number of vertices in the provided graph.
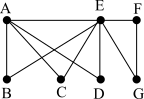
The graph is:
Answer to Problem 1T
Solution:
The number of vertices is
Explanation of Solution
Given:
The graph is:
Explanation:
A graph is a collection of vertices and edges, and each dot is a vertex of the graph.
To determine the number of vertices, count the number of dots. The graph has dots A, B, C, D, G, F and E. In total, there are seven dots. Therefore, the number of vertices in the graph is
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Can you answer this question and give step by step and why and how to get it. Can you write it (numerical method)
Construct tables showing the values of alI the Dirichlet characters mod k fork = 8,9, and 10.
(please show me result in a table and the equation in mathematical format.)
Example: For what odd primes p is 11 a quadratic residue modulo p?
Solution:
This is really asking "when is (11 | p) =1?"
First, 11 = 3 (mod 4). To use LQR, consider two cases p = 1 or 3 (mod 4):
p=1 We have 1 = (11 | p) = (p | 11), so p is a quadratic residue modulo 11. By
brute force:
121, 224, 3² = 9, 4² = 5, 5² = 3 (mod 11)
so the quadratic residues mod 11 are 1,3,4,5,9.
Using CRT for p = 1 (mod 4) & p = 1,3,4,5,9 (mod 11).
p = 1
(mod 4)
&
p = 1
(mod 11
gives p
1
(mod 44).
p = 1
(mod 4)
&
p = 3
(mod 11)
gives p25
(mod 44).
p = 1
(mod 4)
&
p = 4
(mod 11)
gives p=37
(mod 44).
p = 1
(mod 4)
&
p = 5
(mod 11)
gives p
5
(mod 44).
p = 1
(mod 4)
&
p=9
(mod 11)
gives p
9
(mod 44).
So p =1,5,9,25,37 (mod 44).
Chapter 14 Solutions
Mathematical Ideas (13th Edition) - Standalone book
Ch. 14.1 - Vertices and Edges In Exercises 1-6, determine how...Ch. 14.1 - Vertices and Edges In Exercises 1-6, determine how...Ch. 14.1 - Vertices and Edges In Exercises 1-6, determine how...Ch. 14.1 - Prob. 4ECh. 14.1 - Prob. 5ECh. 14.1 - Prob. 6ECh. 14.1 - Prob. 7ECh. 14.1 - Prob. 8ECh. 14.1 - Prob. 9ECh. 14.1 - Prob. 10E
Ch. 14.1 - Prob. 11ECh. 14.1 - Prob. 12ECh. 14.1 - Prob. 13ECh. 14.1 - Prob. 14ECh. 14.1 - Prob. 15ECh. 14.1 - Prob. 16ECh. 14.1 - Prob. 17ECh. 14.1 - Prob. 18ECh. 14.1 - Prob. 19ECh. 14.1 - Prob. 20ECh. 14.1 - Prob. 21ECh. 14.1 - Prob. 22ECh. 14.1 - Prob. 23ECh. 14.1 - Prob. 24ECh. 14.1 - Prob. 25ECh. 14.1 - Number of Edges In Exercises 23-26, use the...Ch. 14.1 - Prob. 27ECh. 14.1 - Prob. 28ECh. 14.1 - Prob. 29ECh. 14.1 - Prob. 30ECh. 14.1 - Prob. 31ECh. 14.1 - Prob. 32ECh. 14.1 - Prob. 33ECh. 14.1 - Prob. 34ECh. 14.1 - Prob. 35ECh. 14.1 - Prob. 36ECh. 14.1 - Prob. 37ECh. 14.1 - Prob. 38ECh. 14.1 - Prob. 39ECh. 14.1 - Prob. 40ECh. 14.1 - Prob. 41ECh. 14.1 - Prob. 42ECh. 14.1 - Prob. 43ECh. 14.1 - 44. Chess Competition Students from two schools...Ch. 14.1 - Prob. 45ECh. 14.1 - Prob. 46ECh. 14.1 - Prob. 47ECh. 14.1 - Number of Handshakes There are seven people at a...Ch. 14.1 - Prob. 49ECh. 14.1 - Prob. 50ECh. 14.1 - Prob. 51ECh. 14.1 - 52. Students in the Same Class Mary, Erin, Sue,...Ch. 14.1 - Here is another theorem about graphs: In any...Ch. 14.1 - Draw two nonisomorphic (simple) graphs with 6...Ch. 14.1 - Explain why the two graphs drawn in Exercise 54...Ch. 14.1 - Analyzing a Cube with a Graph Draw a graph whose...Ch. 14.1 - Prob. 57ECh. 14.1 - Prob. 58ECh. 14.1 - Prob. 59ECh. 14.1 - Prob. 60ECh. 14.1 - Prob. 61ECh. 14.1 - Prob. 62ECh. 14.1 - Prob. 63ECh. 14.1 - Prob. 64ECh. 14.1 - Prob. 65ECh. 14.1 - Prob. 66ECh. 14.1 - Prob. 67ECh. 14.1 - Prob. 68ECh. 14.1 - Prob. 69ECh. 14.1 - Prob. 70ECh. 14.1 - 71. Inviting Colleagues to a Gathering Several of...Ch. 14.1 - Prob. 72ECh. 14.1 - Prob. 73ECh. 14.1 - Prob. 74ECh. 14.1 - Prob. 75ECh. 14.1 - Graph Coloring In Exercises 75 and 76, draw a...Ch. 14.1 - Prob. 77ECh. 14.1 - Prob. 78ECh. 14.1 - Prob. 79ECh. 14.1 - Prob. 80ECh. 14.1 - Prob. 81ECh. 14.1 - Prob. 82ECh. 14.1 - The Six Degrees of Kevin Bacon Use the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin Bacon Use the Web...Ch. 14.1 - The Six Degrees of Kevin Bacon Use the Web...Ch. 14.1 - The Six Degrees of Kevin Bacon Use the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - The Six Degrees of Kevin BaconUse the Web site...Ch. 14.1 - 93. Lines from She Walks in Beauty, by Lord...Ch. 14.1 - 94. Lines from Annabel Lee, by Edgar Allan Poe
It...Ch. 14.1 - Poetry Analysis Graphs may be used to clarify the...Ch. 14.1 - 96. Lines from Sailing to Byzantium, by William...Ch. 14.2 - Euler Circuits. In Exercises 1-3, a graph is shown...Ch. 14.2 - Prob. 2ECh. 14.2 - Euler Circuits In Exercises 1-3, a graph is shown...Ch. 14.2 - Prob. 4ECh. 14.2 - Euler's Theorem In Exercises 4-8, use Eulers...Ch. 14.2 - Prob. 6ECh. 14.2 - Euler's Theorem.In Exercises 4-8, use Eider's...Ch. 14.2 - Prob. 8ECh. 14.2 - Euler's Theorem In Exercises 9 and 10, use Eider's...Ch. 14.2 - Prob. 10ECh. 14.2 - Euler's Theorem In Exercises 11-14, use Eider's...Ch. 14.2 - Prob. 12ECh. 14.2 - Euler's Theorem In Exercises 11-14, use Euler's...Ch. 14.2 - Prob. 14ECh. 14.2 - Floor Tilings In Exercises 15-18, different floor...Ch. 14.2 - Prob. 16ECh. 14.2 - Floor Tilings In Exercises 15-18, different floor...Ch. 14.2 - Prob. 18ECh. 14.2 - Prob. 19ECh. 14.2 - Prob. 20ECh. 14.2 - Prob. 21ECh. 14.2 - Prob. 22ECh. 14.2 - Fleury's Algorithm In Exercises 23-25, a graph is...Ch. 14.2 - Prob. 24ECh. 14.2 - Prob. 25ECh. 14.2 - Prob. 26ECh. 14.2 - Fleury's Algorithm In Exercises 26-28\ use...Ch. 14.2 - Prob. 28ECh. 14.2 - Euler's Theorem and Fleury's Algorithm In...Ch. 14.2 - Euler's Theorem and Fleury's Algorithm In...Ch. 14.2 - Euler's Theorem and Fleury's Algorithm In...Ch. 14.2 - Prob. 32ECh. 14.2 - 33. Parking Pattern The map shows the roads on...Ch. 14.2 - Prob. 34ECh. 14.2 - Floor Plans In Exercises 34-36, the floor plan of...Ch. 14.2 - Prob. 36ECh. 14.2 - Exercises 37-44 are based on the following...Ch. 14.2 - Prob. 38ECh. 14.2 - Exercises 37-44 are based on the following...Ch. 14.2 - Prob. 40ECh. 14.2 - Exercises 37-44 are based on the following...Ch. 14.2 - Floor PlansIn Exercises 41-43, refer to the floor...Ch. 14.2 - Prob. 43ECh. 14.2 - Prob. 44ECh. 14.2 - Prob. 45ECh. 14.2 - Prob. 46ECh. 14.2 - Prob. 47ECh. 14.2 - Prob. 48ECh. 14.2 - Prob. 49ECh. 14.2 - Route Planning For each street grid in Exercise...Ch. 14.2 - Route Planning For each street grid in Exercise...Ch. 14.2 - Route Planning For each street grid in Exercise...Ch. 14.3 - Prob. 1ECh. 14.3 - Prob. 2ECh. 14.3 - Euler and Hamilton Circuits In Exercises 3 and 4,...Ch. 14.3 - Euler and Hamilton Circuits In Exercises 3 and 4,...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Hamilton Circuits In Exercises 5-10, determine...Ch. 14.3 - Prob. 11ECh. 14.3 - Prob. 12ECh. 14.3 - Prob. 13ECh. 14.3 - Decide whether each statement is true or false. If...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - Hamilton and Euler Circuits In Exercises 15-20,...Ch. 14.3 - FactorialsIn Exercises 21-24, use a calculator, if...Ch. 14.3 - Factorials In Exercises 21-24, use a calculator,...Ch. 14.3 - Factorials In Exercises 21-24, use a calculator,...Ch. 14.3 - Prob. 24ECh. 14.3 - Hamilton Circuit In Exercises 25-28, determine how...Ch. 14.3 - Prob. 26ECh. 14.3 - Prob. 27ECh. 14.3 - Prob. 28ECh. 14.3 - List all Hamilton circuits in the graph that start...Ch. 14.3 - Prob. 30ECh. 14.3 - Prob. 31ECh. 14.3 - Prob. 32ECh. 14.3 - Prob. 33ECh. 14.3 - Prob. 34ECh. 14.3 - Prob. 35ECh. 14.3 - Prob. 36ECh. 14.3 - Prob. 37ECh. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Brute Force Algorithm In Exercises 38-41, use the...Ch. 14.3 - Prob. 42ECh. 14.3 - Prob. 43ECh. 14.3 - Nearest Neighbor Algorithm In Exercises 42-44, use...Ch. 14.3 - 45. Nearest Neighbor Algorithm Refer to the...Ch. 14.3 - Prob. 46ECh. 14.3 - Prob. 47ECh. 14.3 - Prob. 48ECh. 14.3 - Prob. 49ECh. 14.3 - Hamilton Circuits In Exercises 47-50, find all...Ch. 14.3 - Traveling Salesman Problem The diagram represents...Ch. 14.3 - Prob. 52ECh. 14.3 - The Icosian Game The graph below shows the Icosian...Ch. 14.3 - Prob. 54ECh. 14.3 - Dirac's Theorem Paul A. M. Dirac proved the...Ch. 14.4 - Prob. 1ECh. 14.4 - Prob. 2ECh. 14.4 - Prob. 3ECh. 14.4 - Prob. 4ECh. 14.4 - Prob. 5ECh. 14.4 - Prob. 6ECh. 14.4 - Prob. 7ECh. 14.4 - Prob. 8ECh. 14.4 - Prob. 9ECh. 14.4 - Prob. 10ECh. 14.4 - Prob. 11ECh. 14.4 - Tree or Not a Tree? In Exercises 11-13, determine...Ch. 14.4 - Prob. 13ECh. 14.4 - Prob. 14ECh. 14.4 - Trees and Cut Edges In Exercises 14-17, determine...Ch. 14.4 - Trees and Cut Edges In Exercises 14-17, determine...Ch. 14.4 - Prob. 17ECh. 14.4 - Prob. 18ECh. 14.4 - Prob. 19ECh. 14.4 - Prob. 20ECh. 14.4 - Prob. 21ECh. 14.4 - Prob. 22ECh. 14.4 - Prob. 23ECh. 14.4 - Prob. 24ECh. 14.4 - Prob. 25ECh. 14.4 - Prob. 26ECh. 14.4 - Prob. 27ECh. 14.4 - Prob. 28ECh. 14.4 - Prob. 29ECh. 14.4 - Prob. 30ECh. 14.4 - Prob. 31ECh. 14.4 - Prob. 32ECh. 14.4 - Prob. 33ECh. 14.4 - Town Water Distribution A town council is planning...Ch. 14.4 - Prob. 35ECh. 14.4 - Prob. 36ECh. 14.4 - Prob. 37ECh. 14.4 - Prob. 38ECh. 14.4 - Prob. 39ECh. 14.4 - For Exercise 34
Trees, Edges, and Vertices Work...Ch. 14.4 - 41. Suppose we have a tree with 10 vertices.
(a)...Ch. 14.4 - Prob. 42ECh. 14.4 - Prob. 43ECh. 14.4 - 44. Design of a Garden Maria has 12 vegetable and...Ch. 14.4 - Prob. 45ECh. 14.4 - Prob. 46ECh. 14.4 - Prob. 47ECh. 14.4 - Prob. 48ECh. 14.4 - Prob. 49ECh. 14.4 - Prob. 50ECh. 14.4 - Prob. 51ECh. 14.4 - Prob. 52ECh. 14.4 - Prob. 53ECh. 14.4 - Prob. 54ECh. 14.4 - Prob. 55ECh. 14.4 - Vertex/Edge Relationship In this exercise, we...Ch. 14 - Basic Concepts In Exercises 1-5, refer to the...Ch. 14 - Basic Concepts In Exercises 1-5, refer to the...Ch. 14 - Prob. 3TCh. 14 - Prob. 4TCh. 14 - Prob. 5TCh. 14 - Prob. 6TCh. 14 - Prob. 7TCh. 14 - Prob. 8TCh. 14 - Planning for Dinner Julia is planning to invite...Ch. 14 - Prob. 10TCh. 14 - Prob. 11TCh. 14 - Prob. 12TCh. 14 - Prob. 13TCh. 14 - Scheduling Exams A teacher at a high school must...Ch. 14 - Prob. 15TCh. 14 - Prob. 16TCh. 14 - Prob. 17TCh. 14 - Prob. 18TCh. 14 - Prob. 19TCh. 14 - Prob. 20TCh. 14 - Prob. 21TCh. 14 - Prob. 22TCh. 14 - Prob. 23TCh. 14 - Prob. 24TCh. 14 - Prob. 25TCh. 14 - 26. Nonisomorphic Trees Draw three nonisomorphic...Ch. 14 - Prob. 27TCh. 14 - Prob. 28TCh. 14 - Prob. 29TCh. 14 - Prob. 30TCh. 14 - Prob. 31TCh. 14 - Prob. 32T
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Can you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forwardJamal wants to save $48,000 for a down payment on a home. How much will he need to invest in an account with 11.8% APR, compounding daily, in order to reach his goal in 10 years? Round to the nearest dollar.arrow_forwardr nt Use the compound interest formula, A (t) = P(1 + 1)". An account is opened with an intial deposit of $7,500 and earns 3.8% interest compounded semi- annually. Round all answers to the nearest dollar. a. What will the account be worth in 10 years? $ b. What if the interest were compounding monthly? $ c. What if the interest were compounded daily (assume 365 days in a year)? $arrow_forward
- Kyoko has $10,000 that she wants to invest. Her bank has several accounts to choose from. Her goal is to have $15,000 by the time she finishes graduate school in 7 years. To the nearest hundredth of a percent, what should her minimum annual interest rate be in order to reach her goal assuming they compound daily? (Hint: solve the compound interest formula for the intrerest rate. Also, assume there are 365 days in a year) %arrow_forwardTest the claim that a student's pulse rate is different when taking a quiz than attending a regular class. The mean pulse rate difference is 2.7 with 10 students. Use a significance level of 0.005. Pulse rate difference(Quiz - Lecture) 2 -1 5 -8 1 20 15 -4 9 -12arrow_forwardThere are three options for investing $1150. The first earns 10% compounded annually, the second earns 10% compounded quarterly, and the third earns 10% compounded continuously. Find equations that model each investment growth and use a graphing utility to graph each model in the same viewing window over a 20-year period. Use the graph to determine which investment yields the highest return after 20 years. What are the differences in earnings among the three investment? STEP 1: The formula for compound interest is A = nt = P(1 + − − ) n², where n is the number of compoundings per year, t is the number of years, r is the interest rate, P is the principal, and A is the amount (balance) after t years. For continuous compounding, the formula reduces to A = Pert Find r and n for each model, and use these values to write A in terms of t for each case. Annual Model r=0.10 A = Y(t) = 1150 (1.10)* n = 1 Quarterly Model r = 0.10 n = 4 A = Q(t) = 1150(1.025) 4t Continuous Model r=0.10 A = C(t) =…arrow_forward
- The following ordered data list shows the data speeds for cell phones used by a telephone company at an airport: A. Calculate the Measures of Central Tendency from the ungrouped data list. B. Group the data in an appropriate frequency table. C. Calculate the Measures of Central Tendency using the table in point B. D. Are there differences in the measurements obtained in A and C? Why (give at least one justified reason)? I leave the answers to A and B to resolve the remaining two. 0.8 1.4 1.8 1.9 3.2 3.6 4.5 4.5 4.6 6.2 6.5 7.7 7.9 9.9 10.2 10.3 10.9 11.1 11.1 11.6 11.8 12.0 13.1 13.5 13.7 14.1 14.2 14.7 15.0 15.1 15.5 15.8 16.0 17.5 18.2 20.2 21.1 21.5 22.2 22.4 23.1 24.5 25.7 28.5 34.6 38.5 43.0 55.6 71.3 77.8 A. Measures of Central Tendency We are to calculate: Mean, Median, Mode The data (already ordered) is: 0.8, 1.4, 1.8, 1.9, 3.2, 3.6, 4.5, 4.5, 4.6, 6.2, 6.5, 7.7, 7.9, 9.9, 10.2, 10.3, 10.9, 11.1, 11.1, 11.6, 11.8, 12.0, 13.1, 13.5, 13.7, 14.1, 14.2, 14.7, 15.0, 15.1, 15.5,…arrow_forwardA tournament is a complete directed graph, for each pair of vertices x, y either (x, y) is an arc or (y, x) is an arc. One can think of this as a round robin tournament, where the vertices represent teams, each pair plays exactly once, with the direction of the arc indicating which team wins. (a) Prove that every tournament has a direct Hamiltonian path. That is a labeling of the teams V1, V2,..., Un so that vi beats Vi+1. That is a labeling so that team 1 beats team 2, team 2 beats team 3, etc. (b) A digraph is strongly connected if there is a directed path from any vertex to any other vertex. Equivalently, there is no partition of the teams into groups A, B so that every team in A beats every team in B. Prove that every strongly connected tournament has a directed Hamiltonian cycle. Use this to show that for any team there is an ordering as in part (a) for which the given team is first. (c) A king in a tournament is a vertex such that there is a direct path of length at most 2 to any…arrow_forwardUse a graphing utility to find the point of intersection, if any, of the graphs of the functions. Round your result to three decimal places. (Enter NONE in any unused answer blanks.) y = 100e0.01x (x, y) = y = 11,250 ×arrow_forward
- how to construct the following same table?arrow_forwardThe following is known. The complete graph K2t on an even number of vertices has a 1- factorization (equivalently, its edges can be colored with 2t - 1 colors so that the edges incident to each vertex are distinct). This implies that the complete graph K2t+1 on an odd number of vertices has a factorization into copies of tK2 + K₁ (a matching plus an isolated vertex). A group of 10 people wants to set up a 45 week tennis schedule playing doubles, each week, the players will form 5 pairs. One of the pairs will not play, the other 4 pairs will each play one doubles match, two of the pairs playing each other and the other two pairs playing each other. Set up a schedule with the following constraints: Each pair of players is a doubles team exactly 4 times; during those 4 matches they see each other player exactly once; no two doubles teams play each other more than once. (a) Find a schedule. Hint - think about breaking the 45 weeks into 9 blocks of 5 weeks. Use factorizations of complete…arrow_forward. The two person game of slither is played on a graph. Players 1 and 2 take turns, building a path in the graph. To start, Player 1 picks a vertex. Player 2 then picks an edge incident to the vertex. Then, starting with Player 1, players alternate turns, picking a vertex not already selected that is adjacent to one of the ends of the path created so far. The first player who cannot select a vertex loses. (This happens when all neighbors of the end vertices of the path are on the path.) Prove that Player 2 has a winning strategy if the graph has a perfect matching and Player 1 has a winning strategy if the graph does not have a perfect matching. In each case describe a strategy for the winning player that guarantees that they will always be able to select a vertex. The strategy will be based on using a maximum matching to decide the next choice, and will, for one of the cases involve using the fact that maximality means no augmenting paths. Warning, the game slither is often described…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY