Chapter 14, Problem 14.1RP

A = 2300 mm², I = 9.5(10⁶) mm⁴.

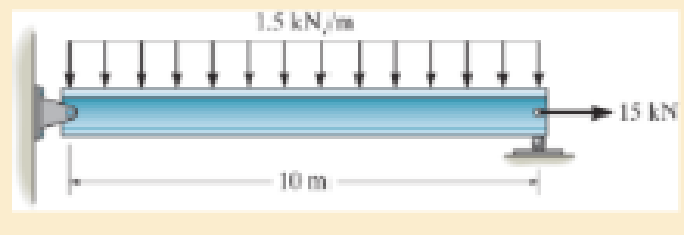
R14–1

To determine

The total axial and bending strain energy in the A992 steel beam.

Answer to Problem 14.1RP

The total axial and bending strain energy in the A992 steel beam is $\underset{\_}{U=496\text{J}}$.

Explanation of Solution

Given information:

The cross-sectional area of the beam is $A=2,300{\text{mm}}^{\text{2}}$.

Moment of inertia of the beam is $I=9.5\times {10}^6{\text{mm}}^4$.

Assumption:

The modulus of elasticity or Young’s modulus of theA992 steelis $E=200\text{GPa}=\text{200}\times {\text{10}}^9{\text{N/m}}^2$.

Explanation:

Determine the reactions:

Entire beam:

Show the free body diagram of the entire beam as in Figure 1.

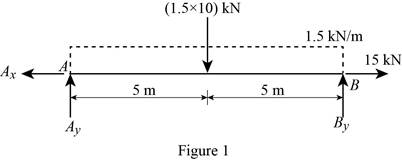
Moment about the point A:

Determine the vertical reaction at point B by taking moment about point A.

$\begin{array}{l}{\displaystyle \sum M_A=0}\\ B_y\left(10\right)-1.5\times 10\times \frac{10}{2}=0\end{array}$ (1)

Along the vertical direction:

Determine the vertical reaction at point B by resolving the vertical component of forces.

$\begin{array}{l}{\displaystyle \sum F_y=0}\\ A_y+B_y-1.5\times 10=0\end{array}$ (2)

Along the horizontal direction:

Determine the horizontal reaction at point A by resolving the horizontal component of force.

$\begin{array}{l}{\displaystyle \sum F_x=0}\\ 15-A_x=0\end{array}$ (3)

Show the calculation of reaction as follows:

Solve Equation (1).

$\begin{array}{l}10B_y-75=0\\ B_y=7.5\text{kN}\end{array}$

Substitute 7.5kN for $B_y$ in Equation (2).

$\begin{array}{l}{A}_y+7.5-15=0\\ A_y=7.5\text{kN}\end{array}$

Solve Equation (3).

$A_x=15\text{kN}$

Region $0\le x\le 10\text{m}$:

Show the free-body diagram of the section as in Figure 2.

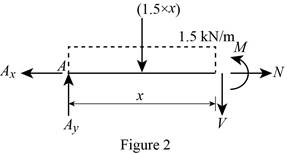
Moment about the section:

Determine the moment at section by taking moment about the section.

$\begin{array}{l}{\displaystyle \sum M_x=0}\\ M+1.5\times x\times \frac{x}{2}-A_y\left(x\right)=0\end{array}$ (4)

Along the horizontal direction:

Determine the normal axial force at the section by resolving the horizontal component of forces.

$\begin{array}{l}{\displaystyle \sum F_x=0}\\ N-A_x=0\end{array}$ (5)

Show the calculation of values as follows:

Substitute 7.5kN for $A_y$ in Equation (4).

$\begin{array}{l}M+0.75x^2-7.5\left(x\right)=0\\ M=7.5x-0.75x^2\end{array}$

Substitute 15 kN for $A_x$ Equation (5).

$\begin{array}{c}N-15=0\\ N=15\text{kN}\end{array}$

Strain energy due to axial load:

Determine the strain energy of a bar of constant cross-sectional area A and constant internal axial load N using the equation.

${\left(U_i\right)}_a=\frac{N^{2}L}{2AE}$ (6)

Here, N is the axial load, L is the length of beam, E is Young’s modulus or modulus of elasticity, and A is cross-sectional area of the beam.

Substitute 15 kN for N, 10 m for L, $2,350{\text{mm}}^2$ for A, and $\text{200}\times {\text{10}}^9{\text{N/m}}^2$ for E in Equation (6).

$\begin{array}{c}{\left(U_i\right)}_a=\frac{{\left(15\text{kN}\times \frac{\text{1,000}\text{N}}{\text{1}\text{kN}}\right)}^2\times 10\text{m}}{2\times 2,300{\text{mm}}^2\times {\left(\frac{\text{1}\text{m}}{\text{1,000}\text{mm}}\right)}^2\times \text{200}\times {\text{10}}^9}\\ =2.4456\text{J}\end{array}$

Strain energy due to Bending:

Determine the strain energy in the beam due to bending using the equation.

${\left(U_i\right)}_b={\displaystyle \underset{0}{\overset{L}{\int }}\frac{M^{2}dx}{2EI}}$ (7)

Here, M is the moment in the beam and I is the moment of inertia of the beam.

Substitute 10 m for L, $\left(7.5x-0.75x^2\right)$ for M, $\text{200}\times {\text{10}}^9{\text{N/m}}^2$ for E, and $9.5\times {10}^6{\text{mm}}^4$ for I in Equation (7), and integrate.

$\begin{array}{c}{\left(U_i\right)}_b={\displaystyle \underset{0}{\overset{10}{\int }}\frac{{\left(7.5x-0.75x^2\right)}^{2}dx}{2\times \text{200}\times {\text{10}}^9\times 9.5\times {10}^6{\text{mm}}^4\times {\left(\frac{\text{1}\text{m}}{\text{1,000}\text{mm}}\right)}^4}}\\ =\frac{1}{2\times \text{200}\times {\text{10}}^9\times 9.5\times {10}^{-6}}{\displaystyle \underset{0}{\overset{10}{\int }}\left(56.25x^2-11.25x^3+0.5625x^4\right)dx}\\ =\frac{1}{2\times \text{200}\times {\text{10}}^9\times 9.5\times {10}^{-6}}{\left[\frac{56.25x^3}{3}-\frac{11.25x^4}{4}+\frac{0.5625x^5}{5}\right]}_0^{10}\\ =\frac{1}{2\times \text{200}\times {\text{10}}^9\times 9.5\times {10}^{-6}}\left[\frac{56.25{\left(10\right)}^3}{3}-\frac{11.25{\left(10\right)}^4}{4}+\frac{0.5625{\left(10\right)}^5}{5}-0+0-0\right]\end{array}$

$\begin{array}{c}=\frac{1,875{\text{kN}}^2\times \frac{\text{1,000}\text{N}}{\text{1}\text{kN}}}{2\times \text{200}\times {\text{10}}^9\times 9.5\times {10}^{-6}}\\ =493.421\text{J}\end{array}$

Total strain energy:

Determine the total strain energy by adding the strain energy due to axial load and the strain energy due to bending.

$U={\left(U_i\right)}_a+{\left(U_i\right)}_b$ (8)

Substitute 2.4456 J for ${\left(U_i\right)}_a$ and 493.421 J for ${\left(U_i\right)}_b$ in Equation (8).

$\begin{array}{c}U=2.4456+493.421\\ =495.87\text{J}\\ \approx 496\text{J}\end{array}$

Thus, the total axial and bending strain energy in the A992 steel beam is $\underset{\_}{U=496\text{J}}$.