
Mathematical Methods in the Physical Sciences
3rd Edition
ISBN: 9780471198260
Author: Mary L. Boas
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 13.4, Problem 4P
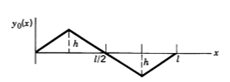
Solve Problem 2 if the initial displacement is :
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Evaluate the triple integral
3'
23
HIG
2
+3
f(x, y, z)dxdydz where f(x, y, z) = x +
2x-y
ม
u =
v =
and w =
2
2
3
Triple Integral
Region R
-2
x
N
2
y
3
Find the volume of the solid bounded below by the circular cone z = 2.5√√√x² + y² and above by the
sphere x² + y²+z² = 6.5z.
Electric charge is distributed over the triangular region D shown below so that the charge density at (x, y)
is σ(x, y) = 4xy, measured in coulumbs per square meter (C/m²). Find the total charge on D. Round
your answer to four decimal places.
1
U
5
4
3
2
1
1
2
5
7
coulumbs
Chapter 13 Solutions
Mathematical Methods in the Physical Sciences
Ch. 13.1 - Assume from electrostatics the equations E=/0 and...Ch. 13.1 - Show that the expression u=sin(xvt) describing a...Ch. 13.1 - Assume from electrodynamics the following...Ch. 13.1 - Obtain the heat flow equation (1.3) as follows:...Ch. 13.2 - After you find the series solution of a problem,...Ch. 13.2 - T=0,0x10,100,10x20. Solve the semi-infinite plate...Ch. 13.2 - Solve the semi-infinite plate problem if the...Ch. 13.2 - Solve the semi-infinite plate problem if the...Ch. 13.2 - Show that the solutions of (2.5) can also be...Ch. 13.2 - Show that the series in (2.12) can be summed to...
Ch. 13.2 - Solve Problem 3 if the plate is cut off at height...Ch. 13.2 - Find the steady-state temperature distribution in...Ch. 13.2 - Solve Problem 2 if the plate is cut off at height...Ch. 13.2 - Find the steady-state temperature distribution in...Ch. 13.2 - Find the steady-state temperature distribution in...Ch. 13.2 - Find the temperature distribution in a rectangular...Ch. 13.2 - Find the steady-state temperature distribution in...Ch. 13.2 - In the rectangular plate problem, we have so far...Ch. 13.2 - Consider a finite plate, 10cm by 30cm, with two...Ch. 13.2 - Show that there is only one function u which...Ch. 13.3 - Verify the coefficients in equation (3.14).Ch. 13.3 - A bar 10 cm long with insulated sides is initially...Ch. 13.3 - In the initial steady state of an infinite slab of...Ch. 13.3 - At t=0, two flat slabs each 5cm thick, one at 0...Ch. 13.3 - Prob. 5PCh. 13.3 - Show that the following problem is easily solved...Ch. 13.3 - A bar of length l with insulated sides has its...Ch. 13.3 - A bar of length 2 is initially at 0. From t=0 on,...Ch. 13.3 - Solve Problem 8 if, for t0, the x=0 end of the bar...Ch. 13.3 - Separate the wave equation (1.4) into a space...Ch. 13.3 - Solve the particle in a box problem to find (x,t)...Ch. 13.3 - Do Problem 11 if (x,0)=sin2x on (0,1).Ch. 13.4 - Complete the plucked string problem to get...Ch. 13.4 - A string of length l has a zero initial velocity...Ch. 13.4 - Solve Problem 2 if the initial displacement is:Ch. 13.4 - Solve Problem 2 if the initial displacement is :Ch. 13.4 - A string of length l is initially stretched...Ch. 13.4 - Do Problem 5 if the initial velocity V(x)=(y/t)t=0...Ch. 13.4 - Solve Problem 5 if the initial velocity is:Ch. 13.4 - Solve Problem 5 if the initial velocity is...Ch. 13.4 - In each of the Problems 1 to 8,find the frequency...Ch. 13.4 - Verify that, if k=nT, then the sum of the two...Ch. 13.4 - Verify (4.16) and find a similar formula for a...Ch. 13.4 - In Sections 2, 3, 4, we have solved a number of...Ch. 13.4 - Do Problem 12 for f(x)=1cos2x on (0,).Ch. 13.4 - Do Problem 12 for f(x)=xx3 on (0, 1).Ch. 13.5 - Compute numerically the coefficients (5.16) of the...Ch. 13.5 - Find the steady-state temperature distribution in...Ch. 13.5 - Find the steady-state temperature distribution in...Ch. 13.5 - A flat circular plate of radius a is initially at...Ch. 13.5 - Do Problem 4 if the initial temperature...Ch. 13.5 - Consider Problem 4 if the initial temperature...Ch. 13.5 - Find the steady-state temperature distribution in...Ch. 13.5 - Water at 100 is flowing through a long pipe of...Ch. 13.5 - Find the steady-state distribution of temperature...Ch. 13.5 - A cube is originally at 100. From t=0 on, the...Ch. 13.5 - The following two R(r) equations arise in various...Ch. 13.5 - Separate Laplaces equation in two dimensions in...Ch. 13.5 - Find the steady-state distribution of temperature...Ch. 13.5 - Find the steady state temperature distribution in...Ch. 13.5 - Solve Problem 14 if the temperatures of the two...Ch. 13.6 - Continue Figure 6.1 to show the fundamental modes...Ch. 13.6 - Prob. 2PCh. 13.6 - Separate the wave equation in two-dimensional...Ch. 13.6 - Find the characteristic frequencies for sound...Ch. 13.6 - A square membrane of side l is distorted into the...Ch. 13.6 - Let V=0 in the Schrödinger equation (3.22) and...Ch. 13.6 - In your Problem 6 solutions, find some examples of...Ch. 13.6 - Do Problem 6 in polar coordinates to find the...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Do Problem 11 if the curved surface is held at...Ch. 13.7 - Find the electrostatic potential outside a...Ch. 13.7 - Find the steady-state temperature distribution in...Ch. 13.7 - A sphere initially at 0 has its surface kept at...Ch. 13.7 - Separate the wave equation in spherical...Ch. 13.7 - Do Problem 6.6 in 3 dimensional rectangular...Ch. 13.7 - Prob. 18PCh. 13.7 - Find the eigenfunctions and energy eigenvalues for...Ch. 13.7 - Write the Schrödinger equation (3.22) if is a...Ch. 13.7 - Prob. 21PCh. 13.7 - Find the energy eigenvalues and eigen functions...Ch. 13.8 - Show that the gravitational potential V=Gm/r...Ch. 13.8 - Using the formulas of Chapter 12, Section 5, sum...Ch. 13.8 - Do the problem in Example 1 for the case of a...Ch. 13.8 - Prob. 4PCh. 13.8 - Find the method of images for problem 4.Ch. 13.8 - Substitute (8.25) into (8.22) and use (8.23) and...Ch. 13.8 - Verify that the Green function in (8.29) is zero...Ch. 13.8 - Show that the Green function (8.28) which is zero...Ch. 13.8 - Show that our results can be extended to find the...Ch. 13.9 - Verify that (9.15) follows from (9.14). Hint: Use...Ch. 13.9 - A metal plate covering the first quadrant has the...Ch. 13.9 - Consider the heat flow problem of Section 3. Solve...Ch. 13.9 - A semi-infinite bar is initially at temperature...Ch. 13.9 - Prob. 5PCh. 13.9 - Continue the problem of Example 2 in the following...Ch. 13.9 - Continue with Problem 4 as in Problem 6.Ch. 13.10 - Find the steady-state temperature distribution in...Ch. 13.10 - Solve Problem 1 if T=0 for x=0,x=1,y=0, and T=1x...Ch. 13.10 - Solve Problem 1 if the sides x=0 and x=1 are...Ch. 13.10 - Find the steady-state temperature distribution in...Ch. 13.10 - A bar of length l is initially at 0. From t=0 on,...Ch. 13.10 - Do Problem 5 if the x=0 end is insulated and the...Ch. 13.10 - Solve Problem 2 if the sides x=0 and x=1 are...Ch. 13.10 - A slab of thickness 10cm has its two faces at 10...Ch. 13.10 - A string of length l has initial displacement...Ch. 13.10 - Solve Problem 5.7 if half the curved surface of...Ch. 13.10 - The series in Problem 5.12 can be summed (see...Ch. 13.10 - A plate in the shape of a quarter circle has...Ch. 13.10 - Sum the series in Problem 12 to get...Ch. 13.10 - A long cylinder has been cut into quarter...Ch. 13.10 - Repeat Problems 12 and 13 for a plate in the shape...Ch. 13.10 - Consider the normal modes of vibration for a...Ch. 13.10 - Sketch some of the normal modes of vibration for a...Ch. 13.10 - Repeat Problem 17 for a membrane in the shape of a...Ch. 13.10 - Prob. 19MPCh. 13.10 - Use Problem 7.16 to find the characteristic...Ch. 13.10 - The surface temperature of a sphere of radius 1 is...Ch. 13.10 - Find the interior temperature in a hemisphere if...Ch. 13.10 - Find the steady-state temperature in the region...Ch. 13.10 - Find the general solution for the steady-state...Ch. 13.10 - The Klein-Gordon equation is 2u=1/v22u/t2+2u. This...Ch. 13.10 - Prob. 26MPCh. 13.10 - Do Problem 26 for a rectangular membrane.Ch. 13.10 - Find the steady-state temperature in a...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Fill in each blank so that the resulting statement is true.
1. A combination of numbers, variables, and opera...
College Algebra (7th Edition)
Implicit differentiation Use implicit differentiation to find dydx. 13. sin xy = x + y
Calculus: Early Transcendentals (2nd Edition)
CHECK POINT I You deposit $1000 in a saving account at a bank that has a rate of 4%. a. Find the amount, A, of ...
Thinking Mathematically (6th Edition)
Show that 34=12 using each of the following models. a. Repeated-addition number line b. Rectangular array c. Ar...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Let E be the region bounded cone z = √√/6 - (x² + y²) and the sphere z = x² + y² + z² . Provide an answer accurate to at least 4 significant digits. Find the volume of E. Triple Integral Spherical Coordinates Cutout of sphere is for visual purposes 0.8- 0.6 z 04 0.2- 0- -0.4 -0.2 04 0 0.2 0.2 x -0.2 04 -0.4 Note: The graph is an example. The scale and equation parameters may not be the same for your particular problem. Round your answer to 4 decimal places. Hint: Solve the cone equation for phi. * Oops - try again.arrow_forwardThe temperature at a point (x,y,z) of a solid E bounded by the coordinate planes and the plane 9.x+y+z = 1 is T(x, y, z) = (xy + 8z +20) degrees Celcius. Find the average temperature over the solid. (Answer to 4 decimal places). Average Value of a function using 3 variables z 1- y Hint: y = -a·x+1 * Oops - try again. xarrow_forwardFind the saddle pointsarrow_forward
- Problem #5 Section A of my math class has 110 students. Section B of my math class has 80 students. a). If I randomly select 15 students from the combined classes, in a way that the order of my selection does not matter, what is the probability that all 15 students can from Section A? b). If I randomly select 15 students from the combined classes, in a way that the order of my selection does not matter, what is the probability that all 15 students can from Section B? c). If I randomly select 15 students from the combined classes, in a way that the order of my selection does not matter, what is the probability that all 7 students come from section A and 8 students come from section B?arrow_forwardProblem #6 A special passcode to unlock your phone consists of 4 digits where repeated digits are not allowed. If someone were to randomly guess a 4 digit passcode, what is the probability that they guess your passcode on the first try?arrow_forwardProblem #3 If a card is picked at random from a standard 52-card deck, what is the probability of getting a black card or a queen?arrow_forward
- Problem #1 In the 2010 census, it was reported that the United States had a population of 310 million people. Of those, 74 million were under the age of 18. If you chose a person from the U.S. population at random, what is the probability they are under the age of 18? Problem #2 Given a set S={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, if you were choosing a number at random what is the probability that you would choose an even number or a number larger than 7?arrow_forwardAnswer number twoarrow_forwardAnswer number onearrow_forward
- For the curve defined by r(t) = (e** cos(t), et sin(t)) find the unit tangent vector, unit normal vector, normal acceleration, and tangential acceleration at t = πT 3 T (1) N Ň (1) 133 | aN = 53 ar = = =arrow_forwardFind the tangential and normal components of the acceleration vector for the curve - F(t) = (2t, −3t³, −3+¹) at the point t = 1 - ā(1) = T + Ñ Give your answers to two decimal placesarrow_forwardFind the unit tangent vector to the curve defined by (t)=(-2t,-4t, √√49 - t²) at t = −6. T(−6) =arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY