ELEMENTARY STATS. 18 WEEK ACCESS CODE
13th Edition
ISBN: 9780135900826
Author: Triola
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 13.4, Problem 14BB
Finding Critical Values Assume that we have two treatments (A and B) that produce quantitative results, and we have only two observations for treatment A and two observations for treatment B. We cannot use the Wilcoxon signed ranks test given in this section because both
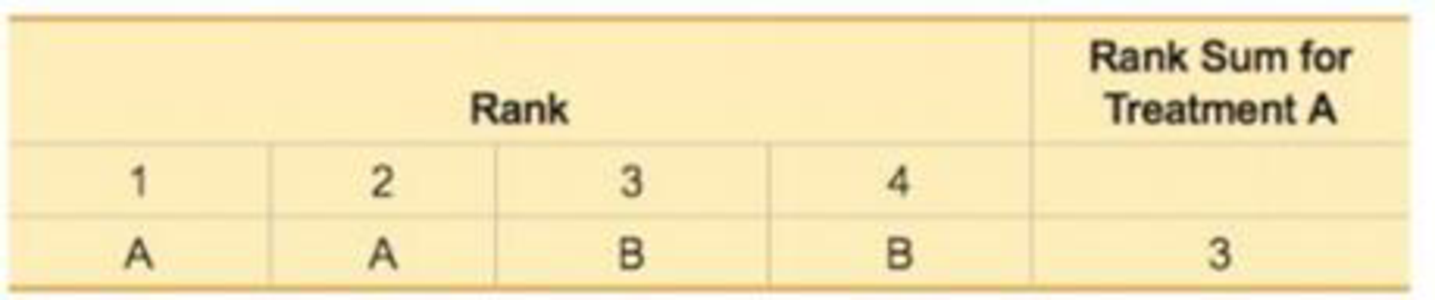
a. Complete the accompanying table by listing the five rows corresponding to the other five possible outcomes, and enter the corresponding rank sums for treatment A.
b. List the possible values of R and their corresponding
c. Is it possible, at the 0.10 significance level, to reject the null hypothesis that there is no difference between treatments A and B? Explain.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
During busy political seasons, many opinion polls are conducted. In apresidential race, how do you think the participants in polls are generally selected?Discuss any issues regarding simple random, stratified, systematic, cluster, andconvenience sampling in these polls. What about other types of polls, besides political?
Please could you explain why 0.5 was added to each upper limpit of the intervals.Thanks
28. (a) Under what conditions do we say that two random variables X and Y are
independent?
(b) Demonstrate that if X and Y are independent, then it follows that E(XY) =
E(X)E(Y);
(e) Show by a counter example that the converse of (ii) is not necessarily true.
Chapter 13 Solutions
ELEMENTARY STATS. 18 WEEK ACCESS CODE
Ch. 13.2 - Prob. 1BSCCh. 13.2 - Prob. 2BSCCh. 13.2 - Contradicting H1 An important step in conducting...Ch. 13.2 - Efficiency of the Sign Test Refer to Table 13-2 on...Ch. 13.2 - Matched Pairs. In Exercises 58, use the sign test...Ch. 13.2 - Matched Pairs. In Exercises 58, use the sign test...Ch. 13.2 - Matched Pairs. In Exercises 58, use the sign test...Ch. 13.2 - Matched Pairs. In Exercises 58, use the sign test...Ch. 13.2 - Nominal Data. In Exercises 912, use the sign test...Ch. 13.2 - Nominal Data. In Exercises 912, use the sign test...
Ch. 13.2 - Nominal Data. In Exercises 912, use the sign test...Ch. 13.2 - Nominal Data. In Exercises 912, use the sign test...Ch. 13.2 - Appendix B Data Sets. In Exercises 1316, refer to...Ch. 13.2 - Appendix B Data Sets. In Exercises 1316, refer to...Ch. 13.2 - Appendix B Data Sets. In Exercises 1316, refer to...Ch. 13.2 - Appendix B Data Sets. In Exercises 1316, refer to...Ch. 13.2 - Procedures for Handling Ties In the sign lest...Ch. 13.2 - Finding Critical Values Table A-7 lists critical...Ch. 13.3 - Wilcoxon Signed-Ranks Test for Body Temperatures...Ch. 13.3 - Prob. 2BSCCh. 13.3 - Prob. 3BSCCh. 13.3 - Prob. 4BSCCh. 13.3 - Using the Wilcoxon Signed-Ranks Test. In Exercises...Ch. 13.3 - Using the Wilcoxon Signed-Ranks Test. In Exercises...Ch. 13.3 - Using the Wilcoxon Signed-Ranks Test. In Exercises...Ch. 13.3 - Using the Wilcoxon Signed-Ranks Test. In Exercises...Ch. 13.3 - Prob. 9BSCCh. 13.3 - Prob. 10BSCCh. 13.3 - Prob. 11BSCCh. 13.3 - Prob. 12BSCCh. 13.3 - Rank Sums Exercise 12 uses Data Set 23 Old...Ch. 13.4 - Prob. 1BSCCh. 13.4 - Rank Sum After ranking the combined list of...Ch. 13.4 - Prob. 3BSCCh. 13.4 - Prob. 4BSCCh. 13.4 - Wilcoxon Rank-Sum Test. In Exercises 58, use the...Ch. 13.4 - Wilcoxon Rank-Sum Test. In Exercises 58, use the...Ch. 13.4 - Wilcoxon Rank-Sum Test. In Exercises 58, use the...Ch. 13.4 - Wilcoxon Rank-Sum Test. In Exercises 58, use the...Ch. 13.4 - Prob. 9BSCCh. 13.4 - Appendix B Data Sets. In Exercises 912, refer to...Ch. 13.4 - Appendix B Data Sets. In Exercises 912, refer to...Ch. 13.4 - Appendix B Data Sets. In Exercises 912, refer to...Ch. 13.4 - Prob. 13BBCh. 13.4 - Finding Critical Values Assume that we have two...Ch. 13.5 - Prob. 1BSCCh. 13.5 - Requirements Assume that we want to use the data...Ch. 13.5 - Notation For the data given in Exercise 1,...Ch. 13.5 - Efficiency Refer to Table 13-2 on page 600 and...Ch. 13.5 - Prob. 5BSCCh. 13.5 - Prob. 6BSCCh. 13.5 - Prob. 7BSCCh. 13.5 - Prob. 8BSCCh. 13.5 - Appendix B Data Sets. In Exercises 912, use the...Ch. 13.5 - Prob. 10BSCCh. 13.5 - Appendix B Data Sets. In Exercises 912, use the...Ch. 13.5 - Appendix B Data Sets. In Exercises 912, use the...Ch. 13.5 - Correcting the H Test Statistic for Ties In using...Ch. 13.6 - Regression If the methods of this section are used...Ch. 13.6 - Level of Measurement Which of the levels of...Ch. 13.6 - Notation What do r, rs , and ps denote? Why is the...Ch. 13.6 - Prob. 4BSCCh. 13.6 - In Exercises 5 and 6, use the scatterplot to find...Ch. 13.6 - In Exercises 5 and 6, use the scatterplot to find...Ch. 13.6 - Testing for Rank Correlation. In Exercises 712,...Ch. 13.6 - Prob. 8BSCCh. 13.6 - Testing for Rank Correlation. In Exercises 712,...Ch. 13.6 - Testing for Rank Correlation. In Exercises 712,...Ch. 13.6 - Prob. 11BSCCh. 13.6 - Testing for Rank Correlation. In Exercises 712,...Ch. 13.6 - Prob. 13BSCCh. 13.6 - Appendix B Data Sets. In Exercises 1316, use the...Ch. 13.6 - Appendix B Data Sets. In Exercises 1316, use the...Ch. 13.6 - Prob. 16BSCCh. 13.6 - Prob. 17BBCh. 13.7 - In Exercises 14, use the following sequence of...Ch. 13.7 - Prob. 2BSCCh. 13.7 - Prob. 3BSCCh. 13.7 - Prob. 4BSCCh. 13.7 - Using the Runs Test for Randomness. In Exercises...Ch. 13.7 - Prob. 6BSCCh. 13.7 - Prob. 7BSCCh. 13.7 - Using the Runs Test for Randomness. In Exercises...Ch. 13.7 - Prob. 9BSCCh. 13.7 - Prob. 10BSCCh. 13.7 - Runs Test with Large Samples. In Exercises 912,...Ch. 13.7 - Prob. 12BSCCh. 13 - Prob. 1CQQCh. 13 - Prob. 2CQQCh. 13 - Prob. 3CQQCh. 13 - Prob. 4CQQCh. 13 - Prob. 5CQQCh. 13 - Prob. 6CQQCh. 13 - Prob. 7CQQCh. 13 - Prob. 8CQQCh. 13 - Prob. 9CQQCh. 13 - Which Test? Three different judges give the same...Ch. 13 - Prob. 1RECh. 13 - Using Nonparametric Tests. In Exercises 110, use a...Ch. 13 - Prob. 3RECh. 13 - Prob. 4RECh. 13 - Prob. 5RECh. 13 - Prob. 6RECh. 13 - Using Nonparametric Tests. In Exercises 110, use a...Ch. 13 - Prob. 8RECh. 13 - Using Nonparametric Tests. In Exercises 1-10, use...Ch. 13 - Prob. 10RECh. 13 - Prob. 1CRECh. 13 - Prob. 2CRECh. 13 - In Exercises 13, use the data listed below. The...Ch. 13 - Prob. 4CRECh. 13 - Prob. 5CRECh. 13 - Prob. 6CRECh. 13 - Prob. 7CRECh. 13 - Prob. 8CRECh. 13 - Fear of Heights Among readers of a USA Today...Ch. 13 - Cell Phones and Crashes: Analyzing Newspaper...Ch. 13 - Prob. 1TPCh. 13 - Prob. 1FDD
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- 19. Let X be a non-negative random variable. Show that lim nE (IX >n)) = 0. E lim (x)-0. = >arrow_forward(c) Utilize Fubini's Theorem to demonstrate that E(X)= = (1- F(x))dx.arrow_forward(c) Describe the positive and negative parts of a random variable. How is the integral defined for a general random variable using these components?arrow_forward
- 26. (a) Provide an example where X, X but E(X,) does not converge to E(X).arrow_forward(b) Demonstrate that if X and Y are independent, then it follows that E(XY) E(X)E(Y);arrow_forward(d) Under what conditions do we say that a random variable X is integrable, specifically when (i) X is a non-negative random variable and (ii) when X is a general random variable?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Hypothesis Testing using Confidence Interval Approach; Author: BUM2413 Applied Statistics UMP;https://www.youtube.com/watch?v=Hq1l3e9pLyY;License: Standard YouTube License, CC-BY
Hypothesis Testing - Difference of Two Means - Student's -Distribution & Normal Distribution; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=UcZwyzwWU7o;License: Standard Youtube License