Calculus: Early Transcendentals, 2nd Edition
Calculus: Early Transcendentals, 2nd Edition
2nd Edition
ISBN: 9780321965165
Author: William L. Briggs, Lyle Cochran, Bernard Gillett
Publisher: PEARSON
bartleby

Concept explainers

Continuous Probability Distributions
Probability distributions are of two types, which are continuous probability distributions and discrete probability distributions. A continuous probability distribution contains an infinite number of values. For example, if time is infinite: you could co…
Normal Distribution
Suppose we had to design a bathroom weighing scale, how would we decide what should be the range of the weighing machine? Would we take the highest recorded human weight in history and use that as the upper limit for our weighing scale? This may not be a…
bartleby

Videos

Textbook Question
Book Icon
Chapter 13.3, Problem 29E

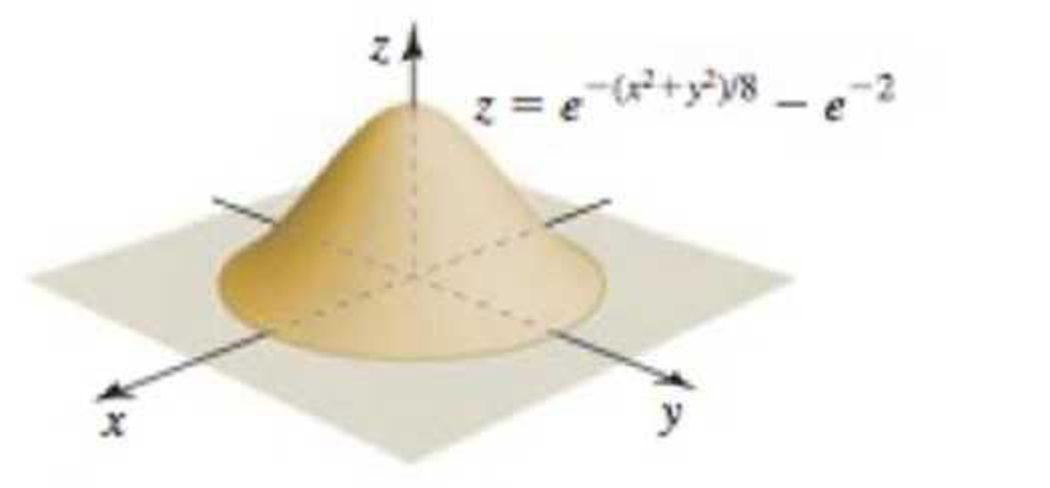
Island problems The surface of an island is defined by the following functions over the region on which the function is nonnegative. Find the volume of the island.

29.     z = e − ( x 2 + y 2 ) / 8 − e − 2

Chapter 13.3, Problem 29E, Island problems The surface of an island is defined by the following functions over the region on

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 13.3, Problem 28E
Next
Chapter 13.3, Problem 30E
Students have asked these similar questions
For what value of A and B the function f(x) will be continuous everywhere for the given definition?..
2. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.4.006.MI. Use the Table of Integrals to evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) 7y2 y² 11 dy Need Help? Read It Master It SUBMIT ANSWER 3. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.4.009. Use the Table of Integrals to evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) tan³(12/z) dz Need Help? Read It Watch It SUBMIT ANSWER 4. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.4.014. Use the Table of Integrals to evaluate the integral. (Use C for the constant of integration.) 5 sinб12x dx Need Help? Read It
Please refer below

Chapter 13 Solutions

Calculus: Early Transcendentals, 2nd Edition

Ch. 13.1 - 1. Write an iterated integral that gives the...Ch. 13.1 - Write an iterated integral that gives the volume...Ch. 13.1 - Write two iterated integrals that equal Rf(x,y)dA,...Ch. 13.1 - Consider the integral 1311(2y2+xy)dydx. State the...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...
Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Prob. 12ECh. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Prob. 20ECh. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Average value Compute the average value of the...Ch. 13.1 - Average value Compute the average value of the...Ch. 13.1 - Average value Compute the average value of the...Ch. 13.1 - Average value 35.Find the average squared distance...Ch. 13.1 - Average value 35.Find the average squared distance...Ch. 13.1 - Explain why or why not Determine whether the...Ch. 13.1 - Symmetry Evaluate the following integrals using...Ch. 13.1 - Computing populations The population densities in...Ch. 13.1 - Prob. 40ECh. 13.1 - Pictures of solids Draw the solid whose volume is...Ch. 13.1 - Prob. 42ECh. 13.1 - More integration practice Evaluate the following...Ch. 13.1 - More integration practice Evaluate the following...Ch. 13.1 - More integration practice Evaluate the following...Ch. 13.1 - More integration practice Evaluate the following...Ch. 13.1 - Volumes of solids Find the volume of the following...Ch. 13.1 - Prob. 48ECh. 13.1 - Volumes of solids Find the volume of the following...Ch. 13.1 - Prob. 50ECh. 13.1 - Solving for a parameter Let R={x,y}:{0x,0ya}. For...Ch. 13.1 - Prob. 52ECh. 13.1 - Zero average value Find the value of a 0 such...Ch. 13.1 - Prob. 54ECh. 13.1 - Density and mass Suppose a thin rectangular plate,...Ch. 13.1 - Approximating volume Propose a method based on...Ch. 13.1 - Cylinders Let S be the solid in 3between the...Ch. 13.1 - Product of integrals Suppose f(x, y) = g(x)h(y),...Ch. 13.1 - Prob. 59ECh. 13.1 - Prob. 60ECh. 13.1 - A generalization Let R be as in Exercise 60, let F...Ch. 13.2 - Describe and sketch a region that is bounded above...Ch. 13.2 - Describe and a sketch a region that is bounded on...Ch. 13.2 - Which order of integration is preferable to...Ch. 13.2 - Which order of integration would you use to find...Ch. 13.2 - Change the order of integration in the integral...Ch. 13.2 - Sketch the region of integration for 22x24exydydxCh. 13.2 - Regions of integration Consider the regions R...Ch. 13.2 - Regions of integration Consider the regions R...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Prob. 20ECh. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Prob. 22ECh. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Regions of integration Write an iterated integral...Ch. 13.2 - Regions of integration Write an iterated integral...Ch. 13.2 - Prob. 33ECh. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Prob. 37ECh. 13.2 - Prob. 38ECh. 13.2 - Prob. 39ECh. 13.2 - Prob. 40ECh. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Prob. 42ECh. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Prob. 52ECh. 13.2 - Volumes Use double integrals to calculate the...Ch. 13.2 - Volumes Use double integrals to calculate the...Ch. 13.2 - Volumes Use double integrals to calculate the...Ch. 13.2 - Prob. 56ECh. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Prob. 63ECh. 13.2 - Changing order of integration The following...Ch. 13.2 - Prob. 65ECh. 13.2 - Changing order of integration The following...Ch. 13.2 - Prob. 67ECh. 13.2 - Changing order of integration The following...Ch. 13.2 - Regions between surfaces Find the volume of the...Ch. 13.2 - Prob. 70ECh. 13.2 - Regions between surfaces Find the volume of the...Ch. 13.2 - Regions between surfaces Find the volume of the...Ch. 13.2 - Regions between surfaces Find the volume of the...Ch. 13.2 - Regions between surfaces Find the volume of the...Ch. 13.2 - Prob. 75ECh. 13.2 - Prob. 76ECh. 13.2 - Prob. 77ECh. 13.2 - Prob. 78ECh. 13.2 - Prob. 79ECh. 13.2 - Prob. 80ECh. 13.2 - Explain why or why not Determine whether the...Ch. 13.2 - Prob. 82ECh. 13.2 - Prob. 83ECh. 13.2 - Prob. 84ECh. 13.2 - Prob. 85ECh. 13.2 - Prob. 86ECh. 13.2 - Two integrals to one Draw the regions of...Ch. 13.2 - Square region Consider the region R = {(x, y): |x|...Ch. 13.2 - Prob. 89ECh. 13.2 - Prob. 90ECh. 13.2 - Area integrals Consider the following regions R....Ch. 13.2 - Area integrals Consider the following regions R....Ch. 13.2 - Prob. 93ECh. 13.2 - Prob. 94ECh. 13.2 - Prob. 95ECh. 13.2 - Prob. 96ECh. 13.2 - Volumes Compute the volume of the following...Ch. 13.2 - Prob. 99ECh. 13.2 - Prob. 100ECh. 13.2 - Prob. 101ECh. 13.2 - Prob. 102ECh. 13.2 - Prob. 103ECh. 13.3 - Draw the region {(r, ): 1 r 2, 0 /2}. Why is...Ch. 13.3 - Write the double integral Rf(x,y)dAas an iterated...Ch. 13.3 - Sketch the region of integration for the integral...Ch. 13.3 - Prob. 4ECh. 13.3 - How do you find the area of a region R = {(r, ):...Ch. 13.3 - How do you find the average value of a function...Ch. 13.3 - Polar rectangles Sketch the following polar...Ch. 13.3 - Polar rectangles Sketch the following polar...Ch. 13.3 - Polar rectangles Sketch the following polar...Ch. 13.3 - Polar rectangles Sketch the following polar...Ch. 13.3 - Solids bounded by paraboloids Find the volume of...Ch. 13.3 - Solids bounded by paraboloids Find the volume of...Ch. 13.3 - Solids bounded by paraboloids Find the volume of...Ch. 13.3 - Solids bounded by paraboloids Find the volume of...Ch. 13.3 - Solids bounded by hyperboloids Find the volume of...Ch. 13.3 - Solids bounded by hyperboloids Find the volume of...Ch. 13.3 - Solids bounded by hyperboloids Find the volume of...Ch. 13.3 - Solids bounded by hyperboloids Find the volume of...Ch. 13.3 - Volume between surfaces Find the volume of the...Ch. 13.3 - Volume between surfaces Find the volume of the...Ch. 13.3 - Volume between surfaces Find the volume of the...Ch. 13.3 - Prob. 22ECh. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Island problems The surface of an island is...Ch. 13.3 - Island problems The surface of an island is...Ch. 13.3 - Island problems The surface of an island is...Ch. 13.3 - Prob. 32ECh. 13.3 - Describing general regions Sketch the following...Ch. 13.3 - Prob. 34ECh. 13.3 - Describing general regions Sketch the following...Ch. 13.3 - Describing general regions Sketch the following...Ch. 13.3 - Describing general regions Sketch the following...Ch. 13.3 - Describing general regions Sketch the following...Ch. 13.3 - Computing areas Sketch each region and use a...Ch. 13.3 - Computing areas Sketch each region and use a...Ch. 13.3 - Computing areas Sketch each region and use a...Ch. 13.3 - Computing areas Sketch each region and use a...Ch. 13.3 - Computing areas Sketch each region and use a...Ch. 13.3 - Prob. 44ECh. 13.3 - Average values Find the following average values....Ch. 13.3 - Prob. 46ECh. 13.3 - Prob. 47ECh. 13.3 - Average values Find the following average values....Ch. 13.3 - Explain why or why not Determine whether the...Ch. 13.3 - Prob. 50ECh. 13.3 - Miscellaneous integrals Evaluate the following...Ch. 13.3 - Miscellaneous integrals Evaluate the following...Ch. 13.3 - Miscellaneous integrals Evaluate the following...Ch. 13.3 - Prob. 54ECh. 13.3 - Prob. 55ECh. 13.3 - Miscellaneous integrals Evaluate the following...Ch. 13.3 - Miscellaneous integrals Evaluate the following...Ch. 13.3 - Areas of circles Use integration to show that the...Ch. 13.3 - Filling bowls with water Which bowl holds more...Ch. 13.3 - Prob. 60ECh. 13.3 - Volume of a hyperbolic paraboloid Consider the...Ch. 13.3 - Prob. 62ECh. 13.3 - Improper integrals Improper integrals arise in...Ch. 13.3 - Improper integrals Improper integrals arise in...Ch. 13.3 - Improper integrals Improper integrals arise in...Ch. 13.3 - Improper integrals Improper integrals arise in...Ch. 13.3 - Prob. 67ECh. 13.3 - Mass from density data The following table gives...Ch. 13.3 - A mass calculation Suppose the density of a thin...Ch. 13.3 - Prob. 70ECh. 13.3 - Prob. 71ECh. 13.3 - Existence of integrals For what values of p does...Ch. 13.3 - Integrals in strips Consider the integral...Ch. 13.3 - Prob. 74ECh. 13.4 - Sketch the region D = {(x, y, z): x2 + y2 4, 0 z...Ch. 13.4 - Write an iterated integral for Df(x,y,z)dV, where...Ch. 13.4 - Write an iterated integral for Df(x,y,z)dV, where...Ch. 13.4 - Sketch the region of integration for the integral...Ch. 13.4 - Write the integral in Exercise 4 in the order dy...Ch. 13.4 - Write an integral for the average value of f(x, y,...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Prob. 34ECh. 13.4 - Finding an appropriate order of integration Find...Ch. 13.4 - Finding an appropriate order of integration Find...Ch. 13.4 - Finding an appropriate order of integration Find...Ch. 13.4 - Finding an appropriate order of integration Find...Ch. 13.4 - Changing the order of integration Rewrite the...Ch. 13.4 - Changing the order of integration Rewrite the...Ch. 13.4 - Changing the order of integration Rewrite the...Ch. 13.4 - Changing the order of integration Rewrite the...Ch. 13.4 - Average value Find the following average values....Ch. 13.4 - Prob. 44ECh. 13.4 - Average value Find the following average values....Ch. 13.4 - Prob. 46ECh. 13.4 - Average value Find the following average values....Ch. 13.4 - Prob. 48ECh. 13.4 - Explain why or why not Determine whether the...Ch. 13.4 - Changing the order of integration Use another...Ch. 13.4 - Prob. 51ECh. 13.4 - Prob. 52ECh. 13.4 - Miscellaneous volumes Use a triple integral to...Ch. 13.4 - Miscellaneous volumes Use a triple integral to...Ch. 13.4 - Prob. 55ECh. 13.4 - Prob. 56ECh. 13.4 - Changing order of integration Write the integral...Ch. 13.4 - All six orders Let D be the solid bounded by y =...Ch. 13.4 - Prob. 59ECh. 13.4 - Dividing the cheese Suppose a wedge of cheese...Ch. 13.4 - General volume formulas Find equations for the...Ch. 13.4 - Prob. 62ECh. 13.4 - General volume formulas Find equations for the...Ch. 13.4 - Prob. 64ECh. 13.4 - Prob. 65ECh. 13.4 - Prob. 66ECh. 13.4 - Hypervolume Find the Volume of the...Ch. 13.4 - Prob. 68ECh. 13.5 - Explain how cylindrical coordinates are used to...Ch. 13.5 - Explain how spherical coordinates are used to...Ch. 13.5 - Describe the set {(r, , z): r = 4z} in cylindrical...Ch. 13.5 - Describe the set {(, , ): = /4} in spherical...Ch. 13.5 - Explain why dz r dr d is the volume of a small box...Ch. 13.5 - Explain why 2 sin d d d is the volume of a small...Ch. 13.5 - Prob. 7ECh. 13.5 - Prob. 8ECh. 13.5 - What coordinate system is suggested if the...Ch. 13.5 - What coordinate system is suggested if the...Ch. 13.5 - Sets in cylindrical coordinates Identify and...Ch. 13.5 - Sets in cylindrical coordinates Identify and...Ch. 13.5 - Sets in cylindrical coordinates Identify and...Ch. 13.5 - Sets in cylindrical coordinates Identify and...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Which weighs more? For 0 r 1, the solid bounded...Ch. 13.5 - Prob. 28ECh. 13.5 - Prob. 29ECh. 13.5 - Volumes in cylindrical coordinates Use cylindrical...Ch. 13.5 - Volumes in cylindrical coordinates Use cylindrical...Ch. 13.5 - Volumes in cylindrical coordinates Use cylindrical...Ch. 13.5 - Volumes in cylindrical coordinates Use cylindrical...Ch. 13.5 - Volumes in cylindrical coordinates Use cylindrical...Ch. 13.5 - Prob. 35ECh. 13.5 - Sets in spherical coordinates Identify and sketch...Ch. 13.5 - Sets in spherical coordinates Identify and sketch...Ch. 13.5 - Sets in spherical coordinates Identify and sketch...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Explain why or why not Determine whether the...Ch. 13.5 - Spherical to rectangular Convert the equation 2 =...Ch. 13.5 - Spherical to rectangular Convert the equation 2 =...Ch. 13.5 - Prob. 56ECh. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Changing order of integration If possible, write...Ch. 13.5 - Changing order of integration If possible, write...Ch. 13.5 - Prob. 62ECh. 13.5 - Prob. 63ECh. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Prob. 72ECh. 13.5 - Density distribution A right circular cylinder...Ch. 13.5 - Charge distribution A spherical cloud of electric...Ch. 13.5 - Gravitational field due to spherical shell A point...Ch. 13.5 - Water in a gas tank Before a gasoline-powered...Ch. 13.5 - General volume formulas Use integration to find...Ch. 13.5 - Prob. 78ECh. 13.5 - General volume formulas Use integration to find...Ch. 13.5 - Prob. 80ECh. 13.5 - Intersecting spheres One sphere is centered at the...Ch. 13.6 - Explain how to find the balance point for two...Ch. 13.6 - If a thin 1-m cylindrical rod has a density of =...Ch. 13.6 - Explain how to find the center of mass of a thin...Ch. 13.6 - In the integral for the moment Mx of a thin plate,...Ch. 13.6 - Explain how to find the center of mass of a...Ch. 13.6 - In the integral for the moment Mxz with respect to...Ch. 13.6 - Individual masses on a line Sketch the following...Ch. 13.6 - Individual masses on a line Sketch the following...Ch. 13.6 - One-dimensional objects Find the mass and center...Ch. 13.6 - One-dimensional objects Find the mass and center...Ch. 13.6 - One-dimensional objects Find the mass and center...Ch. 13.6 - One-dimensional objects Find the mass and center...Ch. 13.6 - One-dimensional objects Find the mass and center...Ch. 13.6 - Prob. 14ECh. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Explain why or why not Determine whether the...Ch. 13.6 - Limiting center of mass A thin rod of length L has...Ch. 13.6 - Limiting center of mass A thin rod of length L has...Ch. 13.6 - Prob. 42ECh. 13.6 - Two-dimensional plates Find the mass and center of...Ch. 13.6 - Two-dimensional plates Find the mass and center of...Ch. 13.6 - Centroids Use polar coordinates to find the...Ch. 13.6 - Prob. 46ECh. 13.6 - Centroids Use polar coordinates to find the...Ch. 13.6 - Centroids Use polar coordinates to find the...Ch. 13.6 - Prob. 49ECh. 13.6 - Prob. 50ECh. 13.6 - Prob. 51ECh. 13.6 - Prob. 52ECh. 13.6 - Prob. 53ECh. 13.6 - Prob. 54ECh. 13.6 - Centers of mass for general objects Consider the...Ch. 13.6 - Centers of mass for general objects Consider the...Ch. 13.6 - Prob. 57ECh. 13.6 - Centers of mass for general objects Consider the...Ch. 13.6 - Centers of mass for general objects Consider the...Ch. 13.6 - Geographic vs. population center Geographers...Ch. 13.6 - Center of mass on the edge Consider the thin...Ch. 13.6 - Center of mass on the edge Consider the...Ch. 13.6 - Draining a soda can A cylindrical soda can has a...Ch. 13.6 - Triangle medians A triangular region has a base...Ch. 13.6 - The golden earring A disk of radius r is removed...Ch. 13.7 - Suppose S is the unit square in the first quadrant...Ch. 13.7 - Explain how to compute the Jacobian of the...Ch. 13.7 - Using the transformation T: x = u + v, y = u v,...Ch. 13.7 - Suppose S is the unit cube in the first octant of...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Images of regions Find the image R in the xy-plane...Ch. 13.7 - Images of regions Find the image R in the xy-plane...Ch. 13.7 - Images of regions Find the image R in the xy-plane...Ch. 13.7 - Images of regions Find the image R in the xy-plane...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Solve and compute Jacobians Solve the following...Ch. 13.7 - Solve and compute Jacobians Solve the following...Ch. 13.7 - Solve and compute Jacobians Solve the following...Ch. 13.7 - Solve and compute Jacobians Solve the following...Ch. 13.7 - Double integralstransformation given To evaluate...Ch. 13.7 - Double integralstransformation given To evaluate...Ch. 13.7 - Double integralstransformation given To evaluate...Ch. 13.7 - Double integralstransformation given To evaluate...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Jacobians in three variables Evaluate the...Ch. 13.7 - Prob. 38ECh. 13.7 - Jacobians in three variables Evaluate the...Ch. 13.7 - Jacobians in three variables Evaluate the...Ch. 13.7 - Triple integrals Use a change of variables to...Ch. 13.7 - Triple integrals Use a change of variables to...Ch. 13.7 - Triple integrals Use a change of variables to...Ch. 13.7 - Triple integrals Use a change of variables to...Ch. 13.7 - Explain why or why not Determine whether the...Ch. 13.7 - Prob. 46ECh. 13.7 - Prob. 47ECh. 13.7 - Ellipse problems Let R be the region bounded by...Ch. 13.7 - Ellipse problems Let R be the region bounded by...Ch. 13.7 - Ellipse problems Let R be the region bounded by...Ch. 13.7 - Ellipse problems Let R be the region bounded by...Ch. 13.7 - Ellipse problems Let R be the region bounded by...Ch. 13.7 - Ellipsoid problems Let D be the solid bounded by...Ch. 13.7 - Ellipsoid problems Let D be the solid bounded by...Ch. 13.7 - Ellipsoid problems Let D be the solid bounded by...Ch. 13.7 - Ellipsoid problems Let D be the solid bounded by...Ch. 13.7 - Parabolic coordinates Let T be the transformation...Ch. 13.7 - Shear transformations in 3 The transformation T in...Ch. 13.7 - Linear transformations Consider the linear...Ch. 13.7 - Meaning of the Jacobian The Jacobian is a...Ch. 13.7 - Open and closed boxes Consider the region R...Ch. 13 - Explain why or why not Determine whether the...Ch. 13 - Evaluating integrals Evaluate the following...Ch. 13 - Evaluating integrals Evaluate the following...Ch. 13 - Evaluating integrals Evaluate the following...Ch. 13 - Changing the order of integration Assuming f is...Ch. 13 - Changing the order of integration Assuming f is...Ch. 13 - Changing the order of integration Assuming f is...Ch. 13 - Area of plane regions Use double integrals to...Ch. 13 - Area of plane regions Use double integrals to...Ch. 13 - Area of plane regions Use double integrals to...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Cartesian to polar coordinates Evaluate the...Ch. 13 - Cartesian to polar coordinates Evaluate the...Ch. 13 - Computing areas Sketch the following regions and...Ch. 13 - Computing areas Sketch the following regions and...Ch. 13 - Computing areas Sketch the following regions and...Ch. 13 - Average values 22.Find the average value of...Ch. 13 - Average values 23.Find the average distance from...Ch. 13 - Prob. 24RECh. 13 - Prob. 25RECh. 13 - Changing order of integration Rewrite the...Ch. 13 - Triple integrals Evaluate the following integrals,...Ch. 13 - Triple integrals Evaluate the following integrals,...Ch. 13 - Triple integrals Evaluate the following integrals,...Ch. 13 - Triple integrals Evaluate the following integrals,...Ch. 13 - Triple integrals Evaluate the following integrals,...Ch. 13 - Volumes of solids Find the volume of the following...Ch. 13 - Volumes of solids Find the volume of the following...Ch. 13 - Volumes of solids Find the volume of the following...Ch. 13 - Volumes of solids Find the volume of the following...Ch. 13 - Volumes of solids Find the volume of the following...Ch. 13 - Single to double integral Evaluate...Ch. 13 - Tetrahedron limits Let D be the tetrahedron with...Ch. 13 - A polynomial cube Let D = {(x, y, z): 0 x y2, 0 ...Ch. 13 - Average value 40.Find the average of the square of...Ch. 13 - Average value 41.Find the average x-coordinate of...Ch. 13 - Integrals in cylindrical coordinates Evaluate the...Ch. 13 - Integrals in cylindrical coordinates Evaluate the...Ch. 13 - Volumes in cylindrical coordinates Use integration...Ch. 13 - Volumes in cylindrical coordinates Use integration...Ch. 13 - Integrals in spherical coordinates Evaluate the...Ch. 13 - Integrals in spherical coordinates Evaluate the...Ch. 13 - Volumes in spherical coordinates Use integration...Ch. 13 - Volumes in spherical coordinates Use integration...Ch. 13 - Volumes in spherical coordinates Use integration...Ch. 13 - Center of mass of constant-density plates Find the...Ch. 13 - Center of mass of constant-density plates Find the...Ch. 13 - Center of mass of constant-density plates Find the...Ch. 13 - Center of mass of constant-density plates Find the...Ch. 13 - Center of mass of constant-density solids Find the...Ch. 13 - Center of mass of constant-density solids Find the...Ch. 13 - Prob. 57RECh. 13 - Variable-density solids Find the coordinates of...Ch. 13 - Center of mass for general objects Consider the...Ch. 13 - Prob. 60RECh. 13 - Prob. 61RECh. 13 - Prob. 62RECh. 13 - Volume and weight of a fish tank A spherical fish...Ch. 13 - Prob. 65RECh. 13 - Transforming a square Let S = {(u, v): 0 u 1, 0...Ch. 13 - Prob. 67RECh. 13 - Transforming a square Let S = {(u, v): 0 u 1, 0...Ch. 13 - Prob. 69RECh. 13 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13 - Prob. 71RECh. 13 - Prob. 72RECh. 13 - Double integralstransformation given To evaluate...Ch. 13 - Double integralstransformation given To evaluate...Ch. 13 - Double integralstransformation given To evaluate...Ch. 13 - Double integralstransformation given To evaluate...Ch. 13 - Double integrals Evaluate the following integrals...Ch. 13 - Double integrals Evaluate the following integrals...Ch. 13 - Triple integrals Use a change of variables to...Ch. 13 - Triple integrals Use a change of variables to...
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Text book image
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Text book image
College Algebra
Algebra
ISBN:9781938168383
Author:Jay Abramson
Publisher:OpenStax
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Continuous Probability Distributions - Basic Introduction; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=QxqxdQ_g2uw;License: Standard YouTube License, CC-BY
Probability Density Function (p.d.f.) Finding k (Part 1) | ExamSolutions; Author: ExamSolutions;https://www.youtube.com/watch?v=RsuS2ehsTDM;License: Standard YouTube License, CC-BY
Find the value of k so that the Function is a Probability Density Function; Author: The Math Sorcerer;https://www.youtube.com/watch?v=QqoCZWrVnbA;License: Standard Youtube License