Pearson eText for Mathematics for Elementary Teachers with Activities -- Instant Access (Pearson+)
5th Edition
ISBN: 9780137442812
Author: Sybilla Beckmann
Publisher: PEARSON+
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13.3, Problem 14P
The front (and back) of a greenhouse have the shape and dimensions shown in Figure 13.36 . The greenhouse is 40 ft long, and the angle at the top of the roof is 90°. A fungus has begun to grow in the greenhouse. so a fungicide will need to be sprayed. The fungicide is simply sprayed into the air. To be effective, 1 tablespoon of fungicide is needed for every cubic yard of volume in the greenhouse. How much fungicide should be used? Give your answer in terms of units that are practical. (For example, it would not be practical to have to measure 100 tablespoons, nor would it be practical to have to measure 3.4 quarts. But it would be practical to measure 1 quart and 3 fluid ounces.) Explain
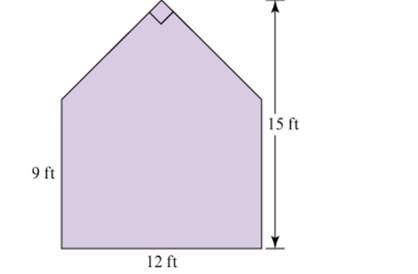
Figure 13.36 A greenhouse
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
x² + 3x - 28
Simplify the expression x² - 7x+12. Show
nswer:
your work.
A savings account is started with an initial deposit of $500. The
account earns 1.5% interest compounded annually.
(a) Write an equation to represent the amount of money in
the account as a function of time in years.
(b)
Find the amount of time it takes for the account balance
to reach $800. Show your work.
(a) Use the fundamental theorem of algebra to determine the number of roots for 2x² +4x+7.
(b) What are the roots of 2x² +4x+7? Show your work.
Chapter 13 Solutions
Pearson eText for Mathematics for Elementary Teachers with Activities -- Instant Access (Pearson+)
Ch. 13.1 - For each of the following solid shapes, find at...Ch. 13.1 - Answer the following questions without using a...Ch. 13.1 - Answer the following questions without using a...Ch. 13.1 - Recall that an n-gon is a polygon with n side For...Ch. 13.1 - This problem goes with Class Activity 13C on the...Ch. 13.1 - Referring to the descriptions of the Platonic...Ch. 13.1 - A cube is a polyhedron that has 3 square faces...Ch. 13.1 - The Platonic solids are convex polyhedra with...Ch. 13.1 - Two gorgeous polyhedra can be created by...Ch. 13.2 - Find all the different nets for a tetrahedron made...
Ch. 13.2 - Make three different nets that could be cut out,...Ch. 13.2 - Describe or show how to make a cylinder without...Ch. 13.2 - If a cardboard box (rectangular prism) with a top,...Ch. 13.2 - Use a ruler and compass to help you make a pattern...Ch. 13.2 - Use a ruler and compass to help you make a pattern...Ch. 13.2 - Use a ruler and compass to help you make a pattern...Ch. 13.2 - Prob. 8PCh. 13.2 - Make a pattern for the “bottom portion” (frustum)...Ch. 13.2 - A company will manufacture a tent that will have a...Ch. 13.2 - Prob. 11PCh. 13.2 - Prob. 12PCh. 13.2 - A popular brand of soup comes in cans that are 258...Ch. 13.2 - The lateral portion of a cone (the part other than...Ch. 13.2 - Make a pattern for a cone such that the lateral...Ch. 13.2 - Make a pattern for a cone such that the lateral...Ch. 13.2 - A cone with a circular base of radius 6 cm is to...Ch. 13.2 - Tim needs a sturdy cardboard box that is 3 ft tall...Ch. 13.2 - Prob. 19PCh. 13.2 - Prob. 20PCh. 13.2 - Prob. 21PCh. 13.2 - Prob. 22PCh. 13.2 - How many different nets an open top cubes an...Ch. 13.2 - Make three different nets that could be cut out,...Ch. 13.3 - Suppose that a student in your class wants to know...Ch. 13.3 - Students are sometimes confused about the...Ch. 13.3 - Young children sometimes think that tall...Ch. 13.3 - Students often confuse the surface area and the...Ch. 13.3 - In your own words, explain why the volume volume =...Ch. 13.3 - Discuss how to use blocks to explain why the...Ch. 13.3 - A cylindrical container has a base that is a...Ch. 13.3 - One liter of water is in a cylindrical container....Ch. 13.3 - Measure how fast water comes out of some faucet of...Ch. 13.3 - Find a gallon container, 3 half-gallon container,...Ch. 13.3 - One gallon is 3.79 L, and 1 cm3 holds 1 mL of...Ch. 13.3 - A cake recipe will make a round cake that is 6 in....Ch. 13.3 - A recipe for gingerbread makes a...Ch. 13.3 - The front (and back) of a greenhouse have the...Ch. 13.3 - Prob. 15PCh. 13.3 - Fifty pounds of wrapping paper are wound onto a...Ch. 13.3 - A conveyor belt dumps 2500 yd3 of gravel to form a...Ch. 13.3 - A construction company wants to know how much sand...Ch. 13.3 - One of the Hawaiian volcanoes is 30,000 ft high...Ch. 13.3 - Prob. 20PCh. 13.3 - Prob. 21PCh. 13.3 - A cone without a base is made from a...Ch. 13.3 - Prob. 23PCh. 13.3 - A cone without a base is made from 34 of a circle...Ch. 13.3 - A cone-shaped cup has a circular opening at the...Ch. 13.3 - Eight identical spherical raindrops join together...Ch. 13.4 - A tank in the shape of a rectangular prism has a...Ch. 13.4 - A container holds 5 liters. Initially, the...Ch. 13.4 - Aflsh tank in the shape of a rectangular prism is...Ch. 13.4 - Suppose that you have a recipe that calls for 200...Ch. 13.4 - Prob. 5P
Additional Math Textbook Solutions
Find more solutions based on key concepts
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
Silvia wants to mix a 40% apple juice drink with pure apple juice to make 2 L of a juice drink that is 80% appl...
Beginning and Intermediate Algebra
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
Teacher Salaries
The following data from several years ago represent salaries (in dollars) from a school distri...
Elementary Statistics: A Step By Step Approach
153. A rain gutter is made from sheets of aluminum that are 20 inches wide. As shown in the figure, the edges ...
College Algebra (7th Edition)
Fill in each blank so that the resulting statement is true.
1. The degree of the polynomial function is _____....
Algebra and Trigonometry (6th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Consider the function f(x)=x³ + 2x² − 3 (a) Graph the function. (b) What are the x- and y-intercepts of the graph?arrow_forwardTriangle ΔABC has side lengths of a = 15, b equals 15 times square root of 3 and c = 30 inches. Part A: Determine the measure of angle m∠B. Part B: Show how to use the unit circle to find tan B. Part C: Calculate the area of ΔABC.arrow_forwardPart A: Given sinθ = square root of 3/2, determine three possible angles θ on the domain [0,∞).Part B: Given θ = 675°, convert the value of θ to radians and find sec θ.arrow_forward
- 7. Rank and Nullity • Prove the Rank-Nullity Theorem: dim(ker(T)) + dim(im(T)) = dim(V) for a linear transformation T: VW. • Compute the rank and nullity of the matrix: [1 2 37 C = 45 6 7 8 9arrow_forward5. Inner Product Spaces • • Prove that the space C[a, b] of continuous functions over [a, b] with the inner product (f,g) = f f (x)g(x)dx is an inner product space. Use the Gram-Schmidt process to orthogonalize the vectors (1, 1, 0), (1, 0, 1), and (0, 1, 1).arrow_forward19. Block Matrices • Prove that the determinant of a block matrix: A B 0 D . is det(A) · det (D), where A and D are square matrices. • Show how block matrices are used in solving large-scale linear systems.arrow_forward
- 6. Norms and Metrics • Show that the function || || norm on Rn. = √xT Ax, where A is a positive definite matrix, defines a . Prove that the matrix norm induced by the vector L²-norm satisfies ||A||2 ✓ max (ATA), where Amax is the largest eigenvalue.arrow_forward2. Linear Transformations • • Let T: R3 R³ be a linear transformation such that T(x, y, z) = (x + y, y + z, z + → x). Find the matrix representation of T with respect to the standard basis. Prove that a linear transformation T : VV is invertible if and only if it is bijective.arrow_forward11. Positive Definiteness Prove that a matrix A is positive definite if and only if all its eigenvalues are positive.arrow_forward
- 21. Change of Basis Prove that the matrix representation of a linear transformation T : V → V depends on the choice of basis in V. If P is a change of basis matrix, show that the transformation matrix in the new basis is P-¹AP.arrow_forward14. Projection Matrices Show that if P is a projection matrix, then P² = P. Find the projection matrix onto the subspace spanned by the vector (1,2,2)T.arrow_forward4. Diagonalization Prove that a square matrix A is diagonalizable if and only if A has n linearly independent eigenvectors. • Determine whether the following matrix is diagonalizable: [54 2 B = 01 -1 3arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
ALGEBRAIC EXPRESSIONS & EQUATIONS | GRADE 6; Author: SheenaDoria;https://www.youtube.com/watch?v=fUOdon3y1hU;License: Standard YouTube License, CC-BY
Algebraic Expression And Manipulation For O Level; Author: Maths Solution;https://www.youtube.com/watch?v=MhTyodgnzNM;License: Standard YouTube License, CC-BY
Algebra for Beginners | Basics of Algebra; Author: Geek's Lesson;https://www.youtube.com/watch?v=PVoTRu3p6ug;License: Standard YouTube License, CC-BY
Introduction to Algebra | Algebra for Beginners | Math | LetsTute; Author: Let'stute;https://www.youtube.com/watch?v=VqfeXMinM0U;License: Standard YouTube License, CC-BY