
Student Solutions Manual, Single Variable for Calculus: Early Transcendentals
2nd Edition
ISBN: 9780321954329
Author: William L. Briggs, Lyle Cochran, Bernard Gillett
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 13.2, Problem 69E
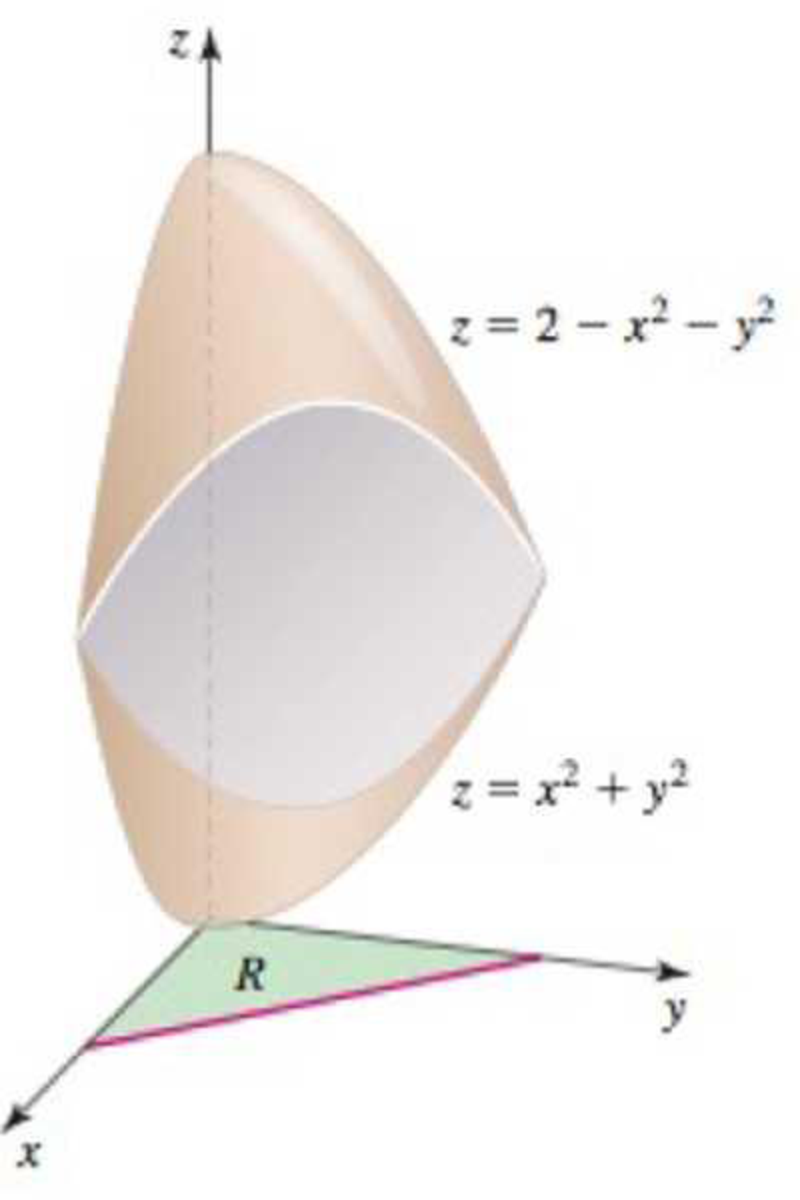
Regions between surfaces Find the volume of the following solid regions.
69. The solid above the region R = {(x, y): 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 – x} bounded by the paraboloids z = x2 + y2 and z = 2 – x2 – y2, and the coordinate planes in the first octant
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Evaluate the definite integral using the given integration limits and the limits obtained by trigonometric substitution.
14
x²
dx
249
(a) the given integration limits
(b) the limits obtained by trigonometric substitution
Assignment #1
Q1: Test the following series for convergence. Specify the test you use:
1
n+5
(-1)n
a) Σn=o
√n²+1
b) Σn=1 n√n+3
c) Σn=1 (2n+1)3
3n
1
d) Σn=1 3n-1
e) Σn=1
4+4n
answer problem 1a, 1b, 1c, 1d, and 1e and show work/ explain how you got the answer
Chapter 13 Solutions
Student Solutions Manual, Single Variable for Calculus: Early Transcendentals
Ch. 13.1 - 1. Write an iterated integral that gives the...Ch. 13.1 - Write an iterated integral that gives the volume...Ch. 13.1 - Write two iterated integrals that equal Rf(x,y)dA,...Ch. 13.1 - Consider the integral 1311(2y2+xy)dydx. State the...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...
Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Prob. 12ECh. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Iterated integrals Evaluate the following iterated...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Prob. 20ECh. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Double integrals Evaluate each double integral...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Choose a convenient order When convened to an...Ch. 13.1 - Average value Compute the average value of the...Ch. 13.1 - Average value Compute the average value of the...Ch. 13.1 - Average value Compute the average value of the...Ch. 13.1 - Average value 35.Find the average squared distance...Ch. 13.1 - Average value 35.Find the average squared distance...Ch. 13.1 - Explain why or why not Determine whether the...Ch. 13.1 - Symmetry Evaluate the following integrals using...Ch. 13.1 - Computing populations The population densities in...Ch. 13.1 - Prob. 40ECh. 13.1 - Pictures of solids Draw the solid whose volume is...Ch. 13.1 - Prob. 42ECh. 13.1 - More integration practice Evaluate the following...Ch. 13.1 - More integration practice Evaluate the following...Ch. 13.1 - More integration practice Evaluate the following...Ch. 13.1 - More integration practice Evaluate the following...Ch. 13.1 - Volumes of solids Find the volume of the following...Ch. 13.1 - Prob. 48ECh. 13.1 - Volumes of solids Find the volume of the following...Ch. 13.1 - Prob. 50ECh. 13.1 - Solving for a parameter Let R={x,y}:{0x,0ya}. For...Ch. 13.1 - Prob. 52ECh. 13.1 - Zero average value Find the value of a 0 such...Ch. 13.1 - Prob. 54ECh. 13.1 - Density and mass Suppose a thin rectangular plate,...Ch. 13.1 - Approximating volume Propose a method based on...Ch. 13.1 - Cylinders Let S be the solid in 3between the...Ch. 13.1 - Product of integrals Suppose f(x, y) = g(x)h(y),...Ch. 13.1 - Prob. 59ECh. 13.1 - Prob. 60ECh. 13.1 - A generalization Let R be as in Exercise 60, let F...Ch. 13.2 - Describe and sketch a region that is bounded above...Ch. 13.2 - Describe and a sketch a region that is bounded on...Ch. 13.2 - Which order of integration is preferable to...Ch. 13.2 - Which order of integration would you use to find...Ch. 13.2 - Change the order of integration in the integral...Ch. 13.2 - Sketch the region of integration for 22x24exydydxCh. 13.2 - Regions of integration Consider the regions R...Ch. 13.2 - Regions of integration Consider the regions R...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Prob. 20ECh. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Prob. 22ECh. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Regions of integration Write an iterated integral...Ch. 13.2 - Regions of integration Write an iterated integral...Ch. 13.2 - Prob. 33ECh. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Regions of integration Sketch each region and...Ch. 13.2 - Prob. 37ECh. 13.2 - Prob. 38ECh. 13.2 - Prob. 39ECh. 13.2 - Prob. 40ECh. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Prob. 42ECh. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Evaluating integrals Evaluate the following...Ch. 13.2 - Prob. 52ECh. 13.2 - Volumes Use double integrals to calculate the...Ch. 13.2 - Volumes Use double integrals to calculate the...Ch. 13.2 - Volumes Use double integrals to calculate the...Ch. 13.2 - Prob. 56ECh. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Changing order of integration Reverse the order of...Ch. 13.2 - Prob. 63ECh. 13.2 - Changing order of integration The following...Ch. 13.2 - Prob. 65ECh. 13.2 - Changing order of integration The following...Ch. 13.2 - Prob. 67ECh. 13.2 - Changing order of integration The following...Ch. 13.2 - Regions between surfaces Find the volume of the...Ch. 13.2 - Prob. 70ECh. 13.2 - Regions between surfaces Find the volume of the...Ch. 13.2 - Regions between surfaces Find the volume of the...Ch. 13.2 - Regions between surfaces Find the volume of the...Ch. 13.2 - Regions between surfaces Find the volume of the...Ch. 13.2 - Prob. 75ECh. 13.2 - Prob. 76ECh. 13.2 - Prob. 77ECh. 13.2 - Prob. 78ECh. 13.2 - Prob. 79ECh. 13.2 - Prob. 80ECh. 13.2 - Explain why or why not Determine whether the...Ch. 13.2 - Prob. 82ECh. 13.2 - Prob. 83ECh. 13.2 - Prob. 84ECh. 13.2 - Prob. 85ECh. 13.2 - Prob. 86ECh. 13.2 - Two integrals to one Draw the regions of...Ch. 13.2 - Square region Consider the region R = {(x, y): |x|...Ch. 13.2 - Prob. 89ECh. 13.2 - Prob. 90ECh. 13.2 - Area integrals Consider the following regions R....Ch. 13.2 - Area integrals Consider the following regions R....Ch. 13.2 - Prob. 93ECh. 13.2 - Prob. 94ECh. 13.2 - Prob. 95ECh. 13.2 - Prob. 96ECh. 13.2 - Volumes Compute the volume of the following...Ch. 13.2 - Prob. 99ECh. 13.2 - Prob. 100ECh. 13.2 - Prob. 101ECh. 13.2 - Prob. 102ECh. 13.2 - Prob. 103ECh. 13.3 - Draw the region {(r, ): 1 r 2, 0 /2}. Why is...Ch. 13.3 - Write the double integral Rf(x,y)dAas an iterated...Ch. 13.3 - Sketch the region of integration for the integral...Ch. 13.3 - Prob. 4ECh. 13.3 - How do you find the area of a region R = {(r, ):...Ch. 13.3 - How do you find the average value of a function...Ch. 13.3 - Polar rectangles Sketch the following polar...Ch. 13.3 - Polar rectangles Sketch the following polar...Ch. 13.3 - Polar rectangles Sketch the following polar...Ch. 13.3 - Polar rectangles Sketch the following polar...Ch. 13.3 - Solids bounded by paraboloids Find the volume of...Ch. 13.3 - Solids bounded by paraboloids Find the volume of...Ch. 13.3 - Solids bounded by paraboloids Find the volume of...Ch. 13.3 - Solids bounded by paraboloids Find the volume of...Ch. 13.3 - Solids bounded by hyperboloids Find the volume of...Ch. 13.3 - Solids bounded by hyperboloids Find the volume of...Ch. 13.3 - Solids bounded by hyperboloids Find the volume of...Ch. 13.3 - Solids bounded by hyperboloids Find the volume of...Ch. 13.3 - Volume between surfaces Find the volume of the...Ch. 13.3 - Volume between surfaces Find the volume of the...Ch. 13.3 - Volume between surfaces Find the volume of the...Ch. 13.3 - Prob. 22ECh. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Cartesian to polar coordinates Sketch the given...Ch. 13.3 - Island problems The surface of an island is...Ch. 13.3 - Island problems The surface of an island is...Ch. 13.3 - Island problems The surface of an island is...Ch. 13.3 - Prob. 32ECh. 13.3 - Describing general regions Sketch the following...Ch. 13.3 - Prob. 34ECh. 13.3 - Describing general regions Sketch the following...Ch. 13.3 - Describing general regions Sketch the following...Ch. 13.3 - Describing general regions Sketch the following...Ch. 13.3 - Describing general regions Sketch the following...Ch. 13.3 - Computing areas Sketch each region and use a...Ch. 13.3 - Computing areas Sketch each region and use a...Ch. 13.3 - Computing areas Sketch each region and use a...Ch. 13.3 - Computing areas Sketch each region and use a...Ch. 13.3 - Computing areas Sketch each region and use a...Ch. 13.3 - Prob. 44ECh. 13.3 - Average values Find the following average values....Ch. 13.3 - Prob. 46ECh. 13.3 - Prob. 47ECh. 13.3 - Average values Find the following average values....Ch. 13.3 - Explain why or why not Determine whether the...Ch. 13.3 - Prob. 50ECh. 13.3 - Miscellaneous integrals Evaluate the following...Ch. 13.3 - Miscellaneous integrals Evaluate the following...Ch. 13.3 - Miscellaneous integrals Evaluate the following...Ch. 13.3 - Prob. 54ECh. 13.3 - Prob. 55ECh. 13.3 - Miscellaneous integrals Evaluate the following...Ch. 13.3 - Miscellaneous integrals Evaluate the following...Ch. 13.3 - Areas of circles Use integration to show that the...Ch. 13.3 - Filling bowls with water Which bowl holds more...Ch. 13.3 - Prob. 60ECh. 13.3 - Volume of a hyperbolic paraboloid Consider the...Ch. 13.3 - Prob. 62ECh. 13.3 - Improper integrals Improper integrals arise in...Ch. 13.3 - Improper integrals Improper integrals arise in...Ch. 13.3 - Improper integrals Improper integrals arise in...Ch. 13.3 - Improper integrals Improper integrals arise in...Ch. 13.3 - Prob. 67ECh. 13.3 - Mass from density data The following table gives...Ch. 13.3 - A mass calculation Suppose the density of a thin...Ch. 13.3 - Prob. 70ECh. 13.3 - Prob. 71ECh. 13.3 - Existence of integrals For what values of p does...Ch. 13.3 - Integrals in strips Consider the integral...Ch. 13.3 - Prob. 74ECh. 13.4 - Sketch the region D = {(x, y, z): x2 + y2 4, 0 z...Ch. 13.4 - Write an iterated integral for Df(x,y,z)dV, where...Ch. 13.4 - Write an iterated integral for Df(x,y,z)dV, where...Ch. 13.4 - Sketch the region of integration for the integral...Ch. 13.4 - Write the integral in Exercise 4 in the order dy...Ch. 13.4 - Write an integral for the average value of f(x, y,...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Integrals over boxes Evaluate the following...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Volumes of solids. Find the volume of the...Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Triple integrals Evaluate the following integrals....Ch. 13.4 - Prob. 34ECh. 13.4 - Finding an appropriate order of integration Find...Ch. 13.4 - Finding an appropriate order of integration Find...Ch. 13.4 - Finding an appropriate order of integration Find...Ch. 13.4 - Finding an appropriate order of integration Find...Ch. 13.4 - Changing the order of integration Rewrite the...Ch. 13.4 - Changing the order of integration Rewrite the...Ch. 13.4 - Changing the order of integration Rewrite the...Ch. 13.4 - Changing the order of integration Rewrite the...Ch. 13.4 - Average value Find the following average values....Ch. 13.4 - Prob. 44ECh. 13.4 - Average value Find the following average values....Ch. 13.4 - Prob. 46ECh. 13.4 - Average value Find the following average values....Ch. 13.4 - Prob. 48ECh. 13.4 - Explain why or why not Determine whether the...Ch. 13.4 - Changing the order of integration Use another...Ch. 13.4 - Prob. 51ECh. 13.4 - Prob. 52ECh. 13.4 - Miscellaneous volumes Use a triple integral to...Ch. 13.4 - Miscellaneous volumes Use a triple integral to...Ch. 13.4 - Prob. 55ECh. 13.4 - Prob. 56ECh. 13.4 - Changing order of integration Write the integral...Ch. 13.4 - All six orders Let D be the solid bounded by y =...Ch. 13.4 - Prob. 59ECh. 13.4 - Dividing the cheese Suppose a wedge of cheese...Ch. 13.4 - General volume formulas Find equations for the...Ch. 13.4 - Prob. 62ECh. 13.4 - General volume formulas Find equations for the...Ch. 13.4 - Prob. 64ECh. 13.4 - Prob. 65ECh. 13.4 - Prob. 66ECh. 13.4 - Hypervolume Find the Volume of the...Ch. 13.4 - Prob. 68ECh. 13.5 - Explain how cylindrical coordinates are used to...Ch. 13.5 - Explain how spherical coordinates are used to...Ch. 13.5 - Describe the set {(r, , z): r = 4z} in cylindrical...Ch. 13.5 - Describe the set {(, , ): = /4} in spherical...Ch. 13.5 - Explain why dz r dr d is the volume of a small box...Ch. 13.5 - Explain why 2 sin d d d is the volume of a small...Ch. 13.5 - Prob. 7ECh. 13.5 - Prob. 8ECh. 13.5 - What coordinate system is suggested if the...Ch. 13.5 - What coordinate system is suggested if the...Ch. 13.5 - Sets in cylindrical coordinates Identify and...Ch. 13.5 - Sets in cylindrical coordinates Identify and...Ch. 13.5 - Sets in cylindrical coordinates Identify and...Ch. 13.5 - Sets in cylindrical coordinates Identify and...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Integrals in cylindrical coordinates Evaluate the...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Which weighs more? For 0 r 1, the solid bounded...Ch. 13.5 - Prob. 28ECh. 13.5 - Prob. 29ECh. 13.5 - Volumes in cylindrical coordinates Use cylindrical...Ch. 13.5 - Volumes in cylindrical coordinates Use cylindrical...Ch. 13.5 - Volumes in cylindrical coordinates Use cylindrical...Ch. 13.5 - Volumes in cylindrical coordinates Use cylindrical...Ch. 13.5 - Volumes in cylindrical coordinates Use cylindrical...Ch. 13.5 - Prob. 35ECh. 13.5 - Sets in spherical coordinates Identify and sketch...Ch. 13.5 - Sets in spherical coordinates Identify and sketch...Ch. 13.5 - Sets in spherical coordinates Identify and sketch...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Integrals in spherical coordinates Evaluate the...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Volumes in spherical coordinates Use spherical...Ch. 13.5 - Explain why or why not Determine whether the...Ch. 13.5 - Spherical to rectangular Convert the equation 2 =...Ch. 13.5 - Spherical to rectangular Convert the equation 2 =...Ch. 13.5 - Prob. 56ECh. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Mass from density Find the mass of the following...Ch. 13.5 - Changing order of integration If possible, write...Ch. 13.5 - Changing order of integration If possible, write...Ch. 13.5 - Prob. 62ECh. 13.5 - Prob. 63ECh. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Miscellaneous volumes Choose the best coordinate...Ch. 13.5 - Prob. 72ECh. 13.5 - Density distribution A right circular cylinder...Ch. 13.5 - Charge distribution A spherical cloud of electric...Ch. 13.5 - Gravitational field due to spherical shell A point...Ch. 13.5 - Water in a gas tank Before a gasoline-powered...Ch. 13.5 - General volume formulas Use integration to find...Ch. 13.5 - Prob. 78ECh. 13.5 - General volume formulas Use integration to find...Ch. 13.5 - Prob. 80ECh. 13.5 - Intersecting spheres One sphere is centered at the...Ch. 13.6 - Explain how to find the balance point for two...Ch. 13.6 - If a thin 1-m cylindrical rod has a density of =...Ch. 13.6 - Explain how to find the center of mass of a thin...Ch. 13.6 - In the integral for the moment Mx of a thin plate,...Ch. 13.6 - Explain how to find the center of mass of a...Ch. 13.6 - In the integral for the moment Mxz with respect to...Ch. 13.6 - Individual masses on a line Sketch the following...Ch. 13.6 - Individual masses on a line Sketch the following...Ch. 13.6 - One-dimensional objects Find the mass and center...Ch. 13.6 - One-dimensional objects Find the mass and center...Ch. 13.6 - One-dimensional objects Find the mass and center...Ch. 13.6 - One-dimensional objects Find the mass and center...Ch. 13.6 - One-dimensional objects Find the mass and center...Ch. 13.6 - Prob. 14ECh. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Centroid calculations Find the mass and centroid...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Variable-density plates Find the center of mass of...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Center of mass of constant-density solids Find the...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Variable-density solids Find the coordinates of...Ch. 13.6 - Explain why or why not Determine whether the...Ch. 13.6 - Limiting center of mass A thin rod of length L has...Ch. 13.6 - Limiting center of mass A thin rod of length L has...Ch. 13.6 - Prob. 42ECh. 13.6 - Two-dimensional plates Find the mass and center of...Ch. 13.6 - Two-dimensional plates Find the mass and center of...Ch. 13.6 - Centroids Use polar coordinates to find the...Ch. 13.6 - Prob. 46ECh. 13.6 - Centroids Use polar coordinates to find the...Ch. 13.6 - Centroids Use polar coordinates to find the...Ch. 13.6 - Prob. 49ECh. 13.6 - Prob. 50ECh. 13.6 - Prob. 51ECh. 13.6 - Prob. 52ECh. 13.6 - Prob. 53ECh. 13.6 - Prob. 54ECh. 13.6 - Centers of mass for general objects Consider the...Ch. 13.6 - Centers of mass for general objects Consider the...Ch. 13.6 - Prob. 57ECh. 13.6 - Centers of mass for general objects Consider the...Ch. 13.6 - Centers of mass for general objects Consider the...Ch. 13.6 - Geographic vs. population center Geographers...Ch. 13.6 - Center of mass on the edge Consider the thin...Ch. 13.6 - Center of mass on the edge Consider the...Ch. 13.6 - Draining a soda can A cylindrical soda can has a...Ch. 13.6 - Triangle medians A triangular region has a base...Ch. 13.6 - The golden earring A disk of radius r is removed...Ch. 13.7 - Suppose S is the unit square in the first quadrant...Ch. 13.7 - Explain how to compute the Jacobian of the...Ch. 13.7 - Using the transformation T: x = u + v, y = u v,...Ch. 13.7 - Suppose S is the unit cube in the first octant of...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Transforming a square Let S = {(u, v): 0 u l, 0 ...Ch. 13.7 - Images of regions Find the image R in the xy-plane...Ch. 13.7 - Images of regions Find the image R in the xy-plane...Ch. 13.7 - Images of regions Find the image R in the xy-plane...Ch. 13.7 - Images of regions Find the image R in the xy-plane...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13.7 - Solve and compute Jacobians Solve the following...Ch. 13.7 - Solve and compute Jacobians Solve the following...Ch. 13.7 - Solve and compute Jacobians Solve the following...Ch. 13.7 - Solve and compute Jacobians Solve the following...Ch. 13.7 - Double integralstransformation given To evaluate...Ch. 13.7 - Double integralstransformation given To evaluate...Ch. 13.7 - Double integralstransformation given To evaluate...Ch. 13.7 - Double integralstransformation given To evaluate...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Double integralsyour choice of transformation...Ch. 13.7 - Jacobians in three variables Evaluate the...Ch. 13.7 - Prob. 38ECh. 13.7 - Jacobians in three variables Evaluate the...Ch. 13.7 - Jacobians in three variables Evaluate the...Ch. 13.7 - Triple integrals Use a change of variables to...Ch. 13.7 - Triple integrals Use a change of variables to...Ch. 13.7 - Triple integrals Use a change of variables to...Ch. 13.7 - Triple integrals Use a change of variables to...Ch. 13.7 - Explain why or why not Determine whether the...Ch. 13.7 - Prob. 46ECh. 13.7 - Prob. 47ECh. 13.7 - Ellipse problems Let R be the region bounded by...Ch. 13.7 - Ellipse problems Let R be the region bounded by...Ch. 13.7 - Ellipse problems Let R be the region bounded by...Ch. 13.7 - Ellipse problems Let R be the region bounded by...Ch. 13.7 - Ellipse problems Let R be the region bounded by...Ch. 13.7 - Ellipsoid problems Let D be the solid bounded by...Ch. 13.7 - Ellipsoid problems Let D be the solid bounded by...Ch. 13.7 - Ellipsoid problems Let D be the solid bounded by...Ch. 13.7 - Ellipsoid problems Let D be the solid bounded by...Ch. 13.7 - Parabolic coordinates Let T be the transformation...Ch. 13.7 - Shear transformations in 3 The transformation T in...Ch. 13.7 - Linear transformations Consider the linear...Ch. 13.7 - Meaning of the Jacobian The Jacobian is a...Ch. 13.7 - Open and closed boxes Consider the region R...Ch. 13 - Explain why or why not Determine whether the...Ch. 13 - Evaluating integrals Evaluate the following...Ch. 13 - Evaluating integrals Evaluate the following...Ch. 13 - Evaluating integrals Evaluate the following...Ch. 13 - Changing the order of integration Assuming f is...Ch. 13 - Changing the order of integration Assuming f is...Ch. 13 - Changing the order of integration Assuming f is...Ch. 13 - Area of plane regions Use double integrals to...Ch. 13 - Area of plane regions Use double integrals to...Ch. 13 - Area of plane regions Use double integrals to...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Miscellaneous double integrals Choose a convenient...Ch. 13 - Cartesian to polar coordinates Evaluate the...Ch. 13 - Cartesian to polar coordinates Evaluate the...Ch. 13 - Computing areas Sketch the following regions and...Ch. 13 - Computing areas Sketch the following regions and...Ch. 13 - Computing areas Sketch the following regions and...Ch. 13 - Average values 22.Find the average value of...Ch. 13 - Average values 23.Find the average distance from...Ch. 13 - Prob. 24RECh. 13 - Prob. 25RECh. 13 - Changing order of integration Rewrite the...Ch. 13 - Triple integrals Evaluate the following integrals,...Ch. 13 - Triple integrals Evaluate the following integrals,...Ch. 13 - Triple integrals Evaluate the following integrals,...Ch. 13 - Triple integrals Evaluate the following integrals,...Ch. 13 - Triple integrals Evaluate the following integrals,...Ch. 13 - Volumes of solids Find the volume of the following...Ch. 13 - Volumes of solids Find the volume of the following...Ch. 13 - Volumes of solids Find the volume of the following...Ch. 13 - Volumes of solids Find the volume of the following...Ch. 13 - Volumes of solids Find the volume of the following...Ch. 13 - Single to double integral Evaluate...Ch. 13 - Tetrahedron limits Let D be the tetrahedron with...Ch. 13 - A polynomial cube Let D = {(x, y, z): 0 x y2, 0 ...Ch. 13 - Average value 40.Find the average of the square of...Ch. 13 - Average value 41.Find the average x-coordinate of...Ch. 13 - Integrals in cylindrical coordinates Evaluate the...Ch. 13 - Integrals in cylindrical coordinates Evaluate the...Ch. 13 - Volumes in cylindrical coordinates Use integration...Ch. 13 - Volumes in cylindrical coordinates Use integration...Ch. 13 - Integrals in spherical coordinates Evaluate the...Ch. 13 - Integrals in spherical coordinates Evaluate the...Ch. 13 - Volumes in spherical coordinates Use integration...Ch. 13 - Volumes in spherical coordinates Use integration...Ch. 13 - Volumes in spherical coordinates Use integration...Ch. 13 - Center of mass of constant-density plates Find the...Ch. 13 - Center of mass of constant-density plates Find the...Ch. 13 - Center of mass of constant-density plates Find the...Ch. 13 - Center of mass of constant-density plates Find the...Ch. 13 - Center of mass of constant-density solids Find the...Ch. 13 - Center of mass of constant-density solids Find the...Ch. 13 - Prob. 57RECh. 13 - Variable-density solids Find the coordinates of...Ch. 13 - Center of mass for general objects Consider the...Ch. 13 - Prob. 60RECh. 13 - Prob. 61RECh. 13 - Prob. 62RECh. 13 - Volume and weight of a fish tank A spherical fish...Ch. 13 - Prob. 65RECh. 13 - Transforming a square Let S = {(u, v): 0 u 1, 0...Ch. 13 - Prob. 67RECh. 13 - Transforming a square Let S = {(u, v): 0 u 1, 0...Ch. 13 - Prob. 69RECh. 13 - Computing Jacobians Compute the Jacobian J(u, v)...Ch. 13 - Prob. 71RECh. 13 - Prob. 72RECh. 13 - Double integralstransformation given To evaluate...Ch. 13 - Double integralstransformation given To evaluate...Ch. 13 - Double integralstransformation given To evaluate...Ch. 13 - Double integralstransformation given To evaluate...Ch. 13 - Double integrals Evaluate the following integrals...Ch. 13 - Double integrals Evaluate the following integrals...Ch. 13 - Triple integrals Use a change of variables to...Ch. 13 - Triple integrals Use a change of variables to...
Additional Math Textbook Solutions
Find more solutions based on key concepts
If you multiply an odd number by 2 and add 1, is your answer even or odd?
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Identifying a Test In Exercises 21–24, determine whether the hypothesis test is left-tailed, right-tailed, or t...
Elementary Statistics: Picturing the World (7th Edition)
The four flaws in the given survey.
Elementary Statistics
Alternating Series Test Determine whether the following series converge. 15. k=1(1)k+1k3
Calculus: Early Transcendentals (2nd Edition)
1. combination of numbers, variables, and operation symbols is called an algebraic______.
Algebra and Trigonometry (6th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Provethat a) prove that for any irrational numbers there exists? asequence of rational numbers Xn converg to S. b) let S: RR be a sunctions-t. f(x)=(x-1) arc tan (x), xe Q 3(x-1) 1+x² x&Q Show that lim f(x)= 0 14x C) For any set A define the set -A=yarrow_forwardQ2: Find the interval and radius of convergence for the following series: Σ n=1 (-1)η-1 xn narrow_forward8. Evaluate arctan x dx a) xartanx 2 2 In(1 + x²) + C b) xartanx + 1½-3ln(1 + x²) + C c) xartanx + In(1 + x²) + C d) (arctanx)² + C 2 9) Evaluate Inx³ dx 3 a) +C b) ln x² + C c)¾½ (lnx)² d) 3x(lnx − 1) + C - x 10) Determine which integral is obtained when the substitution x = So¹² √1 - x²dx sine is made in the integral πT π π a) √ sin cos e de b) √ cos² de c) c Ꮎ Ꮎ cos² 0 de c) cos e de d) for cos² e de πT 11. Evaluate tan³xdx 1 a) b) c) [1 - In 2] 2 2 c) [1 − In2] d)½½[1+ In 2]arrow_forward12. Evaluate ſ √9-x2 -dx. x2 a) C 9-x2 √9-x2 - x2 b) C - x x arcsin ½-½ c) C + √9 - x² + arcsin x d) C + √9-x2 x2 13. Find the indefinite integral S cos³30 √sin 30 dᎾ . 2√√sin 30 (5+sin²30) √sin 30 (3+sin²30) a) C+ √sin 30(5-sin²30) b) C + c) C + 5 5 5 10 d) C + 2√√sin 30 (3-sin²30) 2√√sin 30 (5-sin²30) e) C + 5 15 14. Find the indefinite integral ( sin³ 4xcos 44xdx. a) C+ (7-5cos24x)cos54x b) C (7-5cos24x)cos54x (7-5cos24x)cos54x - 140 c) C - 120 140 d) C+ (7-5cos24x)cos54x e) C (7-5cos24x)cos54x 4 4 15. Find the indefinite integral S 2x2 dx. ex - a) C+ (x²+2x+2)ex b) C (x² + 2x + 2)e-* d) C2(x²+2x+2)e¯* e) C + 2(x² + 2x + 2)e¯* - c) C2x(x²+2x+2)e¯*arrow_forward4. Which substitution would you use to simplify the following integrand? S a) x = sin b) x = 2 tan 0 c) x = 2 sec 3√√3 3 x3 5. After making the substitution x = = tan 0, the definite integral 2 2 3 a) ៖ ស្លឺ sin s π - dᎾ 16 0 cos20 b) 2/4 10 cos 20 π sin30 6 - dᎾ c) Π 1 cos³0 3 · de 16 0 sin20 1 x²√x²+4 3 (4x²+9)2 π d) cos²8 16 0 sin³0 dx d) x = tan 0 dx simplifies to: de 6. In order to evaluate (tan 5xsec7xdx, which would be the most appropriate strategy? a) Separate a sec²x factor b) Separate a tan²x factor c) Separate a tan xsecx factor 7. Evaluate 3x x+4 - dx 1 a) 3x+41nx + 4 + C b) 31n|x + 4 + C c) 3 ln x + 4+ C d) 3x - 12 In|x + 4| + C x+4arrow_forward1. Abel's Theorem. The goal in this problem is to prove Abel's theorem by following a series of steps (each step must be justified). Theorem 0.1 (Abel's Theorem). If y1 and y2 are solutions of the differential equation y" + p(t) y′ + q(t) y = 0, where p and q are continuous on an open interval, then the Wronskian is given by W (¥1, v2)(t) = c exp(− [p(t) dt), where C is a constant that does not depend on t. Moreover, either W (y1, y2)(t) = 0 for every t in I or W (y1, y2)(t) = 0 for every t in I. 1. (a) From the two equations (which follow from the hypotheses), show that y" + p(t) y₁ + q(t) y₁ = 0 and y½ + p(t) y2 + q(t) y2 = 0, 2. (b) Observe that Hence, conclude that (YY2 - Y1 y2) + P(t) (y₁ Y2 - Y1 Y2) = 0. W'(y1, y2)(t) = yY2 - Y1 y2- W' + p(t) W = 0. 3. (c) Use the result from the previous step to complete the proof of the theorem.arrow_forward2. Observations on the Wronskian. Suppose the functions y₁ and y2 are solutions to the differential equation p(x)y" + q(x)y' + r(x) y = 0 on an open interval I. 1. (a) Prove that if y₁ and y2 both vanish at the same point in I, then y₁ and y2 cannot form a fundamental set of solutions. 2. (b) Prove that if y₁ and y2 both attain a maximum or minimum at the same point in I, then y₁ and Y2 cannot form a fundamental set of solutions. 3. (c) show that the functions & and t² are linearly independent on the interval (−1, 1). Verify that both are solutions to the differential equation t² y″ – 2ty' + 2y = 0. Then justify why this does not contradict Abel's theorem. 4. (d) What can you conclude about the possibility that t and t² are solutions to the differential equation y" + q(x) y′ + r(x)y = 0?arrow_forwardQuestion 4 Find an equation of (a) The plane through the point (2, 0, 1) and perpendicular to the line x = y=2-t, z=3+4t. 3t, (b) The plane through the point (3, −2, 8) and parallel to the plane z = x+y. (c) The plane that contains the line x = 1+t, y = 2 − t, z = 4 - 3t and is parallel to the plane 5x + 2y + z = 1. (d) The plane that passes through the point (1,2,3) and contains the line x = 3t, y = 1+t, and z = 2-t. (e) The plane that contains the lines L₁: x = 1 + t, y = 1 − t, z = 2t and L2 : x = 2 − s, y = s, z = 2.arrow_forwardPlease find all values of x.arrow_forward3. Consider the initial value problem 9y" +12y' + 4y = 0, y(0) = a>0: y′(0) = −1. Solve the problem and find the value of a such that the solution of the initial value problem is always positive.arrow_forward5. Euler's equation. Determine the values of a for which all solutions of the equation 5 x²y" + axy' + y = 0 that have the form (A + B log x) x* or Ax¹¹ + Bä” tend to zero as a approaches 0.arrow_forward4. Problem on variable change. The purpose of this problem is to perform an appropriate change of variables in order to reduce the problem to a second-order equation with constant coefficients. ty" + (t² − 1)y'′ + t³y = 0, 0arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY