Elementary Technical Mathematics
11th Edition
ISBN: 9781285199191
Author: Dale Ewen, C. Robert Nelson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 13.2, Problem 1E
Using Illustration 1, find the measure of each acute angle for each right triangle:
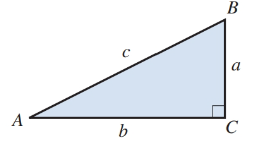
ILLUSTRATION 1
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(3) (16 points) Consider
z = uv,
u = x+y,
v=x-y.
(a) (4 points) Express z in the form z = fog where g: R² R² and f: R² →
R.
(b) (4 points) Use the chain rule to calculate Vz = (2, 2). Show all intermediate
steps otherwise no credit.
(c) (4 points) Let S be the surface parametrized by
T(x, y) = (x, y, ƒ (g(x, y))
(x, y) = R².
Give a parametric description of the tangent plane to S at the point p = T(x, y).
(d) (4 points) Calculate the second Taylor polynomial Q(x, y) (i.e. the quadratic
approximation) of F = (fog) at a point (a, b). Verify that
Q(x,y) F(a+x,b+y).
=
(6) (8 points) Change the order of integration and evaluate
(z +4ry)drdy .
So S√ ²
0
(10) (16 points) Let R>0. Consider the truncated sphere S given as
x² + y² + (z = √15R)² = R², z ≥0.
where F(x, y, z) = −yi + xj .
(a) (8 points) Consider the vector field
V (x, y, z) = (▼ × F)(x, y, z)
Think of S as a hot-air balloon where the vector field V is the velocity vector
field measuring the hot gasses escaping through the porous surface S. The flux
of V across S gives the volume flow rate of the gasses through S. Calculate
this flux.
Hint: Parametrize the boundary OS. Then use Stokes' Theorem.
(b) (8 points) Calculate the surface area of the balloon. To calculate the surface
area, do the following:
Translate the balloon surface S by the vector (-15)k. The translated
surface, call it S+ is part of the sphere x² + y²+z² = R².
Why do S and S+ have the same area?
⚫ Calculate the area of S+. What is the natural spherical parametrization
of S+?
Chapter 13 Solutions
Elementary Technical Mathematics
Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Prob. 5ECh. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Prob. 7ECh. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Prob. 9ECh. 13.1 - Refer to right triangle ABC in Illustration 1 for...
Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 13ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 15ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 17ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 20ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 23ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Prob. 27ECh. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Prob. 29ECh. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Prob. 31ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 33ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 37ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 41ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 43ECh. 13.1 - Prob. 44ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 46ECh. 13.1 - Prob. 47ECh. 13.1 - Prob. 48ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 51ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 53ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 55ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 57ECh. 13.1 - Prob. 58ECh. 13.1 - Prob. 59ECh. 13.1 - Prob. 60ECh. 13.1 - Prob. 61ECh. 13.1 - Prob. 62ECh. 13.1 - Find each angle rounded to the nearest hundredth...Ch. 13.1 - Prob. 64ECh. 13.1 - Find each angle rounded to the nearest hundredth...Ch. 13.1 - Prob. 66ECh. 13.1 - Find each angle rounded to the nearest hundredth...Ch. 13.1 - Prob. 68ECh. 13.1 - Prob. 69ECh. 13.1 - Prob. 70ECh. 13.1 - Prob. 71ECh. 13.1 - Prob. 72ECh. 13.1 - Prob. 73ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 5ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 7ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 9ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 17ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 19ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 21ECh. 13.2 - Prob. 22ECh. 13.2 - Prob. 23ECh. 13.2 - Prob. 24ECh. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Prob. 11ECh. 13.3 - Prob. 12ECh. 13.3 - Prob. 13ECh. 13.3 - Prob. 14ECh. 13.3 - Prob. 15ECh. 13.3 - Prob. 16ECh. 13.3 - Prob. 17ECh. 13.3 - Prob. 18ECh. 13.3 - Prob. 19ECh. 13.3 - Prob. 20ECh. 13.3 - Prob. 21ECh. 13.3 - Prob. 22ECh. 13.3 - Prob. 23ECh. 13.3 - Prob. 24ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 3ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 9ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 11ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 13ECh. 13.4 - Prob. 14ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 16ECh. 13.4 - Prob. 17ECh. 13.4 - Prob. 18ECh. 13.4 - Prob. 19ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 21ECh. 13.4 - Prob. 22ECh. 13.4 - Prob. 23ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.5 - A conveyor is used to lift paper to a shredder....Ch. 13.5 - A bullet is found embedded in the wall of a room...Ch. 13.5 - The recommended safety angle of a ladder against a...Ch. 13.5 - A piece of conduit 38.0 ft long is placed across...Ch. 13.5 - Find the width of the river in Illustration 4....Ch. 13.5 - Prob. 7ECh. 13.5 - A smokestack is 180 ft high. A guy wire must be...Ch. 13.5 - A railroad track has an angle of elevation of 1.0....Ch. 13.5 - Prob. 10ECh. 13.5 - Enrico has to draft a triangular roof to a house....Ch. 13.5 - A small plane takes off from an airport and begins...Ch. 13.5 - A gauge is used to check the diameter of a crank-...Ch. 13.5 - Round metal duct runs alongside some stairs from...Ch. 13.5 - The cables attached to a TV relay tower are 110 m...Ch. 13.5 - Prob. 16ECh. 13.5 - Prob. 17ECh. 13.5 - Prob. 18ECh. 13.5 - Use the right triangle in Illustration 13: a. Find...Ch. 13.5 - Prob. 20ECh. 13.5 - Twelve equally spaced holes must be drilled on a...Ch. 13.5 - Dimension x in the dovetail shown in Illustration...Ch. 13.5 - Find angle of the taper in Illustration 17....Ch. 13.5 - You need to use a metal screw with a head angle of...Ch. 13.5 - Prob. 25ECh. 13.5 - Prob. 26ECh. 13.5 - Find length x and angle A in Illustration 21....Ch. 13.5 - From the base of a building, measure out a...Ch. 13.5 - A mechanical draftsperson needs to find the...Ch. 13.5 - Prob. 30ECh. 13.5 - Prob. 31ECh. 13.5 - Prob. 32ECh. 13.5 - Solar heating and electric panels should face the...Ch. 13.5 - A lean-to is a simple shelter with three walls, a...Ch. 13 - For Exercises 1-7, see Illustration 1....Ch. 13 - For Exercises 1-7, see Illustration 1....Ch. 13 - Prob. 3RCh. 13 - For Exercises 1-7, see Illustration 1....Ch. 13 - Prob. 5RCh. 13 - Prob. 6RCh. 13 - Prob. 7RCh. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find angle A in Illustration 2. ILLUSTRATION 2Ch. 13 - Find angle B in Illustration 2. ILLUSTRATION 2Ch. 13 - Find side b in Illustration3. ILLUSTRATION 3Ch. 13 - Prob. 17RCh. 13 - Prob. 18RCh. 13 - Solve each right triangle:Ch. 13 - Prob. 20RCh. 13 - A satellite is directly overhead one observer...Ch. 13 - A ranger at the top of a fire tower observes the...Ch. 13 - Find the angle of slope of the symmetrical roof in...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find angle B Illustration 1. ILLUSTRATION 1Ch. 13 - Find side a Illustration 1. ILLUSTRATION 1Ch. 13 - Find side c Illustration 1. ILLUSTRATION 1Ch. 13 - Find angle A Illustration 2. ILLUSTRATION 2Ch. 13 - Find angle B Illustration 2. ILLUSTRATION 2Ch. 13 - Find side b Illustration 2. ILLUSTRATION 2Ch. 13 - A tower 50.0 ft high has a guy wire that is...Ch. 13 - Find length x in the retaining wall in...Ch. 13 - Find angle A in the retaining wall in Illustration...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- (1) (8 points) Let c(t) = (et, et sint, et cost). Reparametrize c as a unit speed curve starting from the point (1,0,1).arrow_forward(9) (16 points) Let F(x, y, z) = (x² + y − 4)i + 3xyj + (2x2 +z²)k = - = (x²+y4,3xy, 2x2 + 2²). (a) (4 points) Calculate the divergence and curl of F. (b) (6 points) Find the flux of V x F across the surface S given by x² + y²+2² = 16, z ≥ 0. (c) (6 points) Find the flux of F across the boundary of the unit cube E = [0,1] × [0,1] x [0,1].arrow_forward(8) (12 points) (a) (8 points) Let C be the circle x² + y² = 4. Let F(x, y) = (2y + e²)i + (x + sin(y²))j. Evaluate the line integral JF. F.ds. Hint: First calculate V x F. (b) (4 points) Let S be the surface r² + y² + z² = 4, z ≤0. Calculate the flux integral √(V × F) F).dS. Justify your answer.arrow_forward
- Determine whether the Law of Sines or the Law of Cosines can be used to find another measure of the triangle. a = 13, b = 15, C = 68° Law of Sines Law of Cosines Then solve the triangle. (Round your answers to four decimal places.) C = 15.7449 A = 49.9288 B = 62.0712 × Need Help? Read It Watch Itarrow_forward(4) (10 points) Evaluate √(x² + y² + z²)¹⁄² exp[}(x² + y² + z²)²] dV where D is the region defined by 1< x² + y²+ z² ≤4 and √√3(x² + y²) ≤ z. Note: exp(x² + y²+ 2²)²] means el (x²+ y²+=²)²]¸arrow_forward(2) (12 points) Let f(x,y) = x²e¯. (a) (4 points) Calculate Vf. (b) (4 points) Given x directional derivative 0, find the line of vectors u = D₁f(x, y) = 0. (u1, 2) such that the - (c) (4 points) Let u= (1+3√3). Show that Duƒ(1, 0) = ¦|▼ƒ(1,0)| . What is the angle between Vf(1,0) and the vector u? Explain.arrow_forward
- Find the missing values by solving the parallelogram shown in the figure. (The lengths of the diagonals are given by c and d. Round your answers to two decimal places.) a b 29 39 66.50 C 17.40 d 0 54.0 126° a Ꮎ b darrow_forwardAnswer the following questions related to the following matrix A = 3 ³).arrow_forward(5) (10 points) Let D be the parallelogram in the xy-plane with vertices (0, 0), (1, 1), (1, 1), (0, -2). Let f(x,y) = xy/2. Use the linear change of variables T(u, v)=(u,u2v) = (x, y) 1 to calculate the integral f(x,y) dA= 0 ↓ The domain of T is a rectangle R. What is R? |ǝ(x, y) du dv. |ð(u, v)|arrow_forward
- 2 Anot ined sove in peaper PV+96252 Q3// Find the volume of the region between the cylinder z = y2 and the xy- plane that is bounded by the planes x=1, x=2,y=-2,andy=2. vertical rect a Q4// Draw and Evaluate Soxy-2sin (ny2)dydx D Lake tarrow_forwardDetermine whether the Law of Sines or the Law of Cosines can be used to find another measure of the triangle. B 13 cm 97° Law of Sines Law of Cosines A 43° Then solve the triangle. (Round your answers to two decimal places.) b = x C = A = 40.00arrow_forward13' - 3π 2 < u <- π and tan v 5 14) Find the exact value given that sin u = a) sin(u-v) b) cos(u+v) c) tan(u-v) d) cos(2u) == √³, 1 < v < π.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License