Chapter 13.1, Problem 9P

Two gorgeous polyhedra can be created by stellating an icosahedron and a dodecahedron. SteI/ating means making starlike. Imagine turning each face of an icosahedron into a “star point"-namely, a pyramid whose base is a triangular face of th icosahedron. Likewise, imagine turning each face of a dodecahedron into a star point-namely, a pyramid whose base is a pentagonal face of the dodecahedron. A stellated icosahedron will then have 20 star points, whereas a stellated dodecahedron will have 12 star points.

a. Make 20 copies of Figure 13.15 on card stock. Cut, fold, and tape them to make 20 triangle-based pyramid star points. (The pattern makes star-point pyramids that don’t have bases.) Tape the star points together as though you were making an icosahedron out of their (open) bases.

 

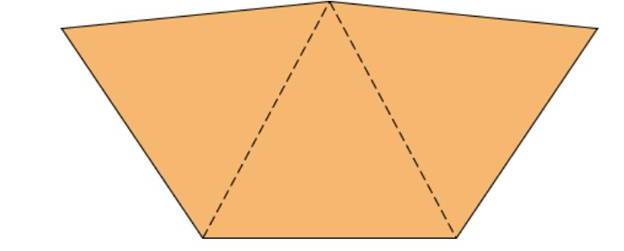
 Figure 13.15 Pattern for a star point of an icosahedron.

b. Make 12 copies of Figure 13.16 on card stock. Cut, fold, and tape them to make 12 pentagon-based pyramid star points. (The pattern makes star point pyramids that don’t have bases.) Tape the star points together as though you were making a dodecahedron out of their (open) bases.

 

 Figure 13.16 pattern for a star point of a dodecahedron