Chapter 13, Problem 9P

(a)

To determine

Prove that the generated far-field expressions for a thin dipole of length $\mathcal{l}$ carrying sinusoidal current $I_{\text{o}}\cos \beta z$ are $H_{\varphi s}=\frac{j{I}_{\text{o}}{e}^{-\beta r}}{2\pi r}\frac{\cos \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)-\cos \frac{\beta \mathcal{l}}{2}}{\sin \theta }$, and $E_{\theta s}=\eta H_{\varphi s}$.

Explanation of Solution

Calculation:

Consider the mentioned equation given in the textbook,

$d{A}_{zs}=\frac{\mu I_{\text{o}}\cos \beta zdz}{4\pi r\text{'}}{e}^{-j\beta r\text{'}}$        (1)

Refer to the mentioned Figure given in the textbook, the integration limits must be $\pm \frac{\mathcal{l}}{2}$.

$A_{zs}=\frac{\mu I_{\text{o}}}{4\pi r}{\displaystyle {\int }_{-\frac{\mathcal{l}}{2}}^{\frac{\mathcal{l}}{2}}{e}^{-j\beta \left(r-z\cos \theta \right)}\cos \beta zdz}\left\{\because r\text{'}=r-z\cos \theta \right\}$

$A_{zs}=\frac{\mu I_{\text{o}}}{4\pi r}{e}^{-j\beta r}{\displaystyle {\int }_{-\frac{\mathcal{l}}{2}}^{\frac{\mathcal{l}}{2}}{e}^{j\beta z\cos \theta }\cos \beta zdz}$        (2)

Refer to the integral tables of Appendix A.8,

${\displaystyle \int e^{az}\cos bzdz}=\frac{e^{az}\left(a\cos bz+b\sin bz\right)}{a^2+b^2}+c$        (3)

Apply equation (3) in (2),

$\begin{array}{c}{A}_{zs}={\frac{\mu I_{\text{o}}{e}^{-j\beta r}{e}^{-j\beta z\cos \theta }}{4\pi r}\frac{\left(j\beta \cos \theta \cos \beta z+\beta \sin \beta z\right)}{-{\beta }^2{\cos }^2\theta +{\beta }^2}|}_{-\frac{\mathcal{l}}{2}}^{\frac{\mathcal{l}}{2}}\\ ={\frac{\mu I_{\text{o}}{e}^{-j\beta r}{e}^{-j\beta z\cos \theta }}{4\pi r}\frac{\left(j\cos \theta \cos z+\sin \beta z\right)}{\beta \left(1-{\cos }^2\theta \right)}|}_{-\frac{\mathcal{l}}{2}}^{\frac{\mathcal{l}}{2}}\\ ={\frac{\mu I_{\text{o}}{e}^{-j\beta r}{e}^{-j\beta z\cos \theta }}{4\pi r}\frac{\left(j\cos \theta \cos z+\sin \beta z\right)}{\beta \left({\sin }^2\theta \right)}|}_{-\frac{\mathcal{l}}{2}}^{\frac{\mathcal{l}}{2}}\left\{\because 1-{\cos }^2\theta ={\sin }^2\theta \right\}\\ ={\frac{\mu I_{\text{o}}{e}^{-j\beta r}\left[\cos \left(\beta z\cos \theta \right)-j\sin \left(\beta z\cos \theta \right)\right]}{4\pi r}\frac{\left(j\cos \theta \cos z+\sin \beta z\right)}{\beta \left({\sin }^2\theta \right)}|}_{-\frac{\mathcal{l}}{2}}^{\frac{\mathcal{l}}{2}}\end{array}$

Applying the limits to the above equation as follows,

$A_{zs}=\frac{\mu I_{\text{o}}{e}^{-j\beta r}}{4\pi r}\frac{1}{\beta {\sin }^2\theta }\left[\sin \frac{\beta \mathcal{l}}{2}\cos \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)-\cos \theta \cos \frac{\beta \mathcal{l}}{2}\sin \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)\right]$

Consider the general relationship between magnetic flux density and magnetic field intensity.

$B_s=\mu H_s=\nabla \times A_s$

Rearrange the equation as follows,

$H_{\varphi s}=\frac{1}{\mu }\left(\nabla \times A_s\right)$

$H_{\varphi s}=\frac{1}{\mu r}\left[\frac{\partial }{\partial r}\left(r{A}_{\theta }\right)-\frac{\partial A_r}{\partial \theta }\right]$        (4)

Where, $A_{\theta }=-A_z\sin \theta$ and $A_r=A_z\cos \theta$.

Therefore, equation (4) can be rewritten as follows,

$H_{\varphi s}=\left\{\begin{array}{l}\frac{I_{\text{o}}}{2\pi r}\frac{e^{-j\beta r}}{\beta }\left(\frac{j\beta }{\sin \theta }\right)\left[\sin \frac{\beta \mathcal{l}}{2}\cos \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)-\cos \theta \cos \frac{\beta \mathcal{l}}{2}\sin \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)\right]+\\ \frac{I_{\text{o}}}{2\pi r^2}{e}^{-j\beta r}\left(\sin \frac{\beta \mathcal{l}}{2}\cos \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)-\cos \theta \cos \frac{\beta \mathcal{l}}{2}\sin \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)\right)\end{array}\right\}$

Consider for a far-field expression, only $\frac{1}{r}$ terms remains. Therefore, above expression becomes,

$H_{\varphi s}=\frac{j{I}_{\text{o}}{e}^{-j\beta r}}{2\pi r}\left[\frac{\sin \frac{\beta \mathcal{l}}{2}\cos \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)-\cos \theta \cos \frac{\beta \mathcal{l}}{2}\sin \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)}{\sin \theta }\right]$

and the relationship between electric field intensity and magnetic field intensity is,

$E_{\theta s}=\eta H_{\varphi s}$

Conclusion:

Thus, the generated far-field expressions for a thin dipole of length $\mathcal{l}$ carrying sinusoidal current $I_{\text{o}}\cos \beta z$ are $H_{\varphi s}=\frac{j{I}_{\text{o}}{e}^{-\beta r}}{2\pi r}\frac{\cos \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)-\cos \frac{\beta \mathcal{l}}{2}}{\sin \theta }$, and $E_{\theta s}=\eta H_{\varphi s}$ is proved.

(b)

To determine

Sketch the group pattern $f\left(\theta \right)$ in Part (a) for $\mathcal{l}=\lambda ,\frac{3\lambda }{2},\text{and}2\lambda$.

Answer to Problem 9P

The group pattern $f\left(\theta \right)$ in Part (a) for $\mathcal{l}=\lambda ,\frac{3\lambda }{2},\text{and}2\lambda$ is plotted.

Explanation of Solution

Calculation:

Refer to Part (a),

$H_{\varphi s}=\frac{j{I}_{\text{o}}{e}^{-j\beta r}}{2\pi r}\left[\frac{\sin \frac{\beta \mathcal{l}}{2}\cos \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)-\cos \theta \cos \frac{\beta \mathcal{l}}{2}\sin \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)}{\sin \theta }\right]$

From the above expression, the group pattern is,

$f\left(\theta \right)=\frac{\cos \left(\frac{\beta \mathcal{l}}{2}\cos \theta \right)-\cos \frac{\beta \mathcal{l}}{2}}{\sin \theta }$        (5)

Consider the expression for the phase constant.

$\beta =\frac{2\pi }{\lambda }$

Here,

$\lambda$ is the wavelength.

For $\mathcal{l}=\lambda$:

Substitute $\frac{2\pi }{\lambda }$ for $\beta$ and $\lambda$ for $\mathcal{l}$ in equation (5).

$\begin{array}{c}f\left(\theta \right)=\frac{\cos \left(\frac{\left(\frac{2\pi }{\lambda }\right)\lambda }{2}\cos \theta \right)-\cos \frac{\left(\frac{2\pi }{\lambda }\right)\lambda }{2}}{\sin \theta }\\ =\frac{\cos \left(\pi \cos \theta \right)-\cos \pi }{\sin \theta }\\ =\frac{\cos \left(\pi \cos \theta \right)+1}{\sin \theta }\end{array}$

MATLAB code to plot the group pattern $f\left(\theta \right)$ for $\mathcal{l}=\lambda$.

theta=-360:pi./180:360;

c_n1=(cos(pi.*cos(theta)))+1;

s_n1=sin(theta);

f1=abs(c_n1./s_n1);

polar(theta,f1)

MATLAB output:

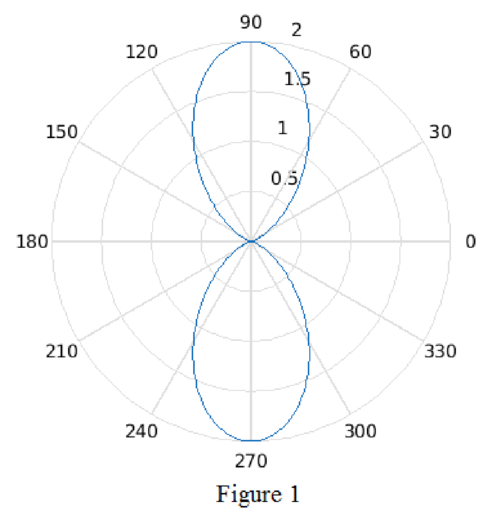
Figure 1 shows the polar plot for the group pattern $f\left(\theta \right)$ for $\mathcal{l}=\lambda$.

For $\mathcal{l}=\frac{3\lambda }{2}$:

Substitute $\frac{2\pi }{\lambda }$ for $\beta$ and $\frac{3\lambda }{2}$ for $\mathcal{l}$ in equation (5).

$\begin{array}{c}f\left(\theta \right)=\frac{\cos \left(\frac{\left(\frac{2\pi }{\lambda }\right)\left(\frac{3\lambda }{2}\right)}{2}\cos \theta \right)-\cos \frac{\left(\frac{2\pi }{\lambda }\right)\left(\frac{3\lambda }{2}\right)}{2}}{\sin \theta }\\ =\frac{\cos \left(\frac{3\pi }{2}\cos \theta \right)-\cos \frac{3\pi }{2}}{\sin \theta }\\ =\frac{\cos \left(\frac{3\pi }{2}\cos \theta \right)}{\sin \theta }\end{array}$

MATLAB code to plot the group pattern $f\left(\theta \right)$ for $\mathcal{l}=\frac{3\lambda }{2}$.

theta=-360:pi./180:360;

c_n2=cos((3.*pi./2).*cos(theta));

s_n2=sin(theta);

f2=abs(c_n2./s_n2);

polar(theta,f2)

MATLAB output:

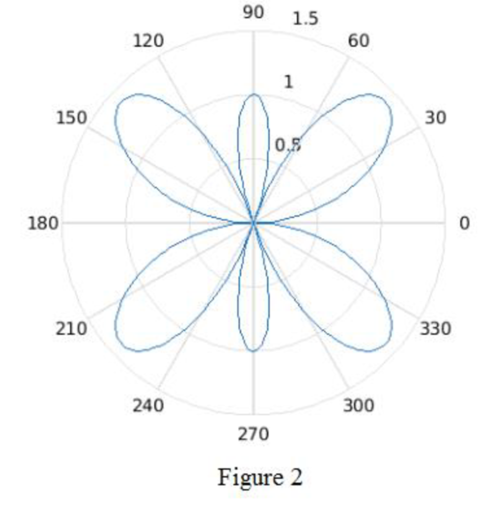
Figure 2 shows the polar plot for the group pattern $f\left(\theta \right)$ for $\mathcal{l}=\frac{3\lambda }{2}$.

For $\mathcal{l}=2\lambda$:

Substitute $\frac{2\pi }{\lambda }$ for $\beta$ and $2\lambda$ for $\mathcal{l}$ in equation (5).

$\begin{array}{c}f\left(\theta \right)=\frac{\cos \left(\frac{\left(\frac{2\pi }{\lambda }\right)\left(2\lambda \right)}{2}\cos \theta \right)-\cos \frac{\left(\frac{2\pi }{\lambda }\right)\left(2\lambda \right)}{2}}{\sin \theta }\\ =\frac{\cos \left(2\pi \cos \theta \right)-\cos 2\pi }{\sin \theta }\\ =\frac{\cos \left(2\pi \cos \theta \right)-1}{\sin \theta }\end{array}$

MATLAB code to plot the group pattern $f\left(\theta \right)$ for $\mathcal{l}=2\lambda$.

theta=-360:pi./180:360;

c_n3=cos(2.*pi.*cos(theta))-1;

s_n3=sin(theta);

f3=abs(c_n3./s_n3);

polar(theta,f3)

MATLAB output:

Figure 3 shows the polar plot for the group pattern $f\left(\theta \right)$ for $\mathcal{l}=\frac{3\lambda }{2}$.

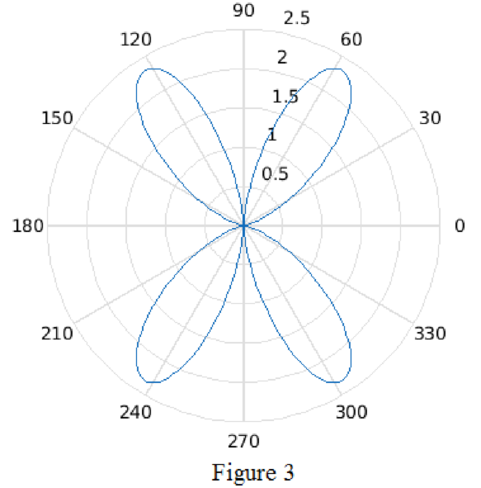
Conclusion:

Thus, the group pattern $f\left(\theta \right)$ in Part (a) for $\mathcal{l}=\lambda ,\frac{3\lambda }{2},\text{and}2\lambda$ is plotted.