Calculus, Early Transcendentals
9th Edition
ISBN: 9781337613927
Author: Stewart
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 13, Problem 5PP
A ball rolls off a table with a speed of 2 ft/s. The table is 3.5 ft high.
(a) Determine the point at which the ball hits the floor and find its speed at the instant of impact.
(b) Find the angle θ between the path of the ball and the vertical line drawn through the point of impact (see the figure).
(c) Suppose the hall rebounds from the floor at the same angle with which it hits the floor, but loses 20% of its speed due to energy absorbed by the ball on impact. Where does the ball strike the floor on the second bounce?
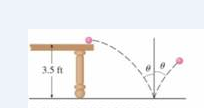
FIGURE FOR PROBLEM 5
Expert Solution & Answer
Trending nowThis is a popular solution!
Learn your wayIncludes step-by-step video
schedule10:04
Chapter 13 Solutions
Calculus, Early Transcendentals
Ch. 13.1 - Prob. 1ECh. 13.1 - Prob. 2ECh. 13.1 - Find the limit. 3. limt0(e3ti+t2sin2tj+cos2tk)Ch. 13.1 - Find the limit. 4. limt1(t2-tt-1i+t+8j+sintlntk)Ch. 13.1 - Find the limit. 5. limt1+t21t2,tan-1t,1e2ttCh. 13.1 - Prob. 6ECh. 13.1 - Prob. 7ECh. 13.1 - Prob. 8ECh. 13.1 - Prob. 9ECh. 13.1 - Prob. 10E
Ch. 13.1 - Prob. 11ECh. 13.1 - Prob. 12ECh. 13.1 - Prob. 13ECh. 13.1 - Prob. 14ECh. 13.1 - Prob. 15ECh. 13.1 - Prob. 16ECh. 13.1 - Draw the projection of the curve onto the given...Ch. 13.1 - Prob. 18ECh. 13.1 - Prob. 19ECh. 13.1 - Prob. 20ECh. 13.1 - Prob. 21ECh. 13.1 - Prob. 22ECh. 13.1 - Find a vector equation and parametric equations...Ch. 13.1 - Find a vector equation and parametric equations...Ch. 13.1 - Match the parametric equations with the graphs...Ch. 13.1 - Match the parametric equations with the graphs...Ch. 13.1 - Match the parametric equations with the graphs...Ch. 13.1 - Match the parametric equations with the graphs...Ch. 13.1 - Match the parametric equations with the graphs...Ch. 13.1 - Match the parametric equations with the graphs...Ch. 13.1 - Prob. 31ECh. 13.1 - Prob. 32ECh. 13.1 - Prob. 33ECh. 13.1 - Prob. 34ECh. 13.1 - Prob. 35ECh. 13.1 - Show that the curve with parametric equations x =...Ch. 13.1 - Find three different surfaces that contain the...Ch. 13.1 - Find three different surfaces that contain the...Ch. 13.1 - Prob. 39ECh. 13.1 - At what points does the helix r(t) = sin t, cos t,...Ch. 13.1 - Graph the curve with parametric equations x = sin...Ch. 13.1 - Graph the curve with parametric equations x = (1 +...Ch. 13.1 - Prob. 48ECh. 13.1 - Show that the curve with parametric equations x =...Ch. 13.1 - Prob. 50ECh. 13.1 - Prob. 51ECh. 13.1 - Prob. 52ECh. 13.1 - Prob. 53ECh. 13.1 - Prob. 54ECh. 13.1 - Prob. 55ECh. 13.1 - Prob. 56ECh. 13.1 - Prob. 57ECh. 13.1 - Prob. 58ECh. 13.1 - Properties of Limits Suppose u and v are vector...Ch. 13.2 - Prob. 1ECh. 13.2 - Prob. 2ECh. 13.2 - (a) Sketch the plane curve with the given vector...Ch. 13.2 - Prob. 4ECh. 13.2 - (a) Sketch the plane curve with the given vector...Ch. 13.2 - (a) Sketch the plane curve with the given vector...Ch. 13.2 - Prob. 7ECh. 13.2 - Prob. 8ECh. 13.2 - Find the derivative of the vector function. 9....Ch. 13.2 - Prob. 10ECh. 13.2 - Find the derivative of the vector function. 11....Ch. 13.2 - Prob. 12ECh. 13.2 - Prob. 13ECh. 13.2 - Prob. 14ECh. 13.2 - Prob. 15ECh. 13.2 - Prob. 16ECh. 13.2 - Prob. 17ECh. 13.2 - Prob. 18ECh. 13.2 - Prob. 19ECh. 13.2 - Prob. 20ECh. 13.2 - Find the unit tangent vector T(t) at the given...Ch. 13.2 - Find the unit tangent vector T(t) at the given...Ch. 13.2 - Prob. 23ECh. 13.2 - Find the unit tangent vector T(t) at the given...Ch. 13.2 - Prob. 25ECh. 13.2 - Prob. 26ECh. 13.2 - Prob. 27ECh. 13.2 - Find parametric equations for the tangent line to...Ch. 13.2 - Find a vector equation for the tangent line to the...Ch. 13.2 - Find the point on the curve r(t) = 2 cos t, 2 sin...Ch. 13.2 - Find parametric equations tor the tangent line to...Ch. 13.2 - Find parametric equations tor the tangent line to...Ch. 13.2 - Find parametric equations tor the tangent line to...Ch. 13.2 - (a) Find the point of intersection of the tangent...Ch. 13.2 - Prob. 35ECh. 13.2 - At what point do the curves r1(t) = t, 1 t, 3 +...Ch. 13.2 - Evaluate the integral. 35. 02(ti-t3j+3t5k)dtCh. 13.2 - Evaluate the integral. 36. 14(2t3/2i+(t+1)tk)dtCh. 13.2 - Evaluate the integral. 37....Ch. 13.2 - Evaluate the integral. 38....Ch. 13.2 - Evaluate the integral. 39....Ch. 13.2 - Evaluate the integral. 40. (te2ti+t1-tj+11-t2k)dtCh. 13.2 - Find r(t) if r'(t) = 2t i + 3t2 j + t k and r(1) =...Ch. 13.2 - Find r(t) if r'(t) = t i + et j + tet k and r(0) =...Ch. 13.2 - Prove Formula 1 of Theorem 3.Ch. 13.2 - Prove Formula 3 of Theorem 3.Ch. 13.2 - Prob. 47ECh. 13.2 - Prob. 48ECh. 13.2 - If u(t) = sin t, cos t, t) and v(t) = t, cos t,...Ch. 13.2 - Prob. 50ECh. 13.2 - Prob. 51ECh. 13.2 - Prob. 52ECh. 13.2 - Prob. 53ECh. 13.2 - Prob. 54ECh. 13.2 - Show that if r is a vector function such that r''...Ch. 13.2 - Prob. 56ECh. 13.2 - Prob. 57ECh. 13.2 - Prob. 58ECh. 13.2 - Prob. 59ECh. 13.2 - Prob. 60ECh. 13.3 - (a) Use Equation 2 to compute the length of the...Ch. 13.3 - Prob. 2ECh. 13.3 - Find the length of the curve. 1. r(t) =t, 3 cos t,...Ch. 13.3 - Find the length of the curve. 2. r(t)=2t,t2,13t3,...Ch. 13.3 - Find the length of the curve. 3. r(t)=2ti+etj+etk,...Ch. 13.3 - Find the length of the curve. 4. r(t) =cos t i +...Ch. 13.3 - Find the length of the curve. 5. r(t) = i + t2 j +...Ch. 13.3 - Find the length of the curve. 6. r(t) = t2 i + 9t...Ch. 13.3 - Find the length of the curve correct to four...Ch. 13.3 - Find the length of the curve correct to four...Ch. 13.3 - Find the length of the curve correct to four...Ch. 13.3 - Graph the curve with parametric equations x = sin...Ch. 13.3 - Let C be the curve of intersection of the...Ch. 13.3 - Find, correct to four decimal places, the length...Ch. 13.3 - Prob. 15ECh. 13.3 - Prob. 16ECh. 13.3 - Suppose you start at the point (0, 0. 3) and move...Ch. 13.3 - Reparametrize the curve r(t)=(2t2+11)i+2tt2+1j...Ch. 13.3 - (a) Find the unit tangent and unit normal vectors...Ch. 13.3 - (a) Find the unit tangent and unit normal vectors...Ch. 13.3 - (a) Find the unit tangent and unit normal vectors...Ch. 13.3 - (a) Find the unit tangent and unit normal vectors...Ch. 13.3 - (a) Find the unit tangent and unit normal vectors...Ch. 13.3 - (a) Find the unit tangent and unit normal vectors...Ch. 13.3 - Use Theorem 10 to find the curvature. 21. r(t) =...Ch. 13.3 - Use Theorem 10 to find the curvature. 22. r(t) = t...Ch. 13.3 - Use Theorem 10 to find the curvature. 23....Ch. 13.3 - Prob. 28ECh. 13.3 - Find the curvature of r(t) = t, t2, t3 at the...Ch. 13.3 - Graph the curve with parametric equations x = cos...Ch. 13.3 - Use Formula 11 to find the curvature. 27. y = x4...Ch. 13.3 - To find: The curvature of y=tanx using Formula 11....Ch. 13.3 - Use Formula 11 to find the curvature. 27. y = x4...Ch. 13.3 - At what point does the curve have maximum...Ch. 13.3 - At what point does the curve have maximum...Ch. 13.3 - Find an equation of a parabola that has curvature...Ch. 13.3 - (a) Is the curvature of the curve C shown in the...Ch. 13.3 - Prob. 38ECh. 13.3 - Prob. 39ECh. 13.3 - Prob. 41ECh. 13.3 - Prob. 42ECh. 13.3 - Prob. 43ECh. 13.3 - Prob. 44ECh. 13.3 - Prob. 45ECh. 13.3 - Prob. 46ECh. 13.3 - Curvature of Plane Parametric Curves The curvature...Ch. 13.3 - Curvature of Plane Parametric Curves The curvature...Ch. 13.3 - Prob. 49ECh. 13.3 - Consider the curvature at x = 0 for each member of...Ch. 13.3 - Prob. 51ECh. 13.3 - Prob. 52ECh. 13.3 - Find equations of the normal plane and osculating...Ch. 13.3 - Find equations of the normal plane and osculating...Ch. 13.3 - Find equations of the osculating circles of the...Ch. 13.3 - Prob. 56ECh. 13.3 - At what point on the curve x = t3, y = 3t, z = t4...Ch. 13.3 - Find equations of the normal and osculating planes...Ch. 13.3 - Prob. 60ECh. 13.3 - Prob. 61ECh. 13.3 - Prob. 62ECh. 13.3 - Show that the curvature is related to the tangent...Ch. 13.3 - Prob. 64ECh. 13.3 - Prob. 65ECh. 13.3 - Prob. 66ECh. 13.3 - Use Formula 14 to find the torsion at the given...Ch. 13.3 - Prob. 68ECh. 13.3 - Prob. 69ECh. 13.3 - Prob. 70ECh. 13.3 - Prob. 71ECh. 13.3 - Frenet-Serret Formulas The following formulas,...Ch. 13.3 - Show that the circular helix r(t)=acost,asint,bt ,...Ch. 13.3 - Find the curvature and torsion of the curve x =...Ch. 13.3 - The DNA molecule has the shape of a double helix...Ch. 13.4 - The table gives coordinates of a particle moving...Ch. 13.4 - Prob. 2ECh. 13.4 - Prob. 3ECh. 13.4 - Prob. 4ECh. 13.4 - Prob. 5ECh. 13.4 - Prob. 6ECh. 13.4 - Prob. 7ECh. 13.4 - Find the velocity, acceleration, and speed of a...Ch. 13.4 - Prob. 9ECh. 13.4 - Prob. 10ECh. 13.4 - Find the velocity, acceleration, and speed of a...Ch. 13.4 - Find the velocity, acceleration, and speed of a...Ch. 13.4 - Find the velocity, acceleration, and speed of a...Ch. 13.4 - Find the velocity and position vectors of a...Ch. 13.4 - Find the velocity and position vectors of a...Ch. 13.4 - Find the velocity and position vectors of a...Ch. 13.4 - The position function of a particle is given by...Ch. 13.4 - What force is required so that a particle of mass...Ch. 13.4 - A force with magnitude 20 N acts directly upward...Ch. 13.4 - Show that if a particle moves with constant speed,...Ch. 13.4 - A projectile is fired with an initial speed of 200...Ch. 13.4 - Rework Exercise 23 if the projectile is fired from...Ch. 13.4 - A ball is thrown at an angle of 45 to the ground....Ch. 13.4 - A projectile is tired from a tank with initial...Ch. 13.4 - A rifle is fired with angle of elevation 36. What...Ch. 13.4 - Prob. 28ECh. 13.4 - A medieval city has the shape of a square and is...Ch. 13.4 - Show that a projectile reaches three-quarters of...Ch. 13.4 - A ball is thrown eastward into the air from the...Ch. 13.4 - A ball with mass 0.8 kg is thrown southward into...Ch. 13.4 - Another reasonable model for the water speed of...Ch. 13.4 - Prob. 35ECh. 13.4 - (a) If a particle moves along a straight line,...Ch. 13.4 - Prob. 37ECh. 13.4 - Prob. 38ECh. 13.4 - Find the tangential and normal components of the...Ch. 13.4 - Prob. 40ECh. 13.4 - Find the tangential and normal components of the...Ch. 13.4 - Prob. 42ECh. 13.4 - The position function of a spaceship is...Ch. 13.4 - A rocket burning its onboard fuel while moving...Ch. 13.4 - Prob. 1APCh. 13.4 - Prob. 3APCh. 13 - Prob. 1CCCh. 13 - Prob. 2CCCh. 13 - Prob. 3CCCh. 13 - Prob. 4CCCh. 13 - Prob. 5CCCh. 13 - (a) What is the definition of curvature? (b) Write...Ch. 13 - Prob. 7CCCh. 13 - Prob. 8CCCh. 13 - State Keplers Laws.Ch. 13 - Prob. 1TFQCh. 13 - Prob. 2TFQCh. 13 - Prob. 3TFQCh. 13 - Prob. 4TFQCh. 13 - Prob. 5TFQCh. 13 - Prob. 6TFQCh. 13 - Prob. 7TFQCh. 13 - Determine whether the statement is true or false....Ch. 13 - Determine whether the statement is true or false....Ch. 13 - Prob. 10TFQCh. 13 - Prob. 11TFQCh. 13 - Determine whether the statement is true or false....Ch. 13 - Determine whether the statement is true or false....Ch. 13 - Prob. 14TFQCh. 13 - Prob. 15TFQCh. 13 - (a) Sketch the curve with vector function r(t) = t...Ch. 13 - Let r(t) = 2-t, (et 1)/t, ln(t + 1). (a) Find the...Ch. 13 - Prob. 3ECh. 13 - Find parametric equations for the tangent line to...Ch. 13 - If r(t) = t2 i + t cos t j + sin t k, evaluate...Ch. 13 - Prob. 6ECh. 13 - Prob. 7ECh. 13 - Prob. 8ECh. 13 - The helix r1(t) = cos t i + sin t j + t k...Ch. 13 - Prob. 10ECh. 13 - For the curve given by r(t) = sin3 t, cos3 t, sin2...Ch. 13 - Find the curvature of the ellipse x = 3 cos t, y =...Ch. 13 - Find the curvature of the curve y = x4 at the...Ch. 13 - Find an equation of the osculating circle of the...Ch. 13 - Find an equation of the osculating plane of the...Ch. 13 - The figure shows the curve C traced by a particle...Ch. 13 - A particle moves with position function r(t) = t...Ch. 13 - Find the velocity, speed, and acceleration of a...Ch. 13 - A particle starts at the origin with initial...Ch. 13 - An athlete throws a shot at an angle of 45 to the...Ch. 13 - A projectile is launched with an initial speed of...Ch. 13 - Prob. 22ECh. 13 - Prob. 23ECh. 13 - PROBLEM PLUS FIGURE FOR PROBLEM 1 1. A particle P...Ch. 13 - A projectile is fired from the origin with angle...Ch. 13 - (a) A projectile it fired from the origin down an...Ch. 13 - A ball rolls off a table with a speed of 2 ft/s....Ch. 13 - Find the curvature of the curve with parametric...Ch. 13 - If a projectile is fired with angle of elevation ...Ch. 13 - A cable has radius r and length L and is wound...Ch. 13 - Prob. 9PP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- A gear train consists of three gears meshed together (Figure 9). The middle gear is known as an idler. Show that the angular velocity of the third gear does not depend on the number of teeth of the idler gear (Gear 2).arrow_forwardObject A is travelling along a circle of radius 2, and Object B is travelling along a circle of radius 5. The object have the same angular speed. Do the objects have the same linear speed? If not, which object has the greater linear speed?arrow_forwardA goat is tethered to a barn by a 12-ft chain. If the chain is connected to the barn at a point 6 ft from one end of the barn, what is the area of the pasture that the goat is able to graze?arrow_forward
- A two-stage gear train consists of four gears meshed together (Figure 10). The second and third gears are attached, so that they share the same angular velocity (2=4). Find a formula giving the angular velocity of the fourth gear, 2, in terms of 1 and the values of n1,n2,n3andn4.arrow_forwardWhich A winch of radius 2 ft is used to lift heavy loads. If the winch makes 8 revolutions every 15 s, find the speed at which the load is rising.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Evaluating Indefinite Integrals; Author: Professor Dave Explains;https://www.youtube.com/watch?v=-xHA2RjVkwY;License: Standard YouTube License, CC-BY
Calculus - Lesson 16 | Indefinite and Definite Integrals | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=bMnMzNKL9Ks;License: Standard YouTube License, CC-BY