Chapter 13, Problem 3PP

A projectile is fired from the origin with angle of elevation α and initial speed v₀. Assuming that air resistance is negligible and that the only force acting on the projectile is gravity, g. we showed m Example 13.4.5 that the position vector of the projectile is

$r\left(t\right)=\left(v_0\cos \alpha \right)ti\text{ + }\left[\left(v_0\sin \alpha \right)t-\frac{1}{2}g{t}^2\right]j$

We also showed that the maximum horizontal distance of the projectile is achieved when α = 45° and in this case the range is. $R=v_0^2/g$.

(a) At what angle should the projectile he tired to achieve maximum height and what is the maximum height?

(b) Fix the initial speed is r₀ and consider the parabola x₂ + 2Ry – R² = 0, whose graph is shown in the figure at the left Show that the projectile can hit any target inside or on the boundary of the region hounded by the parabola and the x-axis, and that it can't hit any target outside this region.

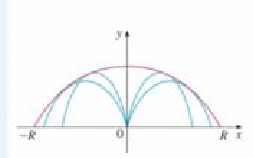
FIGURE FOR PROBLEM 3

(c) Suppose that the gun is elevated to an angle of inclination α in order to aim at a target that is suspended at a height h directly over a point D units downrange (sec the figure below). The target is released at the instant the gun is fired. Show that the projectile always hits the target, regardless of the value v₀, provided the projectile docs not hit the ground “before” D.