EP INTRODUCTORY STATISTICS-MYSTATLAB
3rd Edition
ISBN: 9780135190210
Author: Gould
Publisher: PEARSON CO
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13, Problem 35SE
Rainfall In a well-known study on the effects of cloud seeding to produce rainfall (cited on page 659 of the text by Simpson et. al), experimenters randomly assigned airplanes to release either silver nitrate (which is believed to increase the amount of rainfall from a cloud) or a placebo. Fifty-two clouds were chosen at random; half were “seeded” with silver nitrate, and half were not. In the text, we compared the
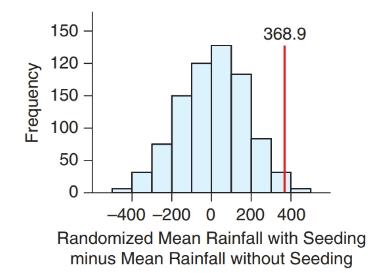
In the study, the seeded clouds produced more rain, on average, by 368.9 acre-feet. To determine whether such differences could occur by chance, a statistician could have written the 52 rainfall amounts on separate slips of paper and randomly dealt them into two stacks. He or she would then have computed the mean of each stack and found the difference. This was actually done by a computer and repeated 1000 times. The results are shown in the histogram.
Carry out a hypothesis test to determine whether cloud seeding increased the mean rainfall. By referring to the histogram, choose from the following possible p-values (one-tailed):
0.50, 0.25, 0.15, 0.025, less than 0.0001
Use a 5% significance level for your test.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Business
https://www.hawkeslearning.com/Statistics/dbs2/datasets.html
NC Current Students - North Ce X | NC Canvas Login Links - North ( X
Final Exam Comprehensive x Cengage Learning
x
WASTAT - Final Exam - STAT
→
C
webassign.net/web/Student/Assignment-Responses/submit?dep=36055360&tags=autosave#question3659890_9
Part (b)
Draw a scatter plot of the ordered pairs.
N
Life
Expectancy
Life
Expectancy
80
70
600
50
40
30
20
10
Year of
1950
1970 1990
2010 Birth
O
Life
Expectancy
Part (c)
800
70
60
50
40
30
20
10
1950
1970 1990
W
ALT
林
$
#
4
R
J7
Year of
2010 Birth
F6
4+
80
70
60
50
40
30
20
10
Year of
1950 1970 1990
2010 Birth
Life
Expectancy
Ox
800
70
60
50
40
30
20
10
Year of
1950 1970 1990 2010 Birth
hp
P.B.
KA
&
7
80
% 5
H
A
B
F10
711
N
M
K
744
PRT SC
ALT
CTRL
Chapter 13 Solutions
EP INTRODUCTORY STATISTICS-MYSTATLAB
Ch. 13 - What is the fundamental condition required for...Ch. 13 - In what situations are nonparametric statistics...Ch. 13 - In addition to random samples, what other...Ch. 13 - What summary statistics are best used to report...Ch. 13 - Prob. 5SECh. 13 - Prob. 6SECh. 13 - Prob. 7SECh. 13 - Log Transforms a. Find the log (base 10) of each...Ch. 13 - Prob. 9SECh. 13 - Prob. 10SE
Ch. 13 - Prob. 11SECh. 13 - Morning Routine A statistics student conducted a...Ch. 13 - Exercise Hours A statistics student was interested...Ch. 13 - Television Viewing A Nielsen poll asked people the...Ch. 13 - Lead Exposure (Example 3) Excessive lead levels...Ch. 13 - Juvenile Delinquents Dr. Kirkland R. Gable (in...Ch. 13 - The Stroop Effect Suppose you had to identify the...Ch. 13 - Reading Material on Colored Paper In the past,...Ch. 13 - Males’ Pulse Rates Students in a statistics class...Ch. 13 - Females’ Pulse Rates Refer to exercise 13.19. This...Ch. 13 - Ages of Brides and Grooms A random sample of the...Ch. 13 - Textbook Prices A student was interested in...Ch. 13 - Meat-Eating Behavior (Example 4) A researcher was...Ch. 13 - Credit Card Debt A statistics student who was...Ch. 13 - Prob. 25SECh. 13 - Sleep Typically, do men and women sleep different...Ch. 13 - Cell Phone Bills Cell phone bills (rounded to the...Ch. 13 - Weights of Athletes Data were collected on the...Ch. 13 - Happiness A StatCrunch survey of happiness...Ch. 13 - Soda A StatCrunch survey was done asking what...Ch. 13 - Sports and Extraversion (Example 5) Are students...Ch. 13 - Happiness Are women happier than men? A StatCrunch...Ch. 13 - College Students and Credit Card Debt In exercise...Ch. 13 - Soda Does soda constitute a larger part of the...Ch. 13 - Rainfall In a well-known study on the effects of...Ch. 13 - Rainfall Refer to exercise 13.35, which discussed...Ch. 13 - Randomization Exercise 13.35 describes a...Ch. 13 - Randomization Exercise 13.35 describes a...Ch. 13 - Prob. 39CRECh. 13 - For exercises 13.39 through 13.46, choose from the...Ch. 13 - Prob. 41CRECh. 13 - For exercises 13.39 through 13.46, choose from the...Ch. 13 - Prob. 43CRECh. 13 - Prob. 44CRECh. 13 - For exercises 13.39 through 13.46, choose from the...Ch. 13 - For exercises 13.39 through 13.46, choose from the...Ch. 13 - Ice Cream Cones McDonald’s claims that its ice...Ch. 13 - Average Body Temperatures Many people believe that...Ch. 13 - Contacting Mom Random samples of 30 professors of...Ch. 13 - 13.50 through 13.54 Texts Sent and Received...Ch. 13 - 13.50 through 13.54 Texts Sent and Received...Ch. 13 - 13.50 through 13.54 Texts Sent and Received...Ch. 13 - 13.50 through 13.54 Texts Sent and Received...Ch. 13 - 13.50 through 13.54 Texts Sent and Received...Ch. 13 - Geometric Mean The dotplot shows the number of...Ch. 13 - Looking at the data about contacting mom (exercise...Ch. 13 - Resampling Moms We performed a randomization test...Ch. 13 - Prob. 58CRECh. 13 - Prob. 59CRECh. 13 - Prob. 60CRE
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How is a sample related to a population?
Elementary Statistics: Picturing the World (7th Edition)
Reading, Writing, and Rounding Whole Numbers Write in words. 357
Mathematics for the Trades: A Guided Approach (11th Edition) (What's New in Trade Math)
First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...
Calculus: Early Transcendentals (2nd Edition)
153. A rain gutter is made from sheets of aluminum that are 20 inches wide. As shown in the figure, the edges ...
College Algebra (7th Edition)
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
Find E(X) for each of the distributions given in Exercise 2.1-3.
Probability And Statistical Inference (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Harvard University California Institute of Technology Massachusetts Institute of Technology Stanford University Princeton University University of Cambridge University of Oxford University of California, Berkeley Imperial College London Yale University University of California, Los Angeles University of Chicago Johns Hopkins University Cornell University ETH Zurich University of Michigan University of Toronto Columbia University University of Pennsylvania Carnegie Mellon University University of Hong Kong University College London University of Washington Duke University Northwestern University University of Tokyo Georgia Institute of Technology Pohang University of Science and Technology University of California, Santa Barbara University of British Columbia University of North Carolina at Chapel Hill University of California, San Diego University of Illinois at Urbana-Champaign National University of Singapore McGill…arrow_forwardName Harvard University California Institute of Technology Massachusetts Institute of Technology Stanford University Princeton University University of Cambridge University of Oxford University of California, Berkeley Imperial College London Yale University University of California, Los Angeles University of Chicago Johns Hopkins University Cornell University ETH Zurich University of Michigan University of Toronto Columbia University University of Pennsylvania Carnegie Mellon University University of Hong Kong University College London University of Washington Duke University Northwestern University University of Tokyo Georgia Institute of Technology Pohang University of Science and Technology University of California, Santa Barbara University of British Columbia University of North Carolina at Chapel Hill University of California, San Diego University of Illinois at Urbana-Champaign National University of Singapore…arrow_forwardA company found that the daily sales revenue of its flagship product follows a normal distribution with a mean of $4500 and a standard deviation of $450. The company defines a "high-sales day" that is, any day with sales exceeding $4800. please provide a step by step on how to get the answers in excel Q: What percentage of days can the company expect to have "high-sales days" or sales greater than $4800? Q: What is the sales revenue threshold for the bottom 10% of days? (please note that 10% refers to the probability/area under bell curve towards the lower tail of bell curve) Provide answers in the yellow cellsarrow_forward
- Find the critical value for a left-tailed test using the F distribution with a 0.025, degrees of freedom in the numerator=12, and degrees of freedom in the denominator = 50. A portion of the table of critical values of the F-distribution is provided. Click the icon to view the partial table of critical values of the F-distribution. What is the critical value? (Round to two decimal places as needed.)arrow_forwardA retail store manager claims that the average daily sales of the store are $1,500. You aim to test whether the actual average daily sales differ significantly from this claimed value. You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. Showing the calculation is a must. If calculation is missing,so please provide a step by step on the answers Numerical answers in the yellow cellsarrow_forwardShow all workarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Sampling Methods and Bias with Surveys: Crash Course Statistics #10; Author: CrashCourse;https://www.youtube.com/watch?v=Rf-fIpB4D50;License: Standard YouTube License, CC-BY
Statistics: Sampling Methods; Author: Mathispower4u;https://www.youtube.com/watch?v=s6ApdTvgvOs;License: Standard YouTube License, CC-BY