
Concept explainers
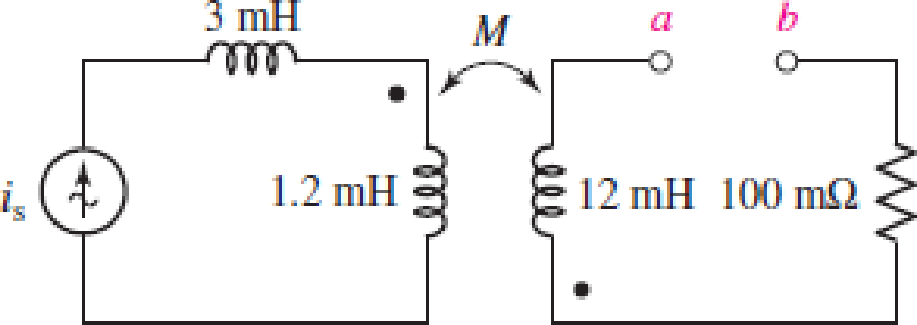
Consider the circuit represented in Fig. 13.53. The coupling coefficient k = 0.75. If is = 5 cos 200t mA, calculate the total energy stored at t = 0 and t = 5 ms if (a) a-b is open-circuited (as shown); (b) a-b is short-circuited.
FIGURE 13.53
(a)
Find the total energy stored in the system at
Answer to Problem 27E
The total energy stored in the system at
Explanation of Solution
Given data:
Refer to Figure 13.53 in the textbook for the given circuit.
The terminals a-b in the given circuit are open circuited.
Formula used:
Write the expression for energy stored in the magnetic field due to self-inductance of the coil at an instant of time as follows:
Here,
Calculation:
As the terminals a-b in the given circuit are open circuited, the current through the secondary winding loop is 0 A. Therefore, the total energy stored in the system is only due to the primary coils of the given circuit.
From the given circuit, find the value of inductance of primary coil when the terminals a-b in the given circuit are open circuited as follows:
Find the current through the primary coil at
Modify the expression in Equation (1) for energy stored in the system due to the coil
Substitute
Find the current through the primary coil at
Modify the expression in Equation (1) for energy stored in the system due to the coil
Substitute
Conclusion:
Thus, the total energy stored in the system at
(b)
Find the total energy stored in the system at
Answer to Problem 27E
The total energy stored in the system at
Explanation of Solution
Given data:
The terminals a-b in the given circuit are short-circuited.
Formula used:
Write the expression for energy stored in the magnetic field due to mutual inductance of the coils at an instant of time as follows:
Here,
Write the expression for mutual inductance in terms of self-inductance of primary and secondary coils as follows:
Here,
Calculation:
Substitute
From the given circuit, find the current
Substitute
Simplify the expression as follows:
Find the current through the secondary coil at
From Part (a), the energy stored in the system due to the coil
Modify the expression in Equation (1) for energy stored in the system due to the coil
Substitute
Rearrange the expression in Equation (2) to find the energy stored in the magnetic field due to the mutual inductance of the coils at
Substitute
Write the expression for total energy stored in the system at
Substitute
From Part (a), the energy stored in the system due to the coil
Find the current through the secondary coil at
Modify the expression in Equation (1) for energy stored in the system due to the coil
Substitute
Rearrange the expression in Equation (2) to find the energy stored in the magnetic field due to the mutual inductance of the coils at
Substitute
Modify the expression in Equation (4) for total energy stored in the system at
Substitute
Conclusion:
Thus, the total energy stored in the system at
Want to see more full solutions like this?
Chapter 13 Solutions
ENGINEERING CIRCUIT...(LL)>CUSTOM PKG.<
- Not use ai pleasearrow_forward49. For the circuit below, what is the best connection of the capacitor to filte voltage? ბი DO A O BO wwwww wwwww M m H E LOADarrow_forward5.25. Determine the corner frequency resulting from Cin in Fig. 5.47(d). For simplicity, assume C₁ is a short circuit. TVDD C₁ M2 RF Vin H w - Vout Cin M₁arrow_forward
- In the below circuit, find out the value of equivalent Thevenin's voltage and Thevenin's resistance at the terminal. 2000 0.25 A 400 2 800 2 0.1 Aarrow_forwardQ1: For the circuit shown in Figure-1, (a) Calculate the equivalent resistance of the circuit, RAB at the terminals A and B. [10] (b) When 50V dc source is switched at terminals A-B, solve for the voltage V₁ at the location shown. [10] 50V www 12Ω 10Ω 5Ω www www A + B 200 Figure-1 www 10Ω ww 25Ω 100arrow_forwarda. Write a PLC ladder diagram that allows the teacher to teach AND, OR, and XOR logic gates through using three PLC's digital input points and only one digital output point.arrow_forward
- rately by PRACTICE 4.2 For the circuit of Fig. 4.5, compute the voltage across each curren source. 202 ww 3A 30 ww 4Ω S 50 www Reference node FIGURE 4.5 Ans: V3A =5.235 V; 7A = 11.47 V. 7 Aarrow_forwardQ2) a) design and show me your steps to convert the following signal from continuous form to digital form: s(t)=3sin(3πt) -1 373 Colesarrow_forwardA sequence is defined by the relationship r[n] = [h[m]h[n+m]=hn*h-n where h[n] is a minimum-phase sequence and r[n]= 4 4 (u[n]+ 12" [n-1] 3 (a) Find R(z) and sketch the pole-zero diagram. (b) Determine the minimum-phase sequence h[n] to within a scale factor of ±1. Also, determine the z-transform H(z) of h[n].arrow_forward
- usıng j-k and D flipflop design a counter that counts 0,2,1 again as shown below ın the tablearrow_forwardfind the minterms of the followıng boolean expressıon desıgn F's cırcuit using one of the approciate decoders given below and a NOR gateF(A,B,C,D)=(A+'BC)(B 'C+'A 'D + CD)arrow_forward64) answer just two from three the following terms: A) Design ADC using the successive method if the Vmax=(3) volt, Vmin=(-2) volt, demonstrate the designing system for vin-1.2 volt. Successive Approximation ADC Input Voltage-1.1 V -4-3.5-3 -2.5 -2 -1.5 +1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 1 T -8 -7 -6 -5 -3 +2 -1 0 1 2 3 4 5 6 7 X=1??? 1st guess: -0.25 V (too high) X=11?? 2nd guess: -2.25 V (too low) 3rd guess: -1.25 V (too low) X=1110 X=111? 4th guess: -0.75 V (too high) Make successive guesses and use a comparator to tell whether your guess is too high or too low. Each guess determines one bit of the answer and cuts the number of remaining possibilities in half.arrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





