Linear Algebra With Applications (classic Version)

5th Edition

ISBN: 9780135162972

Author: BRETSCHER, OTTO

Publisher: Pearson Education, Inc.,

See similar textbooks

Videos

Textbook Question

Chapter 1.3, Problem 1E

GOAL Use the reduced row-echelon form of the augmented matrix to find the number of solutions of a linear system. Apply the definition of the rank of a matrix. Compute the product A x → in terms of the rows or the columns of A. Represent a linear system in vector or matrix form.

1. The reduced row-echelon forms of the augmented matrices of three systems are given here. How many solutions does each system have?

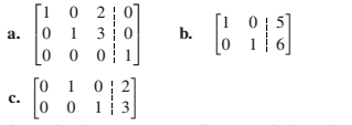
Chapter 1.3, Problem 1E, GOAL Use the reduced row-echelon form of the augmented matrix to find the number of solutions of a

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 1.2, Problem 80E

Chapter 1.3, Problem 2E

Students have asked these similar questions

1 Matching 10 points Factor and Solve 1)x3-216 0, x = {6,[B]} 2) 16x3 = 54 x-[3/2,[D]] 3)x4x2-42 0 x= [ +/-isqrt(7), [F] } 4)x+3-13-9x x=[+/-1.[H]] 5)x38x2+16x=0, x = {0,[K}} 6) 2x6-10x-48x2-0 x-[0, [M], +/-isqrt(3)) 7) 3x+2x²-8 x = {+/-i sqrt(2), {Q}} 8) 5x³-3x²+32x=2x+18 x = {3/5, [S]} [B] [D] [F] [H] [K] [M] [Q] +/-2 sqrt(2) +/- i sqrt(6) (-3+/-3 i sqrt(3))/4 +/- 1 +/-sqrt(6) +/- 2/3 sqrt(3) 4 -3 +/- 3 i sqrt(3) [S]

The only problems I need help with ae the last 8 ones, Thanks

Graph without using the calculator y-1 = | x+4 |

Chapter 1 Solutions

Linear Algebra With Applications (classic Version)

Ch. 1.1 - In Exercises 11 through 13,find all solutions of...Ch. 1.1 - In Exercises 11 through 13, find all solutions of...Ch. 1.1 - In Exercises 11 through 13, find all solutions of...Ch. 1.1 - In Exercises 14 through 16,find all solutions of...Ch. 1.1 - In Exercises 14 through 16, find all solutions of...Ch. 1.1 - In Exercises 14 through 16, find all solutions of...Ch. 1.1 - Find all solutions of the linear system | x+2y=a...Ch. 1.1 - Find all solutions of the linear system...Ch. 1.1 - Consider the linear system...Ch. 1.1 - Consider the linear system |x+yz=2x+2y+z=3x+y+( k...Ch. 1.1 - The sums of any two of three real numbers are 24,...Ch. 1.1 - Emile and Gertrude are brother and sister. Emile...Ch. 1.1 - Consider a two-commodity market. When the...Ch. 1.1 - The Russian-born U.S. economist and Nobel laureate...Ch. 1.1 - Find the outputs a andb needed to satisfy the...Ch. 1.1 - Consider the differential equation...Ch. 1.1 - Find all solutions of the system |7xy=x6x+8y=y| ,...Ch. 1.1 - On a sunny summer day, you are taking the...Ch. 1.1 - On your next trip to Switzerland, you should take...Ch. 1.1 - In a grid of wires, the temperature at exterior...Ch. 1.1 - Find the polynomial of degree 2 [a polynomial of...Ch. 1.1 - Find a polynomial of degree 2 [of the form...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find the function f(t) of the form f(t)=ae3t+be2t...Ch. 1.1 - Find the function f(t) of the form...Ch. 1.1 - Prob. 39E Ch. 1.1 - Find the ellipse centered at the origin that runs...Ch. 1.1 - Find all points (a,b,c) in space for which the...Ch. 1.1 - Linear systems are particularly easy to solve when...Ch. 1.1 - Consider the linear system |x+y=1x+ t 2y=t| ,...Ch. 1.1 - Find a system of linear equations with three...Ch. 1.1 - Find a system of linear equations with three...Ch. 1.1 - Boris and Marina are shopping for chocolate bars....Ch. 1.1 - Here is another method to solve a system of linear...Ch. 1.1 - A hermit eats only two kinds of food: brown rice...Ch. 1.1 - I have 32 bills in my wallet, in the denominations...Ch. 1.1 - Some parking meters in Milan, Italy, accept coins...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Prob. 16E Ch. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Determine which of the matrices below are in...Ch. 1.2 - Find all 41 matrices in reduced row-echelon form.Ch. 1.2 - For which values of a, b, c, d, and e is the...Ch. 1.2 - For which values of a, b, c, d, and e is the...Ch. 1.2 - We say that two nm matrices in reduced...Ch. 1.2 - How many types of 32 matrices in reduced...Ch. 1.2 - How many types of 23 matrices in reduced...Ch. 1.2 - Prob. 25E Ch. 1.2 - Suppose matrix A is transformed into matrix B...Ch. 1.2 - Prob. 27E Ch. 1.2 - Consider an nm in matrix A. Can you transform...Ch. 1.2 - Prob. 29E Ch. 1.2 - Suppose you subtract a multiple of an equation in...Ch. 1.2 - Balancing a chemical reaction. Consider the...Ch. 1.2 - Find the polynomial of degree 3 [a polynomial of...Ch. 1.2 - Find the polynomial of degree 4 whose graph...Ch. 1.2 - Cubic splines. Suppose you are in charge of the...Ch. 1.2 - Find the polynomial f(t) of degree 3 such that...Ch. 1.2 - The dot product of two vectors x=[ x 1 x 2 x n]...Ch. 1.2 - Find all vectors in 4 that are perpendicular to...Ch. 1.2 - Find all solutions x1,x2,x3 of the equation...Ch. 1.2 - Prob. 39E Ch. 1.2 - If we consider more than three industries in an...Ch. 1.2 - Consider the economy of Israel in 1958.11 The...Ch. 1.2 - Prob. 42E Ch. 1.2 - Prob. 43E Ch. 1.2 - The accompanying sketch represents a maze of...Ch. 1.2 - Let S(t) be the length of the tth day of the year...Ch. 1.2 - Prob. 46E Ch. 1.2 - Consider the equations...Ch. 1.2 - Consider the equations |y+2kz=0x+2y+6z=2kx+2z=1| ,...Ch. 1.2 - a. Find all solutions x1,x2,x3,x4 of the system...Ch. 1.2 - For an arbitrary positive integer n3 , find all...Ch. 1.2 - Prob. 51E Ch. 1.2 - Find all the polynomials f(t) of degree 3 such...Ch. 1.2 - Prob. 53E Ch. 1.2 - Prob. 54E Ch. 1.2 - Prob. 55E Ch. 1.2 - Prob. 56E Ch. 1.2 - Prob. 57E Ch. 1.2 - Prob. 58E Ch. 1.2 - Prob. 59E Ch. 1.2 - Prob. 60E Ch. 1.2 - Prob. 61E Ch. 1.2 - Prob. 62E Ch. 1.2 - Students are buying books for the new semester....Ch. 1.2 - Prob. 64E Ch. 1.2 - At the beginning of a political science class at a...Ch. 1.2 - Prob. 66E Ch. 1.2 - Prob. 67E Ch. 1.2 - Prob. 68E Ch. 1.2 - Prob. 69E Ch. 1.2 - Prob. 70E Ch. 1.2 - Prob. 71E Ch. 1.2 - Prob. 72E Ch. 1.2 - Pigeons are sold at the rate of 5 for 3 panas,...Ch. 1.2 - Prob. 74E Ch. 1.2 - Prob. 75E Ch. 1.2 - Prob. 76E Ch. 1.2 - Prob. 77E Ch. 1.2 - Prob. 78E Ch. 1.2 - Prob. 79E Ch. 1.2 - Prob. 80E Ch. 1.3 - GOAL Use the reduced row-echelon form of the...Ch. 1.3 - Find the rank of the matrices in Exercises 2...Ch. 1.3 - Find the rank of the matrices in Exercises 2...Ch. 1.3 - Find the rank of the matrices in Exercises 2...Ch. 1.3 - a. Write the system |x+2y=73x+y=11| in vector...Ch. 1.3 - Consider the vectors v1,v2,v3 in 2 (sketched in...Ch. 1.3 - Consider the vectors v1,v2,v3 in 2 shown in the...Ch. 1.3 - Consider the vectors v1,v2,v3,v4 in 2 shown in...Ch. 1.3 - Write the system |x+2y+3z=14x+5y+6z=47x+8y+9z=9|...Ch. 1.3 - Compute the dot products in Exercises 10 through...Ch. 1.3 - Compute the dot products in Exercises 10 through...Ch. 1.3 - Compute the dot products in Exercises 10 through...Ch. 1.3 - Compute the products Axin Exercises 13 through 15...Ch. 1.3 - Compute the products Axin Exercises 13 through 15...Ch. 1.3 - Compute the products Axin Exercises 13 through 15...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - a. Find [234567]+[753101] . b. Find 9[112345] .Ch. 1.3 - Use technology to compute the product...Ch. 1.3 - Consider a linear system of three equations with...Ch. 1.3 - Consider a linear system of four equations with...Ch. 1.3 - Let A be a 44 matrix, and let b and c be two...Ch. 1.3 - Let A be a 44 matrix, and let b and c be two...Ch. 1.3 - Let A be a 43 matrix, and let b and c be two...Ch. 1.3 - If the rank of a 44 matrix A is 4, what is...Ch. 1.3 - If the rank of a 53 matrix A is 3, what is...Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - Let A be the nn matrix with all 1‘s on the...Ch. 1.3 - We define the vectors e1=[001],e2=[010],e3=[001]...Ch. 1.3 - In m , we define ei=[0010]ithcomponent . If A is...Ch. 1.3 - Find a 33 matrix A such that...Ch. 1.3 - Find all vectors x such that Ax=b , where...Ch. 1.3 - Prob. 38E Ch. 1.3 - Prob. 39E Ch. 1.3 - Prob. 40E Ch. 1.3 - Prob. 41E Ch. 1.3 - Prob. 42E Ch. 1.3 - Prob. 43E Ch. 1.3 - Consider an nm matrix A with more rows than...Ch. 1.3 - Prob. 45E Ch. 1.3 - Prob. 46E Ch. 1.3 - A linear system of the form Ax=0 is called...Ch. 1.3 - Consider a solution x1 of the linear system Ax=b...Ch. 1.3 - Consider the accompanying table. For some linear...Ch. 1.3 - Consider a linear system Ax=b , where A is a 43...Ch. 1.3 - Consider an nm matrix A, an rs matrix B, and...Ch. 1.3 - Consider the matrices A=[1012] and B=[0110] .Can...Ch. 1.3 - If A and B are two nm matrices, is (A+B)x=Ax+Bx...Ch. 1.3 - Prob. 54E Ch. 1.3 - Prob. 55E Ch. 1.3 - Is the vector [301385662] a linear combination of...Ch. 1.3 - Prob. 57E Ch. 1.3 - For which values of the constants b and c is the...Ch. 1.3 - For which values of the constants c and d is...Ch. 1.3 - For which values of the constants a, b, c and d is...Ch. 1.3 - For which values of the constant c is [1cc2] a...Ch. 1.3 - For which values of the constant c is [1cc2] a...Ch. 1.3 - In Exercises 63 through 68, consider the vectors...Ch. 1.3 - In Exercises 63 through 68, consider the vectors...Ch. 1.3 - Prob. 65E Ch. 1.3 - Prob. 66E Ch. 1.3 - Prob. 67E Ch. 1.3 - Prob. 68E Ch. 1.3 - Prob. 69E Ch. 1.3 - Let A be the nn matrix with 0’s on the main...Ch. 1 - TRUE OR FALSE? 19 Determine whether the statements...Ch. 1 - TRUE OR FALSE? 19 Determine whether the statements...Ch. 1 - Matrix [120001000] is in reduced row-echelon form.Ch. 1 - A system of four linear equations in three...Ch. 1 - There exists a 34 matrix with rank 4.Ch. 1 - If A is a 34 matrix and vector v is in 4 , then...Ch. 1 - If the 44 matrix A has rank 4, then any linear...Ch. 1 - There exists a system of three linear equations...Ch. 1 - There exists a 55 matrix A of rank 4 such that the...Ch. 1 - If matrix A is in reduced row-echelon form, then...Ch. 1 - The system [123456000]x=[123] is inconsistent.Ch. 1 - There exists 22 matrix A such that A=[12]=[34] .Ch. 1 - If A is a nonzero matrix of the form [abba] , then...Ch. 1 - rank [111123136]=3 Ch. 1 - The system Ax=[0001] is inconsistent for all 43...Ch. 1 - There exists a 22 matrix A such that A=[11]=[12]...Ch. 1 - rank [222222222]=2 Ch. 1 - [111315171921][131]=[131921]Ch. 1 - There exists a matrix A such that A=[12]=[357] .Ch. 1 - Vector [123] is a linear combination of vectors...Ch. 1 - If the system Ax=b has a unique solution, then...Ch. 1 - If A is any 43 matrix, then there exists a vector...Ch. 1 - There exist scalars a and b such that matrix...Ch. 1 - If v and w are vectors in 4 , then v must be a...Ch. 1 - If u,v , and w are nonzero vectors in 2 , then w...Ch. 1 - If v and w are vectors in 4 , then the zero vector...Ch. 1 - If A and B are any two 33 matrices of rank2,then...Ch. 1 - If vector u is a linear combination of vectors v...Ch. 1 - A linear system with fewer unknowns than...Ch. 1 - The rank of any upper triangular matrix is the...Ch. 1 - There exists a 43 matrix A of rank 3 such that...Ch. 1 - The system Ax=b is inconsistent if (and only...Ch. 1 - If A is a 43 matrix of rank 3 and Au=Aw for two...Ch. 1 - If A is a 44 matrix and the system Ax=[2345] has...Ch. 1 - If vector u is a linear combination of vectors v...Ch. 1 - If A=[uvw] and rref(A)=[002013000] , then the...Ch. 1 - If A and B are matrices of the same size, then the...Ch. 1 - If A and B are any two nn matrices of rank n, then...Ch. 1 - If a vector v in 4 is a linear combination of u...Ch. 1 - If matrix E is in reduced row-echelon form, and if...Ch. 1 - The linear system Ax=b consistent if (and only if)...Ch. 1 - If A is a 34 matrix of rank 3, then the system...Ch. 1 - If two matrices A and B have the same reduced...Ch. 1 - If matrix E is in reduced row-echelon form, and if...Ch. 1 - If A and B are two 22 matrices such that the...Ch. 1 - A lower triangular 33 matrix has rank 3 if (and...Ch. 1 - If adbc0 , then the matrix [abcd] must have rank...Ch. 1 - If vector w is a linear combination of u and v ,...Ch. 1 - If the linear system Ax=b has a unique solution...Ch. 1 - A matrix is called a 0-1-matrix if all of its...

Additional Math Textbook Solutions

Find more solutions based on key concepts

Testing Hypotheses. In Exercises 13-24, assume that a simple random sample has been selected and test the given...

Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)

Evaluate the integrals in Exercises 1–46. 1.

University Calculus: Early Transcendentals (4th Edition)

The largest polynomial that divides evenly into a list of polynomials is called the _______.

Elementary & Intermediate Algebra

Length of a Guy Wire A communications tower is located at the top of a steep hill, as shown. The angle of incli...

Precalculus: Mathematics for Calculus (Standalone Book)

23. A plant nursery sells two sizes of oak trees to landscapers. Large trees cost the nursery $120 from the gro...

College Algebra (Collegiate Math)

True or False The quotient of two polynomial expressions is a rational expression, (p. A35)

Precalculus

Knowledge Booster

$Algebra$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.