Chapter 13, Problem 13.22P

To determine

(a)

The expression for $\frac{X_1\left(j\omega \right)}{F\left(j\omega \right)}$.

The expression for $\frac{X_2\left(j\omega \right)}{F\left(j\omega \right)}$.

Answer to Problem 13.22P

The expression for $\frac{X_1\left(j\omega \right)}{F\left(j\omega \right)}$ is $\frac{\sqrt{4{\varsigma }^2+{\mu }^2{r}^2}}{\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}$.

The expression for $\frac{X_2\left(j\omega \right)}{F\left(j\omega \right)}$ is $\frac{2\varsigma }{{\omega }_1^2\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}$.

Explanation of Solution

Given information:

The main mass is $m_1$.

Write the expression for force of mass 1.

$\begin{array}{l}f=m_1{\ddot{x}}_1+c\left({\dot{x}}_1-{\dot{x}}_2\right)+\frac{k}{2}{x}_1+\frac{k}{2}{x}_1\\ m_1{\ddot{x}}_1=f-c\left({\dot{x}}_1-{\dot{x}}_2\right)-k{x}_1\end{array}$..... (I)

Here, mass of body 1 is $m_1$, damping coefficient is $c$, velocity of mass 1 is ${\dot{x}}_1$, velocity of mass 2 is ${\dot{x}}_2$, stiffness is $k$, displacement is $x$, acceleration of mass 1 is ${\ddot{x}}_1$ and the coefficient of friction is $f$.

Write the expression for absorber mass.

$m_2{\ddot{x}}_2=-c{\dot{x}}_2+c{\dot{x}}_1$..... (II)

Here, mass of the absorber is $m_2$. and the acceleration of absorber is ${\ddot{x}}_2$.

Take Laplace transform of Equation (I).

$\begin{array}{l}L\left(m_1{\ddot{x}}_1\right)=L\left(f\right)-L\left[c\left({\dot{x}}_1-{\dot{x}}_2\right)\right]-L\left[k{x}_1\right]\\ m_1{s}^2{X}_1\left(s\right)+cs{X}_1\left(s\right)-cs{X}_2\left(s\right)+k{X}_1\left(s\right)=F\left(s\right)\\ \left(m_1{s}^2+cs+k\right)X_1\left(s\right)-cs{X}_2\left(s\right)=F\left(s\right)\end{array}$..... (III)

Take Laplace transform of Equation (II).

$\begin{array}{l}L\left[m_2{\ddot{x}}_2\right]=-L\left[c{\dot{x}}_2\right]+L\left[c{\dot{x}}_1\right]\\ m_2{s}^2{X}_2\left(s\right)=-cs{X}_2\left(s\right)+cs{X}_1\left(s\right)\\ -cs{X}_1\left(s\right)+\left(m_2{s}^2+cs\right)X_2\left(s\right)=0\end{array}$..... (IV)

Apply Cramer rule in Equation (III) and (IV).

$\left(\begin{array}{cc}{m}_1{s}^2+cs+k& -cs\\ -cs& m_2{s}^2+cs\end{array}\right)\left(\begin{array}{l}{X}_1\left(s\right)\\ X_2\left(s\right)\end{array}\right)=\left(\begin{array}{l}F\left(s\right)\\ 0\end{array}\right)$..... (V)

Further soving Equation (V).

$\begin{array}{l}D\left(s\right)=m_1{m}_2{s}^4+c{m}_2{s}^3+k{m}_2{s}^2+m_{1}c{s}^3+{\left(cs\right)}^2+cks-c{s}^2\\ D\left(s\right)=s\left(m_1{m}_2{s}^3+c\left(m_2+m_1\right)s^2+k{m}_{2}s+m_{1}c{s}^3+ck\right)\end{array}$..... (VI)

Write the expression for parameter $\mu$.

$\mu =\frac{m_1}{m_2}$..... (VII)

Write the expression for parameter ${\omega }_1^2$.

${\omega }_1^2=\frac{k}{m_1}$..... (VIII)

Write the expression for parameter $\varsigma$.

$\varsigma =\frac{c}{2\sqrt{m_{1}k}}$..... (IX)

Write the expression for parameter $r$.

$r=\frac{\omega }{{\omega }_1}$..... (X)

Here, angular speed of main mass is ${\omega }_1$.

Substitute $j\omega$ for $s$ in Equation (VI).

$\begin{array}{l}D\left(j\omega \right)=s\left(m_1{m}_2{\left(j\omega \right)}^3+c\left(m_2+m_1\right){\left(j\omega \right)}^2+k{m}_2\left(j\omega \right)+m_{1}c{\left(j\omega \right)}^3+ck\right)\\ D\left(j\omega \right)=|j\omega \left[\left(-m_1{m}_2{\omega }^{3}j-c\left(m_2+m_1\right){\omega }^2+k{m}_2\omega j+ck\right)\right]\end{array}$..... (XI)

Substitute $\frac{k}{m_1}$ for ${\omega }_1^2$, $\varsigma$ for $\frac{c}{2\sqrt{m_{1}k}}$, $r$ for $\frac{\omega }{{\omega }_1}$ and $\mu$ for $\frac{m_1}{m_2}$ in Equation (XI).

$\begin{array}{c}D\left(j\omega \right)=\left|j\omega \left[\begin{array}{l}-m_1\left(\mu m_1\right){\left(r{\omega }_1\right)}^{3}j-\left(2\varsigma \sqrt{m_1}k\right)\left(m_1\mu m_1\right){\left(r{\omega }_1\right)}^2+\\ \left({\omega }_1^2{m}_1\right)\left(\mu m_1\right)\left(r{\omega }_1\right)j+\left(2\varsigma \sqrt{m_1}k\right)\left({\omega }_1^2{m}_1\right)\end{array}\right]\right|\\ =m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}\end{array}$..... (XII)

Apply Cramer rule in Equation (V) to obtain $D_1\left(s\right)$.

$\begin{array}{l}\left(\begin{array}{cc}{m}_1{s}^2+cs+k& -cs\\ -cs& m_2{s}^2+cs\end{array}\right)\left(\begin{array}{l}{X}_1\left(s\right)\\ X_2\left(s\right)\end{array}\right)=\left(\begin{array}{l}F\left(s\right)\\ 0\end{array}\right)\\ D_1\left(s\right)=F\left(s\right)\times \left(m_2{s}^2+cs\right)-\left(0\times cs\right)\\ D_1\left(s\right)=F\left(s\right)\left(m_2{s}^2+cs\right)\end{array}$..... (XIII)

Apply Cramer rule in Equation (V) to obtain $D_2\left(s\right)$.

$\begin{array}{l}\left(\begin{array}{cc}{m}_1{s}^2+cs+k& F\left(s\right)\\ -cs& 0\end{array}\right)=0\\ D_2\left(s\right)=-\left(-cs\right)\times F\left(s\right)\\ D_2\left(s\right)=csF\left(s\right)\end{array}$..... (XIV)

Write the expression for $X_1\left(s\right)$.

$X_1\left(s\right)=\frac{D_1\left(s\right)}{D\left(s\right)}$..... (XV)

Substitute $F\left(s\right)\left(m_2{s}^2+cs\right)$ for $D_1\left(s\right)$ and $m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}$ for $D\left(s\right)$ in Equation (XIV).

$\begin{array}{l}{X}_1\left(s\right)=\frac{F\left(s\right)\left(m_2{s}^2+cs\right)}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\\ \frac{X_1\left(s\right)}{F\left(s\right)}=\frac{\left(m_2{s}^2+cs\right)}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\end{array}$..... (XV)

Substitute $j\omega$ for $s$ in Equation (XV).

$\begin{array}{c}\frac{X_1\left(j\omega \right)}{F\left(j\omega \right)}=\frac{\left(m_2{\left(j\omega \right)}^2+c\left(j\omega \right)\right)}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\\ =\frac{-m_2{\omega }^2+c\omega j}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\end{array}$..... (XVI)

Simplify Equation (XVI) by substituting $\frac{k}{m_1}$ for ${\omega }_1^2$, $\varsigma$ for $\frac{c}{2\sqrt{m_{1}k}}$, $r$ for $\frac{\omega }{{\omega }_1}$ in Equation (XVI).

$\begin{array}{c}\frac{X_1\left(j\omega \right)}{F\left(j\omega \right)}=\frac{-m_2{\omega }^2+c\omega j}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\\ =m_{1}r{\omega }_1^4\sqrt{4{\varsigma }^2+{\mu }^2{r}^2}\end{array}$

Substitute $m_{1}r{\omega }_1^4\sqrt{4{\varsigma }^2+{\mu }^2{r}^2}$ for $-m_2{\omega }^2+c\omega j$ in Equation (XVI).

$\begin{array}{l}\frac{X_1\left(j\omega \right)}{F\left(j\omega \right)}=\frac{-m_2{\omega }^2+c\omega j}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\\ \frac{X_1\left(j\omega \right)}{F\left(j\omega \right)}=\frac{\sqrt{4{\varsigma }^2+{\mu }^2{r}^2}}{m_1{\omega }_1^2\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\\ \frac{k{X}_1\left(j\omega \right)}{F\left(j\omega \right)}=\frac{k\sqrt{4{\varsigma }^2+{\mu }^2{r}^2}}{m_1{\omega }_1^2\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\end{array}$..... (XVII)

Write the expression for stiffness.

$k=m_1{\omega }_1^2$..... (XVIII)

Substitute $m_1{\omega }_1^2$ for $k$ in Equation (XVII).

$\begin{array}{l}\frac{k{X}_1\left(j\omega \right)}{F\left(j\omega \right)}=\frac{m_1{\omega }_1^2\sqrt{4{\varsigma }^2+{\mu }^2{r}^2}}{m_1{\omega }_1^2\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\\ \frac{k{X}_1\left(j\omega \right)}{F\left(j\omega \right)}=\frac{\sqrt{4{\varsigma }^2+{\mu }^2{r}^2}}{\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\end{array}$..... (XIX)

Write the expression for $X_2\left(s\right)$.

$X_2\left(s\right)=\frac{D_2\left(s\right)}{D\left(s\right)}$..... (XX)

Substitute $csF\left(s\right)$ for $D_2\left(s\right)$ and $m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}$ for $D\left(s\right)$ in equation (XX).

$\begin{array}{l}{X}_2\left(s\right)=\frac{csF\left(s\right)}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\\ \frac{X_2\left(s\right)}{F\left(s\right)}=\frac{cs}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\end{array}$..... (XXI)

Substitute $j\omega$ for $s$ in Equation (XXI).

$\frac{X_2\left(j\omega \right)}{F\left(j\omega \right)}=\frac{c\left(j\omega \right)}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}$..... (XXII)

Simplify Equation (XXII).

$\begin{array}{l}\frac{X_2\left(j\omega \right)}{F\left(j\omega \right)}=\left|\frac{c\left(j\omega \right)}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\right|\\ \frac{X_2\left(j\omega \right)}{F\left(j\omega \right)}=\frac{2\varsigma m_1^2{\omega }_1^{2}r}{m_1{\omega }_1^{4}r\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\\ \frac{X_2\left(j\omega \right)}{F\left(j\omega \right)}=\frac{2\varsigma }{{\omega }_1^2\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}\end{array}$.

Conclusion:

The expression for $\frac{X_1\left(j\omega \right)}{F\left(j\omega \right)}$ is $\frac{\sqrt{4{\varsigma }^2+{\mu }^2{r}^2}}{\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}$.

The expression for $\frac{X_2\left(j\omega \right)}{F\left(j\omega \right)}$ is $\frac{2\varsigma }{{\omega }_1^2\sqrt{{\left(2\varsigma \right)}^2\left[{\left(1-\left(1+\mu \right)r^2\right)}^2+{\mu }^2{r}^2{\left(1-r^2\right)}^2\right]}}$.

To determine

(b)

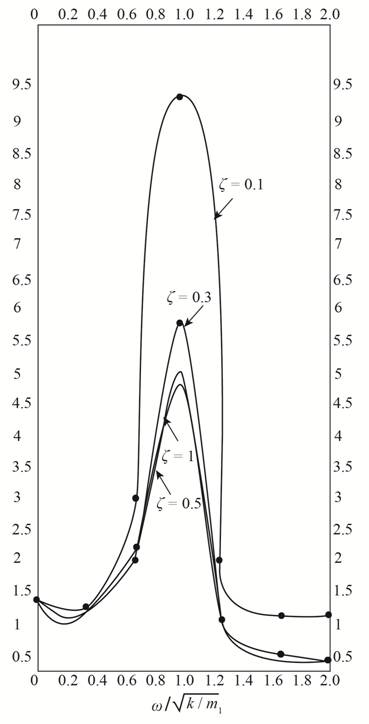
The plot between $\frac{k{X}_1}{F}$ and $\frac{\omega }{\sqrt{\frac{k}{m_1}}}$.

Answer to Problem 13.22P

The plot between $\frac{k{X}_1}{F}$ and $\frac{\omega }{\sqrt{\frac{k}{m_1}}}$ is shown in Figure-(1).

Explanation of Solution

Given information:

The main mass is $m_1$ and the absorber mass is $m_2$.

To plot the graph, consider some constant values such as $10$ for $m_1$, $30$ for $m_2$, ${10}^4$ for $k$ and $\left[0,2\right]$ for $r$.

Calculation:

Substitute $10$ for $m_1$ and $30$ for $m_2$ in equation (VII).

$\begin{array}{c}\mu =\frac{10}{30}\\ =0.3333\end{array}$

Substitute ${10}^4$ for $k$ and $10$ for $m_1$ in Equation (VIII).

$\begin{array}{l}{\omega }_1^2=\frac{{10}^4}{10}\\ {\omega }_1^2=1000\\ {\omega }_1=\sqrt{1000}\\ {\omega }_1=31.6\end{array}$

Assume $0$ for $\omega$ and $0.1$ for $\varsigma$.

Substitute $0$ for $\omega$ and $31.6$ for ${\omega }_1$ in Equation (X).

$\begin{array}{c}r=\frac{0}{31.6}\\ =0\end{array}$

Substitute $0$ for $r$, $0.3333$ for $\mu$ and $0.1$ for $\varsigma$ in Equation (XVIII).

$\begin{array}{c}\frac{k{X}_1\left(j\omega \right)}{F\left(j\omega \right)}=\frac{\sqrt{4{\left(0.1\right)}^2+{\left(0.3333\right)}^2{\left(0\right)}^2}}{\sqrt{{\left(2\left(0.1\right)\right)}^2\left[{\left(1-\left(1+0.3333\right){\left(0\right)}^2\right)}^2+{\left(0.3333\right)}^2{\left(0\right)}^2{\left(1-{\left(0\right)}^2\right)}^2\right]}}\\ =\frac{0.2}{0.141421}\\ =1.414\end{array}$

Calculate $\frac{\omega }{\sqrt{\frac{k}{m_1}}}$

Substitute $0$ for $\omega$ and ${10}^4$ for $k$ and $10$ for $m_1$ in $\frac{\omega }{\sqrt{\frac{k}{m_1}}}$.

$\frac{0}{\sqrt{\frac{{10}^4}{10}}}=0$

Prepare a table for various values of parameters.

$\omega$	$\varsigma$	$\frac{k{X}_1\left(j\omega \right)}{F\left(j\omega \right)}$	$\frac{\omega }{\sqrt{\frac{k}{m_1}}}$
$0$	$0.1$	$1.414$	$0$
$10$	$0.1$	$1.29$	$0.316$
$20$	$0.1$	$3.01$	$0.632$
$30$	$0.1$	$9.35$	$0.948$
$0$	$0.3$	$1.414$	$0$
$10$	$0.3$	$1.16$	$0.316$
$20$	$0.3$	$2.2$	$0.632$
$30$	$0.3$	$5.58$	$0.948$
$0$	$0.5$	$1.414$	$0$
$10$	$0.5$	$1.15$	$0.316$
$20$	$0.5$	$2.13$	$0.632$
$30$	$0.5$	$4.74$	$0.948$
$0$	$1$	$1.414$	$0$
$10$	$1$	$1.14$	$0.316$
$20$	$1$	$2.08$	$0.632$
$30$	$1$	$5.05$	$0.948$

The plot between $\frac{k{X}_1}{F}$ and $\frac{\omega }{\sqrt{\frac{k}{m_1}}}$ is shown below.

Figure-(1)

Conclusion:

The plot between $\frac{k{X}_1}{F}$ and $\frac{\omega }{\sqrt{\frac{k}{m_1}}}$ is shown below.