
(a)
Interpretation:
The rate constant for the growth in the number of transistor on an integrated circuit has to be determined using the given plot ln N versus year.
Concept introduction:
Rate of the reaction is the change in the concentration of reactant or a product with time.
The rate law expresses the relationship of the
Rate equation for the general reaction A+B → Product is,
Rate = k rate constat [A] [B]
Order of a reaction: The sum of exponents of the concentrations in the rate law for the reaction is said to be order of a reaction.
For first order reaction, −kt = ln ([A][A0])
[A] is the concentration of reactant A at time t [A]0 is the initial concentration of reactant, k is the rate constant.
Moore’s law states that the number of transistors per square inch on integrated circuits had doubled every year since their invention (1958).
(a)
Explanation of Solution
Given plot of ln N versus t (year) is shown below,
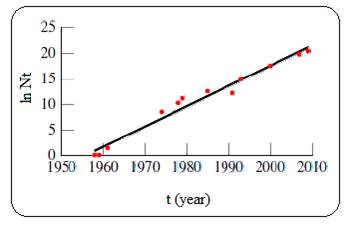
Figure 1
The plot of ln N versus t is linear for a process which follows first order kinetics. And so the given process follows first order kinetics.
The rate can be described using the equation,
Rate = ΔNtΔt = k Nt
Where N is the number of transistor on an integrated circuit, which is roughly doubles every 1.5 year according to the Moore’s law.
For first order reaction, −kt = ln ([A][A0])
[A] is the concentration of reactant A at time t [A]0 is the initial concentration of reactant, k is the rate constant.
For this case, the equation can be rearranged as follows,
ln Nt = kt + ln N0
Comparing this equation to the straight line equation (y = mx+c) thus, the slope of the line will give rate constant and it is 0.40 year −1
slope (m) = ΔyΔx = 14-101990-1980 = 410 = 0.40 year-1
(b)
Interpretation:
The time required for Nt to double has to be determined using the rate constant value.
Concept introduction:
The rate law expresses the relationship of the rate of a reaction to the rate constant.
Rate equation for the general reaction A+B → Product is,
Rate = k rate constat [A] [B]
Order of a reaction: The sum of exponents of the concentrations in the rate law for the reaction is said to be order of a reaction.
For first order reaction, −kt = ln ([A][A0])
[A] is the concentration of reactant A at time t [A]0 is the initial concentration of reactant, k is the rate constant.
Moore’s law states that the number of transistors per square inch on integrated circuits had doubled every year since their invention (1958).
(b)
Explanation of Solution
Given plot of ln N versus t (year) is shown below,

Figure 1
The time required for Nt to double can be determined as follows,
For first order reaction, −kt = ln ([A][A0])
[A] is the concentration of reactant A at time t [A]0 is the initial concentration of reactant, k is the rate constant.
k = 0.40 year −1
ln 2NtNt = (0.40 year -1) tln 2 = (0.40 year -1) × t0.693 = (0.40 year -1) × tt = 1.7 years
This value is very close to the value mentioned in Moore’s law.
(c)
Interpretation:
The number of transistors on an integrated circuit Nt in the year of 2100 has to be determined with respect to the Moore’s law.
Concept introduction:
The rate law expresses the relationship of the rate of a reaction to the rate constant.
Rate equation for the general reaction A+B → Product is,
Rate = k rate constat [A] [B]
Order of a reaction: The sum of exponents of the concentrations in the rate law for the reaction is said to be order of a reaction.
For first order reaction, −kt = ln ([A][A0])
[A] is the concentration of reactant A at time t [A]0 is the initial concentration of reactant, k is the rate constant.
Moore’s law states that the number of transistors per square inch on integrated circuits had doubled every year since their invention (1958).
(c)
Explanation of Solution
Given plot of ln N versus t (year) is shown below,

Figure 1
The time required for Nt to double can be determined as follows,
For first order reaction, −kt = ln ([A][A0])
For this case, the equation can be rearranged as follows,
ln Nt = kt + ln N0
Assume the year 1960 as t = 0 and taking ln N0 = 2
The year 2100 would corresponds to t = 2100 -1960 = 140 years
Substituting known values in the above mentioned equation,
ln Nt = (0.40 year -1) (140 year) + ln 2ln Nt = 56.69Nt = e(56.69)Nt = 4×1024
Thus, there will be 4×1024 transistors on a circuit in the year 2100. This number is unrealistic. In reality, many scientists believes that we are already approaching the end of Moore’s law due to quantum mechanical limits to the number of transistors that can be placed on a single circuit.
Want to see more full solutions like this?
Chapter 13 Solutions
CHEMISTRY 1111 LAB MANUAL >C<
- Another standard reference electrode is the standard calomel electrode: Hg2Cl2(s) (calomel) + 2e2 Hg() +2 Cl(aq) This electrode is usually constructed with saturated KCI to keep the Cl- concentration constant (similar to what we discussed with the Ag-AgCl electrode). Under these conditions the potential of this half-cell is 0.241 V. A measurement was taken by dipping a Cu wire and a saturated calomel electrode into a CuSO4 solution: saturated calomel electrode potentiometer copper wire CuSO4 a) Write the half reaction for the Cu electrode. b) Write the Nernst equation for the Cu electrode, which will include [Cu2+] c) If the voltage on the potentiometer reads 0.068 V, solve for [Cu²+].arrow_forward2. (Part B). Identify a sequence of FGI that prepares the Synthesis Target 2,4-dimethoxy- pentane. All carbons in the Synthesis Target must start as carbons in either ethyne, propyne or methanol. Hint: use your analysis of Product carbons' origins (Part A) to identify possible structure(s) of a precursor that can be converted to the Synthesis Target using one FGI. All carbons in the Synthesis Target must start as carbons in one of the three compounds below. H = -H H = -Me ethyne propyne Synthesis Target 2,4-dimethoxypentane MeOH methanol OMe OMe MeO. OMe C₂H₁₂O₂ Product carbons' origins Draw a box around product C's that came from A1. Draw a dashed box around product C's that came from B1.arrow_forwardDraw the skeletal ("line") structure of the smallest organic molecule that produces potassium 3-hydroxypropanoate when reacted with KOH. Click and drag to start drawing a structure. Sarrow_forward
- draw skeletal structures for the minor products of the reaction.arrow_forward1. Provide missing starting materials, reagents, products. If a product cannot be made, write NP (not possible) in the starting material box. C7H12O Ph HO H 1) 03-78 C 2) Me₂S + Ph .H OH + 2nd stereoisomer OH Ph D + enantiomer cat OsO 4 NMO H2O acetonearrow_forwardPlease note that it is correct and explains it rightly:Indicate the correct option. The proportion of O, C and H in the graphite oxide is:a) Constant, for the quantities of functional groups of acids, phenols, epoxy, etc. its constants.b) Depending on the preparation method, as much oxidant as the graphite is destroyed and it has less oxygen.c) Depends on the structure of the graphic being processed, whether it can be more tridimensional or with larger crystals, or with smaller crystals and with more edges.arrow_forward
- Check the box under each a amino acid. If there are no a amino acids at all, check the "none of them" box under the table. Note for advanced students: don't assume every amino acid shown must be found in nature. ནང་་་ OH HO HO NH2 + NH3 O OIL H-C-CO CH3-CH O C=O COOH COOH + H2N C-H O H2N C H CH3-CH CH2 HO H3N O none of them 口 CH3 CH2 OH Хarrow_forwardWhat is the systematic name of the product P of this chemical reaction? 010 HO-CH2-CH2-C-OH ☐ + NaOH P+ H2Oarrow_forward1. Provide missing starting materials, reagents, products. If a product cannot be made, write NP (not possible) in the starting material box. a) C10H12 Ph OMe AcOHg+ + enantiomer Br C6H10O2 + enantiomerarrow_forward
 General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning Living By Chemistry: First Edition TextbookChemistryISBN:9781559539418Author:Angelica StacyPublisher:MAC HIGHER
Living By Chemistry: First Edition TextbookChemistryISBN:9781559539418Author:Angelica StacyPublisher:MAC HIGHER Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning





