Precalculus
9th Edition
ISBN: 9780321716835
Author: Michael Sullivan
Publisher: Addison Wesley
expand_more
expand_more
format_list_bulleted
Question
Chapter 13, Problem 12CR
To determine
To calculate: The dimensions of a triangle and find its area where the triangle is
Expert Solution & Answer
Answer to Problem 12CR
Solution:
The sides of a triangle are a≈6.09,b=5,c=9, and angles are A=40∘,B≈31.9∘,C≈108.1∘, and area is approximately 14.46 square units.
Explanation of Solution
Given information:
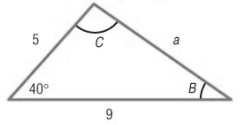
The triangle:
Formula used:
Law of cosine:
a2=b2+c2−2bccosA, where a,b,c are sides of a triangle, and the angles opposite to the sides a,b,c are A,B,C respectively.
Area of triangle =12×base×height
Calculation:
Here, from the triangle, b=5,c=9, and A=40∘.
By using law of cosine,
⇒a2=52+92−2(5)(9)cos40∘
⇒a2=106−90⋅(0.7660444431)
⇒a2=106−68.94399988
⇒a2=37.05600012
⇒a=±6.087363971≈±6.09
As the length of the side is never negative, so a≈6.09.
Now, to find angle B,
By using law of cosine,
⇒b2=a2+c2−2accosB∘
⇒52=(6.09)2+92−2(6.09)(9)cosB∘
⇒25−81−37.0881=−2(6.09)(9)cosB∘
⇒−93.0881=−109.62cosB∘
⇒cosB∘=93.0881109.62
⇒cosB∘=93.0881109.62
⇒cosB∘=0.8491890166
⇒B∘=cos−1(0.8491890166)
⇒B∘=31.87642838≈31.90
⇒B∘≈31.90
Now, to find angle C,
The sum of the angles of the triangle must be equal to 180∘.
A+B+C=180
Substitute A=40∘ and B≈31.90, it gives
⇒40+31.9+C=180
⇒C=180−71.9
⇒C=108.1∘
Therefore, the sides of a triangle are a≈6.09,b=5,c=9, and angles are A=40∘,B≈31.9∘,C≈108.1∘.
Now, to find area of a triangle, The base of the triangle =9
Need to find height of the triangle, say h,
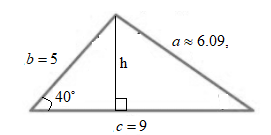
Using sine ratio to find h gives sin40∘=h5
⇒h=5sin40∘
By using the formula for area of a triangle, Area =12×9×5 sin40∘
=14.46272122≈14.46 square units.
Thus, area of a triangle is approximately 14.46 square units.
Therefore, the sides of a triangle are a≈6.09,b=5,c=9, and angles are A=40∘,B≈31.9∘,C≈108.1∘, and area is approximately 14.46 square units.
Chapter 13 Solutions
Precalculus
Ch. 13.1 - Prob. 1AYUCh. 13.1 - Prob. 2AYUCh. 13.1 - True or false The intersection of two sets is...Ch. 13.1 - Prob. 4AYUCh. 13.1 - Prob. 5AYUCh. 13.1 - Prob. 6AYUCh. 13.1 - Prob. 7AYUCh. 13.1 - Prob. 8AYUCh. 13.1 - Prob. 9AYUCh. 13.1 - Prob. 10AYU
Ch. 13.1 - If n( A )=15 , n( B )=20 , and n( AB )=10 , find...Ch. 13.1 - If n( A )=30 , n( B )=40 , and n( AB )=45 , find...Ch. 13.1 - If n( AB )=50 , n( AB )=10 , and n( B )=20 , find...Ch. 13.1 - If n( AB )=60 , n( AB )=40 , and n( A )=n( B ) ,...Ch. 13.1 - In Problems 15-22, use ihe information given in...Ch. 13.1 - In Problems 15-22, use ihe information given in...Ch. 13.1 - In Problems 15-22, use ihe information given in...Ch. 13.1 - In Problems 15-22, use ihe information given in...Ch. 13.1 - In Problems 15-22, use ihe information given in...Ch. 13.1 - In Problems 15-22, use ihe information given in...Ch. 13.1 - In Problems 15-22, use ihe information given in...Ch. 13.1 - In Problems 15-22, use ihe information given in...Ch. 13.1 - A man has shirts and ties. How many different...Ch. 13.1 - Blouses and Skirts A woman has 5 blouses and 8...Ch. 13.1 - Four-digit Numbers How many four-digit numbers can...Ch. 13.1 - Five-digit Numbers How many five-digit numbers can...Ch. 13.1 - Analyzing Survey Data In a consumer survey of ...Ch. 13.1 - Analyzing Survey Data In a student survey, 200...Ch. 13.1 - Analyzing Survey Data In a survey of 100 investors...Ch. 13.1 - Classifying Blood Types Human blood is classified...Ch. 13.1 - Demographics The following data represent the...Ch. 13.1 - Demographics The following data represent the...Ch. 13.1 - Stock Portfolios As a financial planner, you are...Ch. 13.1 - Prob. 34AYUCh. 13.2 - 0!= ; 1!= . (p. 642)Ch. 13.2 - Prob. 2AYUCh. 13.2 - A(n) __________ is an ordered arrangement of r...Ch. 13.2 - A(n) ___________ is an arrangement of r objects...Ch. 13.2 - P( n,r )= __________________.Ch. 13.2 - C( n,r )= _______________________.Ch. 13.2 - In Problems 7-14, find the value of each...Ch. 13.2 - In Problems 7-14, find the value of each...Ch. 13.2 - In Problems 7-14, find the value of each...Ch. 13.2 - In Problems 7-14, find the value of each...Ch. 13.2 - In Problems 7-14, find the value of each...Ch. 13.2 - In Problems 7-14, find the value of each...Ch. 13.2 - In Problems 7-14, find the value of each...Ch. 13.2 - In Problems 7-14, find the value of each...Ch. 13.2 - In Problems 15-22, use formula (2) to find the...Ch. 13.2 - In Problems 15-22, use formula (2) to find the...Ch. 13.2 - In Problems 15-22, use formula (2) to find the...Ch. 13.2 - In Problems 15-22, use formula (2) to find the...Ch. 13.2 - In Problems 15-22, use formula (2) to find the...Ch. 13.2 - In Problems 15-22, use formula (2) to find the...Ch. 13.2 - In Problems 15-22, use formula (2) to find the...Ch. 13.2 - In Problems 15-22, use formula (2) to find the...Ch. 13.2 - List all the ordered arrangements of 5 objects a ,...Ch. 13.2 - List all the ordered arrangements of 5 objects a ,...Ch. 13.2 - List all the ordered arrangements of 4 objects 1,...Ch. 13.2 - List all the ordered arrangements of 6 objects 1,...Ch. 13.2 - List all the combinations of 5 objects a , b , c ,...Ch. 13.2 - List all the combinationss of 5 objects a , b , c...Ch. 13.2 - List all the combinations of 4 objects 1, 2, 3,...Ch. 13.2 - List all the combinationss of 6 objects 1, 2, 3,...Ch. 13.2 - Forming Codes How many two-letter codes can be...Ch. 13.2 - Forming Codes How many two-letter codes can be...Ch. 13.2 - Forming Numbers How many three-digit numbers can...Ch. 13.2 - Forming Numbers How many three-digit numbers can...Ch. 13.2 - Lining People Up In how many ways can 4 people be...Ch. 13.2 - Stacking Boxes In how many ways can 5 different...Ch. 13.2 - Forming Codes How many different three-letter...Ch. 13.2 - Forming Codes How many different four-letter codes...Ch. 13.2 - Stocks on the NYSE Companies whose stocks are...Ch. 13.2 - Stocks on the NASDAQ Companies whose stocks are...Ch. 13.2 - Establishing Committees In how many ways can a...Ch. 13.2 - Establishing Committees In how many ways can a...Ch. 13.2 - Possible Answers on a True/False Test How many...Ch. 13.2 - Possible Answers on a Multiple-choice Test How...Ch. 13.2 - Arranging Books Five different mathematics books...Ch. 13.2 - Prob. 46AYUCh. 13.2 - Birthday Problem In how many ways can 2 people...Ch. 13.2 - Prob. 48AYUCh. 13.2 - Prob. 49AYUCh. 13.2 - Prob. 50AYUCh. 13.2 - Forming Words How many different 9-letter words...Ch. 13.2 - Prob. 52AYUCh. 13.2 - Selecting Objects An urn contains 7 white balls...Ch. 13.2 - Prob. 54AYUCh. 13.2 - Prob. 55AYUCh. 13.2 - Prob. 56AYUCh. 13.2 - Prob. 57AYUCh. 13.2 - Prob. 58AYUCh. 13.2 - Prob. 59AYUCh. 13.2 - Prob. 60AYUCh. 13.2 - Prob. 61AYUCh. 13.2 - Prob. 62AYUCh. 13.2 - Combination Locks A combination lock displays 50...Ch. 13.2 - Prob. 64AYUCh. 13.2 - Prob. 65AYUCh. 13.2 - Prob. 66AYUCh. 13.3 - When the same probability is assigned to each...Ch. 13.3 - Prob. 2AYUCh. 13.3 - Prob. 3AYUCh. 13.3 - Prob. 4AYUCh. 13.3 - In a probability model, which of the following...Ch. 13.3 - Prob. 6AYUCh. 13.3 - Determine whether the following is a probability...Ch. 13.3 - Prob. 8AYUCh. 13.3 - Prob. 9AYUCh. 13.3 - Prob. 10AYUCh. 13.3 - In Problems 11-16, construct a probability model...Ch. 13.3 - In Problems 11-16, construct a probability model...Ch. 13.3 - In Problems 11-16, construct a probability model...Ch. 13.3 - Prob. 14AYUCh. 13.3 - In Problems 11-16, construct a probability model...Ch. 13.3 - In Problems 11-16, construct a probability model...Ch. 13.3 - In Problems 17-22, use the following spinners to...Ch. 13.3 - In Problems 17-22, use the following spinners to...Ch. 13.3 - In Problems 17-22, use the following spinners to...Ch. 13.3 - In Problems 17-22, use the following spinners to...Ch. 13.3 - In Problems 17-22, use the following spinners to...Ch. 13.3 - In Problems 17-22, use the following spinners to...Ch. 13.3 - In Problems 23-26, consider the experiment of...Ch. 13.3 - In Problems 23-26, consider the experiment of...Ch. 13.3 - Prob. 25AYUCh. 13.3 - Prob. 26AYUCh. 13.3 - Assigning Probabilities A coin is weighted so that...Ch. 13.3 - Assigning Probabilities A coin is weighted so that...Ch. 13.3 - Assigning Probabilities A die is weighted so that...Ch. 13.3 - Assigning Probabilities A die is weighted so that...Ch. 13.3 - For Problems 31-34, the sample space is S={...Ch. 13.3 - For Problems 31-34, the sample space is S={...Ch. 13.3 - For Problems 31-34, the sample space is S={...Ch. 13.3 - For Problems 31-34, the sample space is S={...Ch. 13.3 - For Problems 35 and 36, an urn contains 5 white...Ch. 13.3 - For Problems 35 and 36, an urn contains 5 white...Ch. 13.3 - In Problems 37-40, assume equally likely outcomes....Ch. 13.3 - In Problems 37-40, assume equally likely outcomes....Ch. 13.3 - In Problems 37-40, assume equally likely outcomes....Ch. 13.3 - In Problems 37-40, assume equally likely outcomes....Ch. 13.3 - Prob. 41AYUCh. 13.3 - Prob. 42AYUCh. 13.3 - Prob. 43AYUCh. 13.3 - Prob. 45AYUCh. 13.3 - In Problems 45-48, find the probability of the...Ch. 13.3 - Prob. 47AYUCh. 13.3 - Prob. 48AYUCh. 13.3 - Prob. 49AYUCh. 13.3 - Prob. 50AYUCh. 13.3 - Automobile Theft According to the Insurance...Ch. 13.3 - Prob. 52AYUCh. 13.3 - Cat Ownership According to the American Pet...Ch. 13.3 - Doctorate Degrees According to the National...Ch. 13.3 - Prob. 55AYUCh. 13.3 - Prob. 56AYUCh. 13.3 - Prob. 57AYUCh. 13.3 - Prob. 58AYUCh. 13.3 - Prob. 59AYUCh. 13.3 - Prob. 60AYUCh. 13.3 - Prob. 61AYUCh. 13.3 - Prob. 62AYUCh. 13.3 - Prob. 63AYUCh. 13.3 - Prob. 64AYUCh. 13.3 - Prob. 65AYUCh. 13.3 - Prob. 66AYUCh. 13.3 - Surveys In a survey about the number of TV sets in...Ch. 13.3 - Prob. 68AYUCh. 13.3 - Prob. 69AYUCh. 13.3 - Prob. 70AYUCh. 13.3 - Prob. 71AYUCh. 13.3 - Prob. 72AYUCh. 13.3 - Prob. 73AYUCh. 13 - Prob. 1RECh. 13 - Prob. 2RECh. 13 - Prob. 3RECh. 13 - Prob. 4RECh. 13 - Prob. 5RECh. 13 - Prob. 6RECh. 13 - Prob. 7RECh. 13 - Prob. 8RECh. 13 - Prob. 9RECh. 13 - Prob. 10RECh. 13 - Prob. 11RECh. 13 - Prob. 12RECh. 13 - Prob. 13RECh. 13 - Prob. 14RECh. 13 - Prob. 15RECh. 13 - Prob. 16RECh. 13 - Prob. 17RECh. 13 - Prob. 18RECh. 13 - Prob. 19RECh. 13 - Prob. 20RECh. 13 - Prob. 21RECh. 13 - Prob. 22RECh. 13 - Prob. 23RECh. 13 - Prob. 24RECh. 13 - Prob. 25RECh. 13 - Prob. 26RECh. 13 - Prob. 27RECh. 13 - Prob. 28RECh. 13 - Prob. 29RECh. 13 - Prob. 30RECh. 13 - Prob. 31RECh. 13 - Prob. 32RECh. 13 - Prob. 33RECh. 13 - Prob. 34RECh. 13 - Prob. 35RECh. 13 - Prob. 36RECh. 13 - Prob. 37RECh. 13 - Prob. 38RECh. 13 - Prob. 39RECh. 13 - Prob. 40RECh. 13 - Prob. 1CTCh. 13 - In Problems, a survey of college freshmen asked...Ch. 13 - In Problems 14, a survey of 70college freshmen...Ch. 13 - In Problems 14, a survey of 70college freshmen...Ch. 13 - Prob. 5CTCh. 13 - Prob. 6CTCh. 13 - Prob. 7CTCh. 13 - MMs offers customers the opportunity to create...Ch. 13 - Prob. 9CTCh. 13 - Prob. 10CTCh. 13 - On February 20, 2004, the Ohio Bureau of Motor...Ch. 13 - Kiersten applies for admission to the University...Ch. 13 - A cooler contains 8 bottles of Pepsi, 5 bottles of...Ch. 13 - Prob. 14CTCh. 13 - Prob. 15CTCh. 13 - Prob. 16CTCh. 13 - Prob. 1CRCh. 13 - Prob. 2CRCh. 13 - Prob. 3CRCh. 13 - Prob. 4CRCh. 13 - Prob. 5CRCh. 13 - Prob. 6CRCh. 13 - Prob. 7CRCh. 13 - Prob. 8CRCh. 13 - Prob. 9CRCh. 13 - Prob. 10CRCh. 13 - Graph: y=3sin(2x+)Ch. 13 - Prob. 12CR
Additional Math Textbook Solutions
Find more solutions based on key concepts
True or False? In Exercises 5–8, determine whether the statement is true or false. If it is false, rewrite it a...
Elementary Statistics: Picturing the World (7th Edition)
Identify f as being linear, quadratic, or neither. If f is quadratic, identify the leading coefficient a and ...
College Algebra with Modeling & Visualization (5th Edition)
Combining rules Use the Chain Rule combined with other differentiation rules to find the derivative of the foll...
Calculus: Early Transcendentals (2nd Edition)
If n is a counting number, bn, read______, indicates that there are n factors of b. The number b is called the_...
Algebra and Trigonometry (6th Edition)
The four flaws in the given survey.
Elementary Statistics
Knowledge Booster
Similar questions
- water at a rate of 2 m³/min. of the water height in this tank? 16) A box with a square base and an open top must have a volume of 256 cubic inches. Find the dimensions of the box that will minimize the amount of material used (the surface area). 17) A farmer wishes toarrow_forward#14 Sand pours from a chute and forms a conical pile whose height is always equal to its base diameter. The height o the pile increases at a rate of 5 feet/hour. Find the rate of change of the volume of the sand in the conical pile when the height of the pile is 4 feet.arrow_forward(d)(65in(x)-5 cos(x) dx mins by 5x-2x² 3x+1 dx -dx 20 Evaluate each the following indefinite integralsarrow_forward
- 19 Evaluate each the following definite integrals: a) લ b) (+3) 6) (2-2)(+33) dxarrow_forward#11 If a snowball melts so its surface area decreases at a rate of 1cm²/min, find the rate at which the diameter decreases when the diameter is 6 cm.arrow_forwardUse Deritivitve of the inverse to solve thisarrow_forward
- Evaluate the following Limits: e6x-1 Lim +0Sin3x 7x-5x2 2x-1+ Cos 4x +6 c) Lim b) Lim + x³-x2 X-0 1-e' 4x d) Lim 6x²-3 X+0 6x+2x² Find the derivatives of the following functions using the Limit definition of derivativearrow_forward15A cylindrical tank with radius 8 m is being filled with water at a rate of 2 m³/min. What is the rate of change of the water height in this tank? 6)A box with a square base and an open top must box that will minimiarrow_forward#12 The radius of a sphere increases at a rate of 3 in/sec. How fast is the volume increasing when the diameter is 24arrow_forward
- 84 256 cubic inches. Find the dimensions of the of material used (the surface area). A farmer wishes to enclose a rectangular plot using 200 m of fencing material. One side of the land borders a river and does not need fencing. What is the largest area that can be enclosed? For the function y=x³-3x²-1, use derivatives to: 3 b) 2x - 6x2 (a) determine the intarrow_forwardCan you solve this 6 questions numerical method and teach me how to solve it and what we use.arrow_forward9Wire of length 20m is divided into two pieces and the pieces are bent into a square and a circle. How should this be done in order to minimize the sum of their areas? Round your answer to the nearest hundredth.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning