
Each edge of a cubical box has length 1 m. The box contains nine spherical balls with the same radius r. The center of one ball is at the center of the cube and it touches the other eight balls. Each of the other eight balls touches three sides of the box. Thus the balls are tightly packed in the box (see the figure). Find r. (If you have trouble with this problem, read about the problem-solving strategy entitled Use Analogy on page 98.)
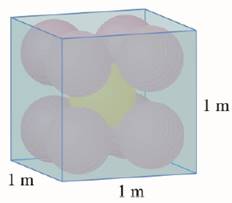
To find:
The radius r
Answer to Problem 1P
Solution:
The radius of each ball is
r =√3-32m
Explanation of Solution
1) Concept:
We create an analogous problem in two dimensions and use the strategy in two dimension to solve the problem in three dimension.
2) Calculation:
Since three dimensional situations are often diffucult to visualize and work with, we create an analogous problem in two dimensions and use the strategy in two dimension to solve the problem in three dimension.
Let us try to find the analogous problem in two dimensions. The analogue of a cube is a square, and the analogue of a sphere is a circle.Thus, a simillar problem in two dimensions is as follows:
What is r, if five circles with the same radius r are contained in a square of side 1m so that the circles touch each other and four of the circles touch two sides of square, as shown in the figure,
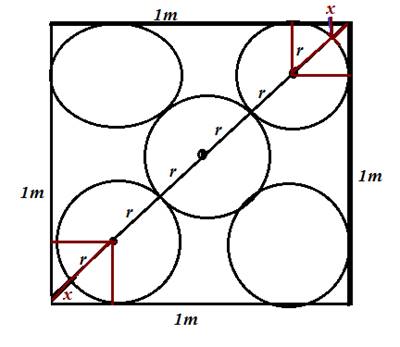
By pythagorean Theorem, the diagonal of the square is √2
Also from the figure, the diagonal of the square is 4r+2x
Therefore, 4r+2x=√2
But, x is the diagonal of the smallar square of side r.
Therefore,
x=√2 r
Therefore,
4r+2x=√2 implies that
4r+2√2 r =√2
That is, (4+2√2) r =√2
Therefore,
r =√2(4+2√2)
Let’s use this idea to solve the original three dimensional problem.
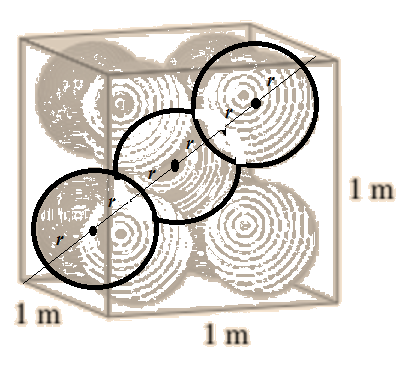
The diagonal of the cube is √12+12+12=√3
And the diagonal of the cube is also 4r+2x.
Therefore, 4r+2x=√3
where x is the diagonal of the cube with edge r.
Therefore,
x=√r2+r2+r2=√3 r
Therefore,
4r+2x=√3 implies that 4r+2√3 r=√3
That is, (4+2 √3) r =√3
Therefore,
r =√3(4+2√3)
By rationalization,
r =2√3-32
Therefore, the radius of each ball is
r =√3-32m
Conclusion:
The radius of each ball is
r =√3-32m
Want to see more full solutions like this?
Chapter 12 Solutions
Bundle: Calculus, 8th + Enhanced WebAssign - Start Smart Guide for Students + WebAssign Printed Access Card for Stewart's Calculus, 8th Edition, Multi-Term
- (14 points) Let f: R3 R and T: R3. →R³ be defined by f(x, y, z) = ln(x²+ y²+2²), T(p, 0,4)=(psin cos 0, psin sin, pcos). (a) (4 points) Write out the composition g(p, 0, 4) = (foT)(p,, ) explicitly. Then calculate the gradient Vg directly, i.e. without using the chain rule. (b) (4 points) Calculate the gradient Vf(x, y, z) where (x, y, z) = T(p, 0,4). (c) (6 points) Calculate the derivative matrix DT(p, 0, p). Then use the Chain Rule to calculate Vg(r,0,4).arrow_forward(10 points) Let S be the upper hemisphere of the unit sphere x² + y²+2² = 1. Let F(x, y, z) = (x, y, z). Calculate the surface integral J F F-dS. Sarrow_forward(8 points) Calculate the following line integrals. (a) (4 points) F Fds where F(x, y, z) = (x, y, xy) and c(t) = (cost, sint, t), tЄ [0,π] . (b) (4 points) F. Fds where F(x, y, z) = (√xy, e³, xz) where c(t) = (t², t², t), t = [0, 1] .arrow_forward
- review help please and thank you!arrow_forward(10 points) Let S be the surface that is part of the sphere x² + y²+z² = 4 lying below the plane 2√3 and above the plane z-v -√3. Calculate the surface area of S.arrow_forward(8 points) Let D = {(x, y) | 0 ≤ x² + y² ≤4}. Calculate == (x² + y²)³/2dA by making a change of variables to polar coordinates, i.e. x=rcos 0, y = r sin 0.arrow_forward
- x² - y² (10 points) Let f(x,y): = (a) (6 points) For each vector u = (1, 2), calculate the directional derivative Duƒ(1,1). (b) (4 points) Determine all unit vectors u for which Duf(1, 1) = 0.arrow_forwardSolve : X + sin x = 0. By the false positioning numerical methodarrow_forwardSolve: X + sin X = 0 by the false positionining numerical methodarrow_forward
- On from the equation: 2 u = C₁ + C₂ Y + Czy + Cu y³ Find C₁, C₂, C3 and Cy Using these following Cases : (a) 4=0 at y=0 (b) U = U∞ at y = 8 du (c) at Y = S ду --y. ди = 0 at y = 0 бугarrow_forwardTips S ps L 50. lim x2 - 4 x-2x+2 51. lim 22 - X 52. 53. x 0 Answer lim x 0 lim 2-5 X 2x2 2 x² Answer -> 54. lim T - 3x - - 25 +5 b+1 b3b+3 55. lim X x-1 x 1 Answer 56. lim x+2 x 2 x 2 57. lim x²-x-6 x-2 x²+x-2 Answer-> 23-8 58. lim 2-22-2arrow_forwardS 36. lim 5x+2 x-2 37. lim √√2x4 + x² x-3 Answer-> 2x3 +4 38. lim x12 √ x² + 1 √√x² + 8 39. lim x-1 2x+4 Answer 40. lim x3 2x x√x² + 7 √√2x+3arrow_forward

 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill





