
Chebyshev’s Theorem How can you determine whether a distribution is approximately normal? A statistical theorem called Chebyshev’s theorem states that the minimum percent of data between plus and minus K standard deviations from the mean (K > 1) in any distribution can be found by the formula
Minimum percent =
Thus, for example, between ±2 standard deviations from the mean there will always be a minimum of 75% of data. This minimum percent applies to any distribution For K = 2,
Minimum percent
Likewise, between ±3 standard deviations from the mean there will always be a minimum of 89% of the data. For K = 3,
Minimum percent
The following table lists the minimum percent of data in any distribution and the actual percent of data in the normal distribution between ±1.1, ± 1.5, ± 2.0, and ±2.5 standard deviations from the mean. The minimum percents of data m any distribution were calculated by using Chebyshev’s theorem. The actual percents of data for the normal distribution were calculated by using the area given in the standard normal, or z, table.
| K = 1.1 | K = 1.5 | K = 2 | K = 2.5 | |
| Minimum (for any distribution) | 17.4% | 55.6% | 75% | 84% |
| Normal distribution | 72.9% | 86.6% | 95.4% | 98.8% |
| Given distribution |
The third row of the chart has been left blank for you to fill in the percents when you reach part (e).
Consider the following 30 pieces of data obtained from a quiz.
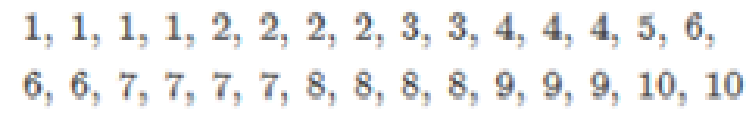
- a. Determine the mean of the set of scores.
- b. Determine the standard deviation of the set of scores.
- c. Determine the values that correspond to 1.1, 1.5, 2, and 2.5 standard deviations above the mean. Then determine the values that correspond to 1.1, 1.5, 2, and 2. 5 standard deviations below the mean.
- d. By observing the 30 pieces of data, determine the actual percent of quiz scores between
±1.1 standard deviations from the mean.
±1.5 standard deviations from the mean.
±2 tandard deviations from the mean.
±2.5 standard deviations from the mean.
- e. Place the percents found in part (d) in the third row of the chart.
- f. Compare the percents in the third row of the chart with the minimum percents in the first row and the normal percents in the second row, and then make a judgment as to whether this set of 30 scores is approximately
normally distributed .
Want to see the full answer?
Check out a sample textbook solution
Chapter 12 Solutions
A Survey of Mathematics with Applications Plus MyLab Math with Pearson eText -- 18 Week Access Card Package
- 10-2 Let A = 02-4 and b = 4 Denote the columns of A by a₁, a2, a3, and let W = Span {a1, a2, a̸3}. -4 6 5 - 35 a. Is b in {a1, a2, a3}? How many vectors are in {a₁, a₂, a3}? b. Is b in W? How many vectors are in W? c. Show that a2 is in W. [Hint: Row operations are unnecessary.] a. Is b in {a₁, a2, a3}? Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. ○ A. No, b is not in {a₁, a2, 3} since it cannot be generated by a linear combination of a₁, a2, and a3. B. No, b is not in (a1, a2, a3} since b is not equal to a₁, a2, or a3. C. Yes, b is in (a1, a2, a3} since b = a (Type a whole number.) D. Yes, b is in (a1, a2, 3} since, although b is not equal to a₁, a2, or a3, it can be expressed as a linear combination of them. In particular, b = + + ☐ az. (Simplify your answers.)arrow_forward(1) (14 points) Let a = (-2, 10, -4) and b = (3, 1, 1). (a) (4 points) Using the dot product determine the angle between a and b. (b) (2 points) Determine the cross product vector axb. (c) (4 points) Calculate the area of the parallelogram spanned by a and b. Justify your answer. 1arrow_forward(d) (4 points) Think of this sheet of paper as the plane containing the vectors a = (1,1,0) and b = (2,0,0). Sketch the parallelogram P spanned by a and b. Which diagonal of P represents the vector ab geometrically? d be .dx adjarrow_forward
- 2) Based on the given information and the diagram, a. Which congruence statements can be proven? Select all that apply.Given: Overline OR is congruent to overline OQ, angle N is congruent to angle PProve: angle 3 is congruent to angle 5A. Overline ON is congruent to overline OPB. Angle 1 is congruent to angle 2C. Overline ON is congruent to overline OR and overline OP is congruent to overine OQD. angle 1 is congruent to angle 3 and angle 2 is congruent to angle 5There are more than one correct answerarrow_forward(2) (4 points) Find all vectors v having length 1 that are perpendicular to both =(2,0,2) and j = (0,1,0). Show all work. a=arrow_forwardNo chatgpt pls will upvotearrow_forward
- Title: Analyzing Customer Satisfaction for UnileverAs a member of Unilever's Customer Experience Management team, you are responsible forevaluating customer satisfaction levels and monitoring competitive moves. This case studyinvolves analyzing satisfaction data to test two key hypotheses about Unilever's performancerelative to its main competitor, Procter & Gamble (P&G).Unilever’s leadership team has emphasized the importance of customer satisfaction inmaintaining competitive advantage and market leadership. As part of this initiative, yourteam regularly monitors satisfaction scores and benchmarks them against competitors likeP&G.You are tasked with analyzing the provided dataset to answer the following questions:1. Does Unilever’s average customer satisfaction score meet the minimum threshold of2. 75%?Is there no significant difference between Unilever’s overall average satisfaction scoreand P&G’s average satisfaction score?arrow_forwardPlease help me first one graphically and the other in matrixarrow_forwardPlease help me with this in matrix pleasearrow_forward
- Please solve the differential geometry problem No chatgpt pls will upvote.arrow_forwardQ1. A group of five applicants for a pair of identical jobs consists of three men and two women. The employer is to select two of the five applicants for the jobs. Let S denote the set of all possible outcomes for the employer's selection. Let A denote the subset of outcomes corresponding to the selection of two men and B the subset corresponding to the selection of at least one woman. List the outcomes in A, B, AUB, AN B, and An B. (Denote the different men and women by M₁, M2, M3 and W₁, W2, respectively.)arrow_forwardFor the following function, find the full power series centered at a of convergence. 0 and then give the first 5 nonzero terms of the power series and the open interval = f(2) Σ 8 1(x)--(-1)*(3)* n=0 ₤(x) = + + + ++... The open interval of convergence is: 1 1 3 f(x)= = 28 3x6 +1 (Give your answer in help (intervals) .)arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt

